Fair in the Eyes of Others
Paper and Code
Nov 25, 2019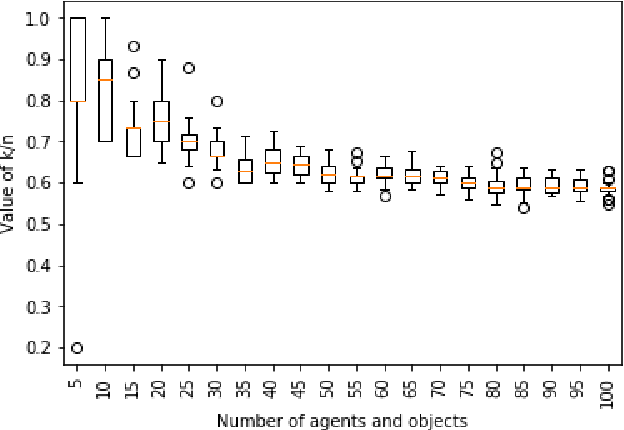

Envy-freeness is a widely studied notion in resource allocation, capturing some aspects of fairness. The notion of envy being inherently subjective though, it might be the case that an agent envies another agent, but that she objectively has no reason to do so. The difficulty here is to define the notion of objectivity, since no ground-truth can properly serve as a basis of this definition. A natural approach is to consider the judgement of the other agents as a proxy for objectivity. Building on previous work by Parijs (who introduced "unanimous envy") we propose the notion of approval envy: an agent $a_i$ experiences approval envy towards $a_j$ if she is envious of $a_j$, and sufficiently many agents agree that this should be the case, from their own perspectives. Some interesting properties of this notion are put forward. Computing the minimal threshold guaranteeing approval envy clearly inherits well-known intractable results from envy-freeness, but (i) we identify some tractable cases such as house allocation; and (ii) we provide a general method based on a mixed integer programming encoding of the problem, which proves to be efficient in practice. This allows us in particular to show experimentally that existence of such allocations, with a rather small threshold, is very often observed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge