Efficiency and Sequenceability in Fair Division of Indivisible Goods with Additive Preferences
Paper and Code
Apr 06, 2016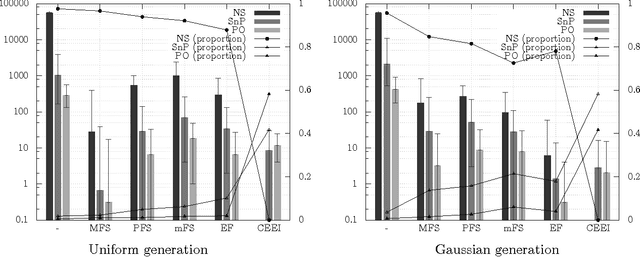
In fair division of indivisible goods, using sequences of sincere choices (or picking sequences) is a natural way to allocate the objects. The idea is the following: at each stage, a designated agent picks one object among those that remain. This paper, restricted to the case where the agents have numerical additive preferences over objects, revisits to some extent the seminal paper by Brams and King [9] which was specific to ordinal and linear order preferences over items. We point out similarities and differences with this latter context. In particular, we show that any Pareto-optimal allocation (under additive preferences) is sequenceable, but that the converse is not true anymore. This asymmetry leads naturally to the definition of a "scale of efficiency" having three steps: Pareto-optimality, sequenceability without Pareto-optimality, and non-sequenceability. Finally, we investigate the links between these efficiency properties and the "scale of fairness" we have described in an earlier work [7]: we first show that an allocation can be envy-free and non-sequenceable, but that every competitive equilibrium with equal incomes is sequenceable. Then we experimentally explore the links between the scales of efficiency and fairness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge