Robust Ordinal Regression for Subsets Comparisons with Interactions

This paper is dedicated to a robust ordinal method for learning the preferences of a decision maker between subsets. The decision model, derived from Fishburn and LaValle (1996) and whose parameters we learn, is general enough to be compatible with any strict weak order on subsets, thanks to the consideration of possible interactions between elements. Moreover, we accept not to predict some preferences if the available preference data are not compatible with a reliable prediction. A predicted preference is considered reliable if all the simplest models (Occam's razor) explaining the preference data agree on it. Following the robust ordinal regression methodology, our predictions are based on an uncertainty set encompassing the possible values of the model parameters. We define a robust ordinal dominance relation between subsets and we design a procedure to determine whether this dominance relation holds. Numerical tests are provided on synthetic and real-world data to evaluate the richness and reliability of the preference predictions made.

Cautious Learning of Multiattribute Preferences

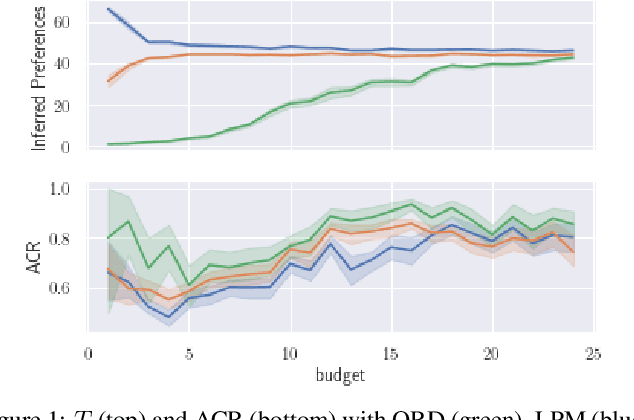
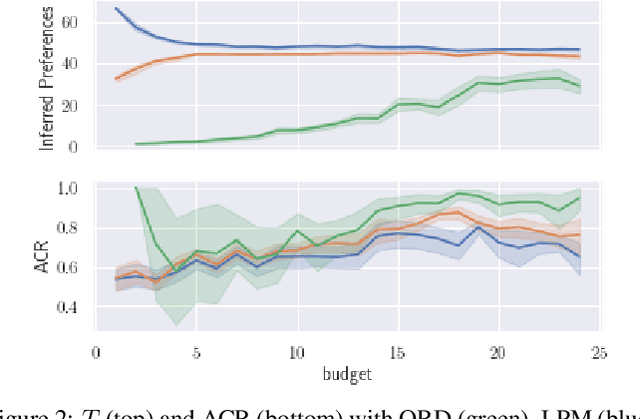
This paper is dedicated to a cautious learning methodology for predicting preferences between alternatives characterized by binary attributes (formally, each alternative is seen as a subset of attributes). By "cautious", we mean that the model learned to represent the multi-attribute preferences is general enough to be compatible with any strict weak order on the alternatives, and that we allow ourselves not to predict some preferences if the data collected are not compatible with a reliable prediction. A predicted preference will be considered reliable if all the simplest models (following Occam's razor principle) explaining the training data agree on it. Predictions are based on an ordinal dominance relation between alternatives [Fishburn and LaValle, 1996]. The dominance relation relies on an uncertainty set encompassing the possible values of the parameters of the multi-attribute utility function. Numerical tests are provided to evaluate the richness and the reliability of the predictions made.