Online 2-stage Stable Matching

We focus on an online 2-stage problem, motivated by the following situation: consider a system where students shall be assigned to universities. There is a first round where some students apply, and a first (stable) matching $M_1$ has to be computed. However, some students may decide to leave the system (change their plan, go to a foreign university, or to some institution not in the system). Then, in a second round (after these deletions), we shall compute a second (final) stable matching $M_2$. As it is undesirable to change assignments, the goal is to minimize the number of divorces/modifications between the two stable matchings $M_1$ and $M_2$. Then, how should we choose $M_1$ and $M_2$? We show that there is an {\it optimal online} algorithm to solve this problem. In particular, thanks to a dominance property, we show that we can optimally compute $M_1$ without knowing the students that will leave the system. We generalize the result to some other possible modifications in the input (students, open positions). We also tackle the case of more stages, showing that no competitive (online) algorithm can be achieved for the considered problem as soon as there are 3 stages.

Kemeny ranking is NP-hard for 2-dimensional Euclidean preferences

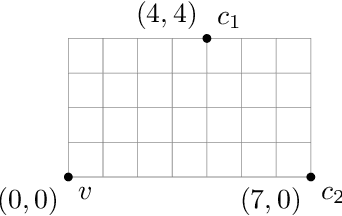
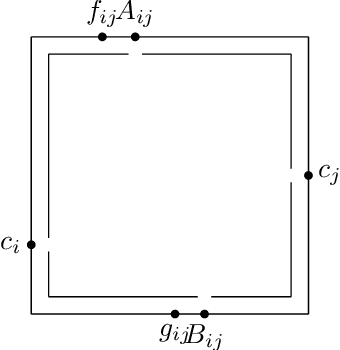
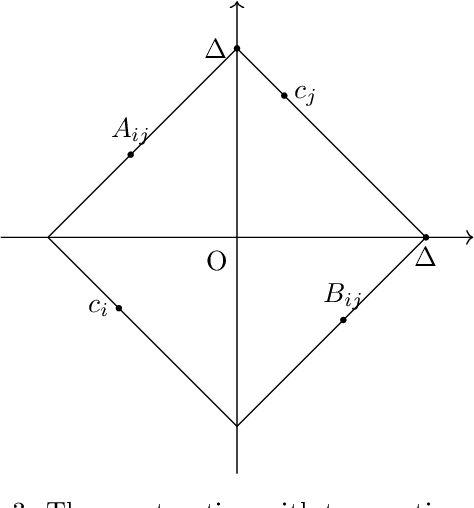
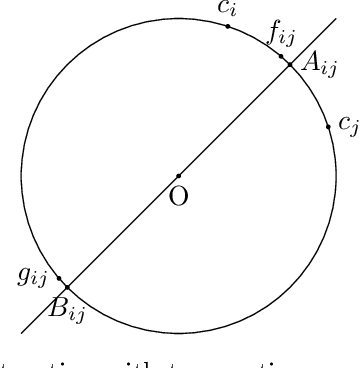
The assumption that voters' preferences share some common structure is a standard way to circumvent NP-hardness results in social choice problems. While the Kemeny ranking problem is NP-hard in the general case, it is known to become easy if the preferences are 1-dimensional Euclidean. In this note, we prove that the Kemeny ranking problem is NP-hard for d-dimensional Euclidean preferences with d>=2. We note that this result also holds for the Slater ranking problem.

Online-Learning for min-max discrete problems

We study various discrete nonlinear combinatorial optimization problems in an online learning framework. In the first part, we address the question of whether there are negative results showing that getting a vanishing (or even vanishing approximate) regret is computational hard. We provide a general reduction showing that many (min-max) polynomial time solvable problems not only do not have a vanishing regret, but also no vanishing approximation $\alpha$-regret, for some $\alpha$ (unless $NP=BPP$). Then, we focus on a particular min-max problem, the min-max version of the vertex cover problem which is solvable in polynomial time in the offline case. The previous reduction proves that there is no $(2-\epsilon)$-regret online algorithm, unless Unique Game is in $BPP$; we prove a matching upper bound providing an online algorithm based on the online gradient descent method. Then, we turn our attention to online learning algorithms that are based on an offline optimization oracle that, given a set of instances of the problem, is able to compute the optimum static solution. We show that for different nonlinear discrete optimization problems, it is strongly $NP$-hard to solve the offline optimization oracle, even for problems that can be solved in polynomial time in the static case (e.g. min-max vertex cover, min-max perfect matching, etc.). On the positive side, we present an online algorithm with vanishing regret that is based on the follow the perturbed leader algorithm for a generalized knapsack problem.

The Convergence of Iterative Delegations in Liquid Democracy in a Social Network

Liquid democracy is a collective decision making paradigm which lies between direct and representative democracy. One of its main features is that voters can delegate their votes in a transitive manner such that: A delegates to B and B delegates to C leads to A indirectly delegates to C. These delegations can be effectively empowered by implementing liquid democracy in a social network, so that voters can delegate their votes to any of their neighbors in the network. However, it is uncertain that such a delegation process will lead to a stable state where all voters are satisfied with the people representing them. We study the stability (w.r.t. voters preferences) of the delegation process in liquid democracy and model it as a game in which the players are the voters and the strategies are their possible delegations. We answer several questions on the equilibria of this process in any social network or in social networks that correspond to restricted types of graphs. We show that a Nash-equilibrium may not exist, and that it is even NP-complete to decide whether one exists or not. This holds even if the social network is a complete graph or a bounded degree graph. We further show that this existence problem is W[1]-hard w.r.t. the treewidth of the social network. Besides these hardness results, we demonstrate that an equilibrium always exists whatever the preferences of the voters iff the social network is a tree. We design a dynamic programming procedure to determine some desirable equilibria (e.g., minimizing the dissatisfaction of the voters) in polynomial time for tree social networks. Lastly, we study the convergence of delegation dynamics. Unfortunately, when an equilibrium exists, we show that a best response dynamics may not converge, even if the social network is a path or a complete graph.

The Convergence of Iterative Delegations in Liquid Democracy

In this paper, we study liquid democracy, a collective decision making paradigm which lies between direct and representative democracy. One main feature of liquid democracy is that voters can delegate their votes in a transitive manner such that: A delegates to B and B delegates to C leads to A delegates to C. We study the stability (w.r.t. voters preferences) of the delegation process in liquid democracy and model it as a game in which the players are the voters and the strategies are possible delegations. This game-theoretic model enables us to answer several questions on the equilibria of this process under general preferences and several types of restricted preferences (e.g., single-peaked preferences).