Primal-Dual Algorithms with Predictions for Online Bounded Allocation and Ad-Auctions Problems

Matching problems have been widely studied in the research community, especially Ad-Auctions with many applications ranging from network design to advertising. Following the various advancements in machine learning, one natural question is whether classical algorithms can benefit from machine learning and obtain better-quality solutions. Even a small percentage of performance improvement in matching problems could result in significant gains for the studied use cases. For example, the network throughput or the revenue of Ad-Auctions can increase remarkably. This paper presents algorithms with machine learning predictions for the Online Bounded Allocation and the Online Ad-Auctions problems. We constructed primal-dual algorithms that achieve competitive performance depending on the quality of the predictions. When the predictions are accurate, the algorithms' performance surpasses previous performance bounds, while when the predictions are misleading, the algorithms maintain standard worst-case performance guarantees. We provide supporting experiments on generated data for our theoretical findings.

Handling Delayed Feedback in Distributed Online Optimization : A Projection-Free Approach

Learning at the edges has become increasingly important as large quantities of data are continually generated locally. Among others, this paradigm requires algorithms that are simple (so that they can be executed by local devices), robust (again uncertainty as data are continually generated), and reliable in a distributed manner under network issues, especially delays. In this study, we investigate the problem of online convex optimization under adversarial delayed feedback. We propose two projection-free algorithms for centralised and distributed settings in which they are carefully designed to achieve a regret bound of O(\sqrt{B}) where B is the sum of delay, which is optimal for the OCO problem in the delay setting while still being projection-free. We provide an extensive theoretical study and experimentally validate the performance of our algorithms by comparing them with existing ones on real-world problems.

One Gradient Frank-Wolfe for Decentralized Online Convex and Submodular Optimization

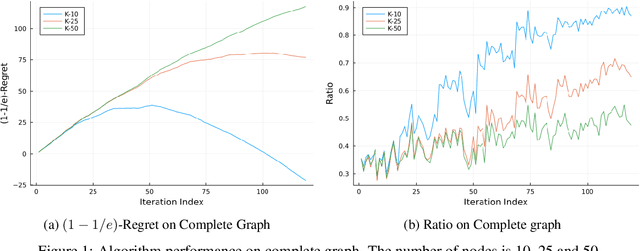
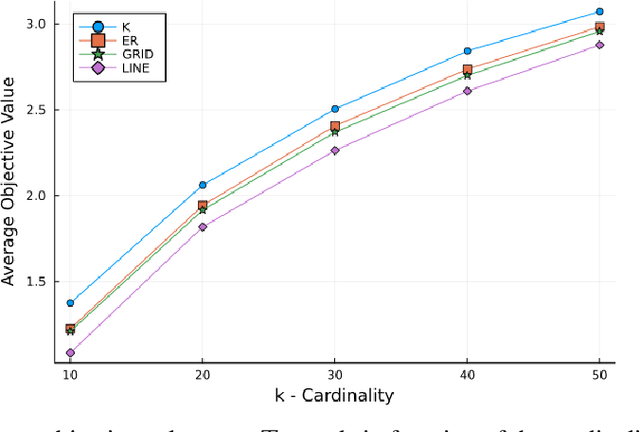
Decentralized learning has been studied intensively in recent years motivated by its wide applications in the context of federated learning. The majority of previous research focuses on the offline setting in which the objective function is static. However, the offline setting becomes unrealistic in numerous machine learning applications that witness the change of massive data. In this paper, we propose \emph{decentralized online} algorithm for convex and continuous DR-submodular optimization, two classes of functions that are present in a variety of machine learning problems. Our algorithms achieve performance guarantees comparable to those in the centralized offline setting. Moreover, on average, each participant performs only a \emph{single} gradient computation per time step. Subsequently, we extend our algorithms to the bandit setting. Finally, we illustrate the competitive performance of our algorithms in real-world experiments.

Online Decentralized Frank-Wolfe: From theoretical bound to applications in smart-building

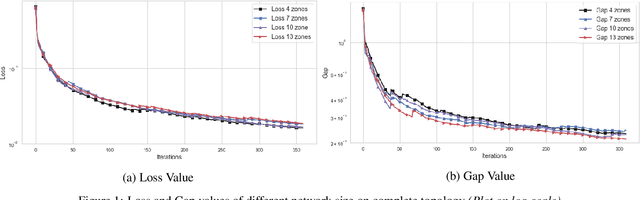
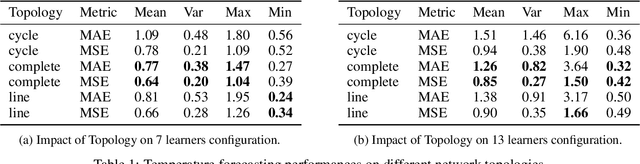
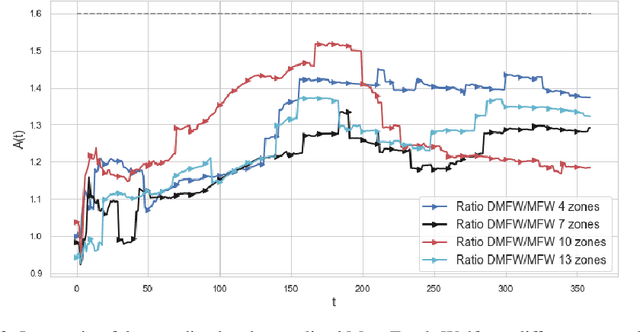
The design of decentralized learning algorithms is important in the fast-growing world in which data are distributed over participants with limited local computation resources and communication. In this direction, we propose an online algorithm minimizing non-convex loss functions aggregated from individual data/models distributed over a network. We provide the theoretical performance guarantee of our algorithm and demonstrate its utility on a real life smart building.

Online Primal-Dual Algorithms with Predictions for Packing Problems

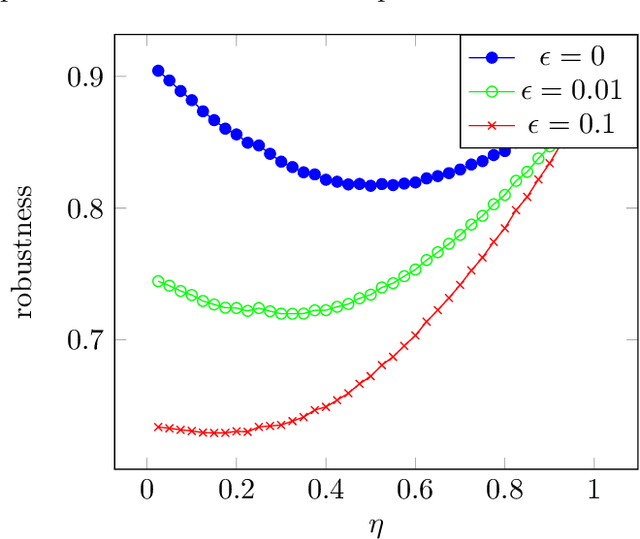
The domain of online algorithms with predictions has been extensively studied for different applications such as scheduling, caching (paging), clustering, ski rental, etc. Recently, Bamas et al., aiming for an unified method, have provided a primal-dual framework for linear covering problems. They extended the online primal-dual method by incorporating predictions in order to achieve a performance beyond the worst-case case analysis. In this paper, we consider this research line and present a framework to design algorithms with predictions for non-linear packing problems. We illustrate the applicability of our framework in submodular maximization and in particular ad-auction maximization in which the optimal bound is given and supporting experiments are provided.

Online Non-Monotone DR-submodular Maximization

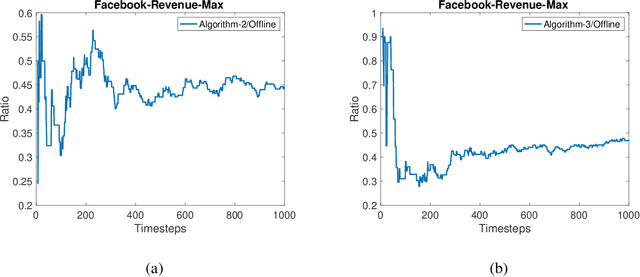
In this paper, we study problems at the interface of two important fields: \emph{submodular optimization} and \emph{online learning}. Submodular functions play a vital role in modelling cost functions that naturally arise in many areas of discrete optimization. These functions have been studied under various models of computation. Independently, submodularity has been considered in continuous domains. In fact, many problems arising in machine learning and statistics have been modelled using continuous DR-submodular functions. In this work, we are study the problem of maximizing \textit{non-monotone} continuous DR-submodular functions within the framework of online learning. We provide three main results. First, we present an online algorithm (in full-information setting) that achieves an approximation guarantee (depending on the search space) for the problem of maximizing non-monotone continuous DR-submodular functions over a \emph{general} convex domain. To best of our knowledge, no prior approximation algorithm in full-information setting was known for the non-monotone continuous DR submodular functions even for the \emph{down-closed} convex domain. Second, we show that the online stochastic mirror ascent algorithm (in full information setting) achieves an improved approximation ratio of $(1/4)$ for maximizing the non-monotone continuous DR-submodular functions over a \emph{down-closed} convex domain. At last, we extend our second result to the bandit setting where we present the first approximation guarantee of $(1/4)$. To best of our knowledge, no approximation algorithm for non-monotone submodular maximization was known in the bandit setting.

Online-Learning for min-max discrete problems

We study various discrete nonlinear combinatorial optimization problems in an online learning framework. In the first part, we address the question of whether there are negative results showing that getting a vanishing (or even vanishing approximate) regret is computational hard. We provide a general reduction showing that many (min-max) polynomial time solvable problems not only do not have a vanishing regret, but also no vanishing approximation $\alpha$-regret, for some $\alpha$ (unless $NP=BPP$). Then, we focus on a particular min-max problem, the min-max version of the vertex cover problem which is solvable in polynomial time in the offline case. The previous reduction proves that there is no $(2-\epsilon)$-regret online algorithm, unless Unique Game is in $BPP$; we prove a matching upper bound providing an online algorithm based on the online gradient descent method. Then, we turn our attention to online learning algorithms that are based on an offline optimization oracle that, given a set of instances of the problem, is able to compute the optimum static solution. We show that for different nonlinear discrete optimization problems, it is strongly $NP$-hard to solve the offline optimization oracle, even for problems that can be solved in polynomial time in the static case (e.g. min-max vertex cover, min-max perfect matching, etc.). On the positive side, we present an online algorithm with vanishing regret that is based on the follow the perturbed leader algorithm for a generalized knapsack problem.

Non-monotone DR-submodular Maximization: Approximation and Regret Guarantees

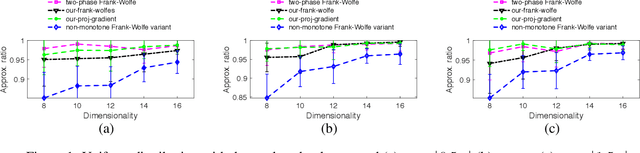
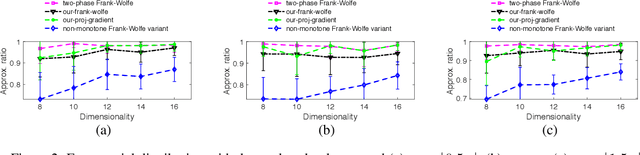
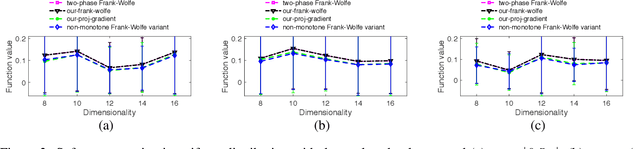
Diminishing-returns (DR) submodular optimization is an important field with many real-world applications in machine learning, economics and communication systems. It captures a subclass of non-convex optimization that provides both practical and theoretical guarantees. In this paper, we study the fundamental problem of maximizing non-monotone DR-submodular functions over down-closed and general convex sets in both offline and online settings. First, we show that for offline maximizing non-monotone DR-submodular functions over a general convex set, the Frank-Wolfe algorithm achieves an approximation guarantee which depends on the convex set. Next, we show that the Stochastic Gradient Ascent algorithm achieves a 1/4-approximation ratio with the regret of $O(1/\sqrt{T})$ for the problem of maximizing non-monotone DR-submodular functions over down-closed convex sets. These are the first approximation guarantees in the corresponding settings. Finally we benchmark these algorithms on problems arising in machine learning domain with the real-world datasets.