Online Non-Monotone DR-submodular Maximization

In this paper, we study problems at the interface of two important fields: \emph{submodular optimization} and \emph{online learning}. Submodular functions play a vital role in modelling cost functions that naturally arise in many areas of discrete optimization. These functions have been studied under various models of computation. Independently, submodularity has been considered in continuous domains. In fact, many problems arising in machine learning and statistics have been modelled using continuous DR-submodular functions. In this work, we are study the problem of maximizing \textit{non-monotone} continuous DR-submodular functions within the framework of online learning. We provide three main results. First, we present an online algorithm (in full-information setting) that achieves an approximation guarantee (depending on the search space) for the problem of maximizing non-monotone continuous DR-submodular functions over a \emph{general} convex domain. To best of our knowledge, no prior approximation algorithm in full-information setting was known for the non-monotone continuous DR submodular functions even for the \emph{down-closed} convex domain. Second, we show that the online stochastic mirror ascent algorithm (in full information setting) achieves an improved approximation ratio of $(1/4)$ for maximizing the non-monotone continuous DR-submodular functions over a \emph{down-closed} convex domain. At last, we extend our second result to the bandit setting where we present the first approximation guarantee of $(1/4)$. To best of our knowledge, no approximation algorithm for non-monotone submodular maximization was known in the bandit setting.

Non-monotone DR-submodular Maximization: Approximation and Regret Guarantees

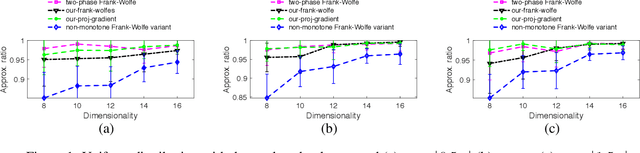
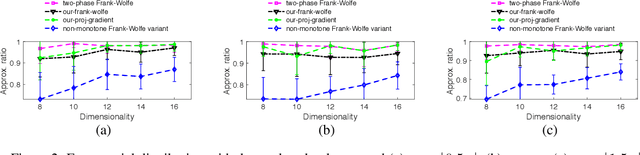
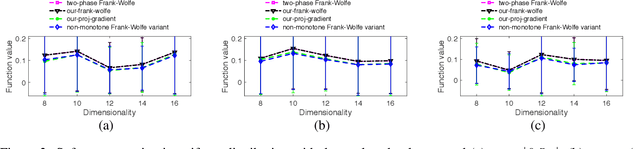
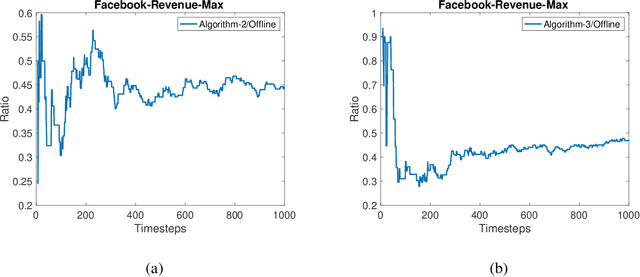
Diminishing-returns (DR) submodular optimization is an important field with many real-world applications in machine learning, economics and communication systems. It captures a subclass of non-convex optimization that provides both practical and theoretical guarantees. In this paper, we study the fundamental problem of maximizing non-monotone DR-submodular functions over down-closed and general convex sets in both offline and online settings. First, we show that for offline maximizing non-monotone DR-submodular functions over a general convex set, the Frank-Wolfe algorithm achieves an approximation guarantee which depends on the convex set. Next, we show that the Stochastic Gradient Ascent algorithm achieves a 1/4-approximation ratio with the regret of $O(1/\sqrt{T})$ for the problem of maximizing non-monotone DR-submodular functions over down-closed convex sets. These are the first approximation guarantees in the corresponding settings. Finally we benchmark these algorithms on problems arising in machine learning domain with the real-world datasets.