Cascading CMA-ES Instances for Generating Input-diverse Solution Batches

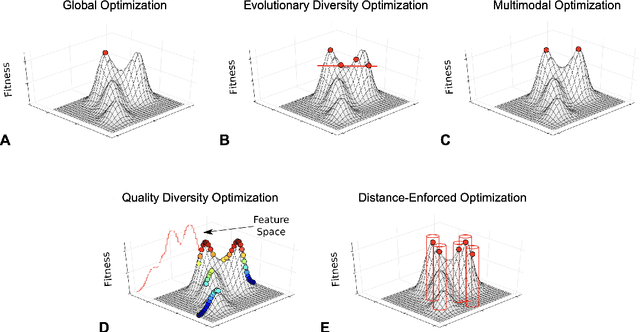
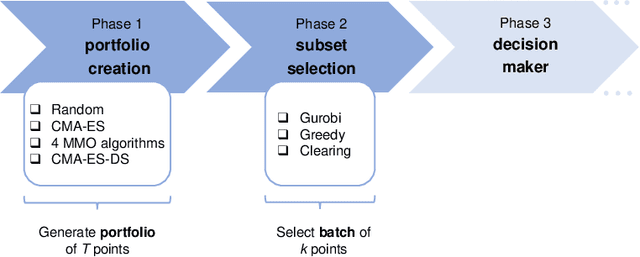
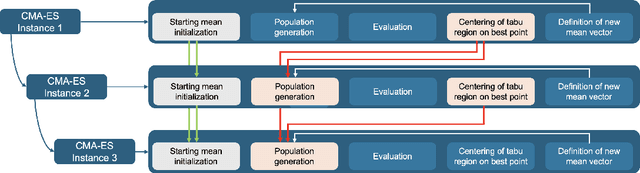
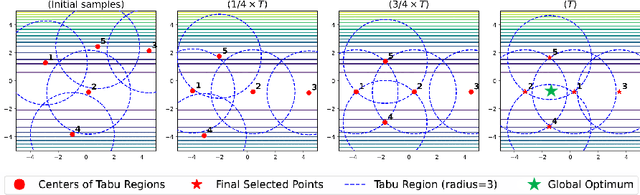
Rather than obtaining a single good solution for a given optimization problem, users often seek alternative design choices, because the best-found solution may perform poorly with respect to additional objectives or constraints that are difficult to capture into the modeling process. Aiming for batches of diverse solutions of high quality is often desirable, as it provides flexibility to accommodate post-hoc user preferences. At the same time, it is crucial that the quality of the best solution found is not compromised. One particular problem setting balancing high quality and diversity is fixing the required minimum distance between solutions while simultaneously obtaining the best possible fitness. Recent work by Santoni et al. [arXiv 2024] revealed that this setting is not well addressed by state-of-the-art algorithms, performing in par or worse than pure random sampling. Driven by this important limitation, we propose a new approach, where parallel runs of the covariance matrix adaptation evolution strategy (CMA-ES) inherit tabu regions in a cascading fashion. We empirically demonstrate that our CMA-ES-Diversity Search (CMA-ES-DS) algorithm generates trajectories that allow to extract high-quality solution batches that respect a given minimum distance requirement, clearly outperforming those obtained from off-the-shelf random sampling, multi-modal optimization algorithms, and standard CMA-ES.

Decision-Theoretic Approaches in Learning-Augmented Algorithms

In this work, we initiate the systemic study of decision-theoretic metrics in the design and analysis of algorithms with machine-learned predictions. We introduce approaches based on both deterministic measures such as distance-based evaluation, that help us quantify how close the algorithm is to an ideal solution, as well as stochastic measures that allow us to balance the trade-off between the algorithm's performance and the risk associated with the imperfect oracle. These approaches help us quantify the algorithmic performance across the entire spectrum of prediction error, unlike several previous works that focus on few, and often extreme values of the error. We apply these techniques to two well-known problems from resource allocation and online decision making, namely contract scheduling and 1-max search.

Overcoming Brittleness in Pareto-Optimal Learning-Augmented Algorithms

The study of online algorithms with machine-learned predictions has gained considerable prominence in recent years. One of the common objectives in the design and analysis of such algorithms is to attain (Pareto) optimal tradeoffs between the consistency of the algorithm, i.e., its performance assuming perfect predictions, and its robustness, i.e., the performance of the algorithm under adversarial predictions. In this work, we demonstrate that this optimization criterion can be extremely brittle, in that the performance of Pareto-optimal algorithms may degrade dramatically even in the presence of imperceptive prediction error. To remedy this drawback, we propose a new framework in which the smoothness in the performance of the algorithm is enforced by means of a user-specified profile. This allows us to regulate the performance of the algorithm as a function of the prediction error, while simultaneously maintaining the analytical notion of consistency/robustness tradeoffs, adapted to the profile setting. We apply this new approach to a well-studied online problem, namely the one-way trading problem. For this problem, we further address another limitation of the state-of-the-art Pareto-optimal algorithms, namely the fact that they are tailored to worst-case, and extremely pessimistic inputs. We propose a new Pareto-optimal algorithm that leverages any deviation from the worst-case input to its benefit, and introduce a new metric that allows us to compare any two Pareto-optimal algorithms via a dominance relation.

Contract Scheduling with Distributional and Multiple Advice

Contract scheduling is a widely studied framework for designing real-time systems with interruptible capabilities. Previous work has showed that a prediction on the interruption time can help improve the performance of contract-based systems, however it has relied on a single prediction that is provided by a deterministic oracle. In this work, we introduce and study more general and realistic learning-augmented settings in which the prediction is in the form of a probability distribution, or it is given as a set of multiple possible interruption times. For both prediction settings, we design and analyze schedules which perform optimally if the prediction is accurate, while simultaneously guaranteeing the best worst-case performance if the prediction is adversarial. We also provide evidence that the resulting system is robust to prediction errors in the distributional setting. Last, we present an experimental evaluation that confirms the theoretical findings, and illustrates the performance improvements that can be attained in practice.

Non-monotone DR-submodular Maximization: Approximation and Regret Guarantees

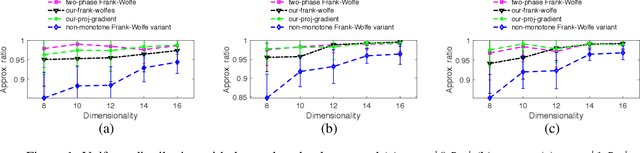
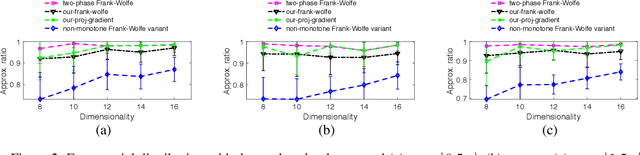
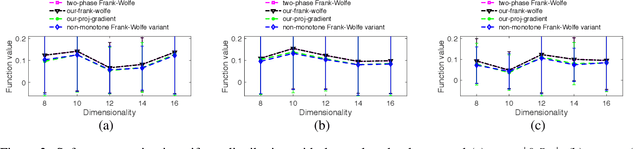
Diminishing-returns (DR) submodular optimization is an important field with many real-world applications in machine learning, economics and communication systems. It captures a subclass of non-convex optimization that provides both practical and theoretical guarantees. In this paper, we study the fundamental problem of maximizing non-monotone DR-submodular functions over down-closed and general convex sets in both offline and online settings. First, we show that for offline maximizing non-monotone DR-submodular functions over a general convex set, the Frank-Wolfe algorithm achieves an approximation guarantee which depends on the convex set. Next, we show that the Stochastic Gradient Ascent algorithm achieves a 1/4-approximation ratio with the regret of $O(1/\sqrt{T})$ for the problem of maximizing non-monotone DR-submodular functions over down-closed convex sets. These are the first approximation guarantees in the corresponding settings. Finally we benchmark these algorithms on problems arising in machine learning domain with the real-world datasets.