Maria Laura Santoni
MECHBench: A Set of Black-Box Optimization Benchmarks originated from Structural Mechanics
Nov 13, 2025Abstract:Benchmarking is essential for developing and evaluating black-box optimization algorithms, providing a structured means to analyze their search behavior. Its effectiveness relies on carefully selected problem sets used for evaluation. To date, most established benchmark suites for black-box optimization consist of abstract or synthetic problems that only partially capture the complexities of real-world engineering applications, thereby severely limiting the insights that can be gained for application-oriented optimization scenarios and reducing their practical impact. To close this gap, we propose a new benchmarking suite that addresses it by presenting a curated set of optimization benchmarks rooted in structural mechanics. The current implemented benchmarks are derived from vehicle crashworthiness scenarios, which inherently require the use of gradient-free algorithms due to the non-smooth, highly non-linear nature of the underlying models. Within this paper, the reader will find descriptions of the physical context of each case, the corresponding optimization problem formulations, and clear guidelines on how to employ the suite.
Cascading CMA-ES Instances for Generating Input-diverse Solution Batches
Feb 19, 2025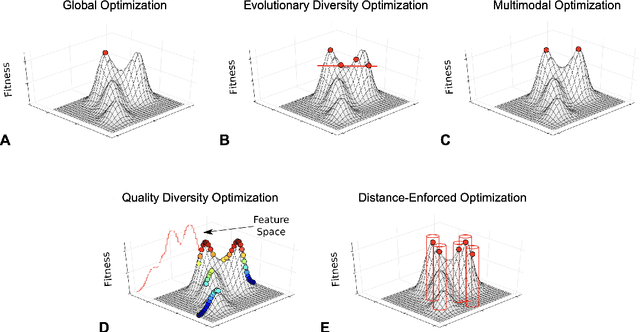
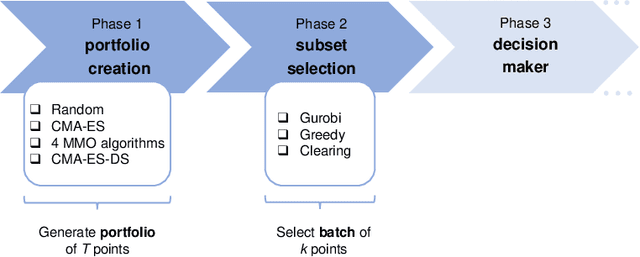
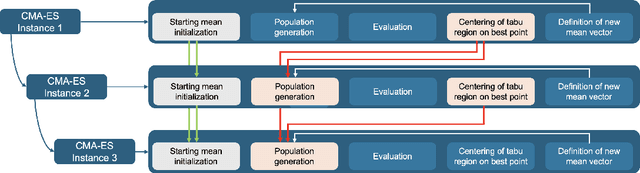
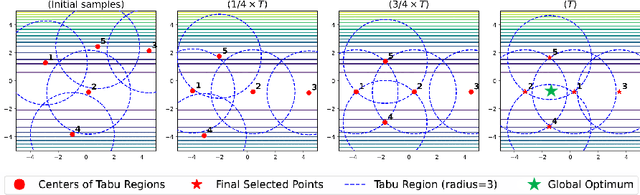
Abstract:Rather than obtaining a single good solution for a given optimization problem, users often seek alternative design choices, because the best-found solution may perform poorly with respect to additional objectives or constraints that are difficult to capture into the modeling process. Aiming for batches of diverse solutions of high quality is often desirable, as it provides flexibility to accommodate post-hoc user preferences. At the same time, it is crucial that the quality of the best solution found is not compromised. One particular problem setting balancing high quality and diversity is fixing the required minimum distance between solutions while simultaneously obtaining the best possible fitness. Recent work by Santoni et al. [arXiv 2024] revealed that this setting is not well addressed by state-of-the-art algorithms, performing in par or worse than pure random sampling. Driven by this important limitation, we propose a new approach, where parallel runs of the covariance matrix adaptation evolution strategy (CMA-ES) inherit tabu regions in a cascading fashion. We empirically demonstrate that our CMA-ES-Diversity Search (CMA-ES-DS) algorithm generates trajectories that allow to extract high-quality solution batches that respect a given minimum distance requirement, clearly outperforming those obtained from off-the-shelf random sampling, multi-modal optimization algorithms, and standard CMA-ES.
Illuminating the Diversity-Fitness Trade-Off in Black-Box Optimization
Aug 29, 2024



Abstract:In real-world applications, users often favor structurally diverse design choices over one high-quality solution. It is hence important to consider more solutions that decision-makers can compare and further explore based on additional criteria. Alongside the existing approaches of evolutionary diversity optimization, quality diversity, and multimodal optimization, this paper presents a fresh perspective on this challenge by considering the problem of identifying a fixed number of solutions with a pairwise distance above a specified threshold while maximizing their average quality. We obtain first insight into these objectives by performing a subset selection on the search trajectories of different well-established search heuristics, whether specifically designed with diversity in mind or not. We emphasize that the main goal of our work is not to present a new algorithm but to look at the problem in a more fundamental and theoretically tractable way by asking the question: What trade-off exists between the minimum distance within batches of solutions and the average quality of their fitness? These insights also provide us with a way of making general claims concerning the properties of optimization problems that shall be useful in turn for benchmarking algorithms of the approaches enumerated above. A possibly surprising outcome of our empirical study is the observation that naive uniform random sampling establishes a very strong baseline for our problem, hardly ever outperformed by the search trajectories of the considered heuristics. We interpret these results as a motivation to develop algorithms tailored to produce diverse solutions of high average quality.
Comparison of High-Dimensional Bayesian Optimization Algorithms on BBOB
Mar 02, 2023



Abstract:Bayesian Optimization (BO) is a class of black-box, surrogate-based heuristics that can efficiently optimize problems that are expensive to evaluate, and hence admit only small evaluation budgets. BO is particularly popular for solving numerical optimization problems in industry, where the evaluation of objective functions often relies on time-consuming simulations or physical experiments. However, many industrial problems depend on a large number of parameters. This poses a challenge for BO algorithms, whose performance is often reported to suffer when the dimension grows beyond 15 variables. Although many new algorithms have been proposed to address this problem, it is not well understood which one is the best for which optimization scenario. In this work, we compare five state-of-the-art high-dimensional BO algorithms, with vanilla BO and CMA-ES on the 24 BBOB functions of the COCO environment at increasing dimensionality, ranging from 10 to 60 variables. Our results confirm the superiority of BO over CMA-ES for limited evaluation budgets and suggest that the most promising approach to improve BO is the use of trust regions. However, we also observe significant performance differences for different function landscapes and budget exploitation phases, indicating improvement potential, e.g., through hybridization of algorithmic components.
PI is back! Switching Acquisition Functions in Bayesian Optimization
Nov 02, 2022



Abstract:Bayesian Optimization (BO) is a powerful, sample-efficient technique to optimize expensive-to-evaluate functions. Each of the BO components, such as the surrogate model, the acquisition function (AF), or the initial design, is subject to a wide range of design choices. Selecting the right components for a given optimization task is a challenging task, which can have significant impact on the quality of the obtained results. In this work, we initiate the analysis of which AF to favor for which optimization scenarios. To this end, we benchmark SMAC3 using Expected Improvement (EI) and Probability of Improvement (PI) as acquisition functions on the 24 BBOB functions of the COCO environment. We compare their results with those of schedules switching between AFs. One schedule aims to use EI's explorative behavior in the early optimization steps, and then switches to PI for a better exploitation in the final steps. We also compare this to a random schedule and round-robin selection of EI and PI. We observe that dynamic schedules oftentimes outperform any single static one. Our results suggest that a schedule that allocates the first 25 % of the optimization budget to EI and the last 75 % to PI is a reliable default. However, we also observe considerable performance differences for the 24 functions, suggesting that a per-instance allocation, possibly learned on the fly, could offer significant improvement over the state-of-the-art BO designs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge