TinyverseGP: Towards a Modular Cross-domain Benchmarking Framework for Genetic Programming

Over the years, genetic programming (GP) has evolved, with many proposed variations, especially in how they represent a solution. Being essentially a program synthesis algorithm, it is capable of tackling multiple problem domains. Current benchmarking initiatives are fragmented, as the different representations are not compared with each other and their performance is not measured across the different domains. In this work, we propose a unified framework, dubbed TinyverseGP (inspired by tinyGP), which provides support to multiple representations and problem domains, including symbolic regression, logic synthesis and policy search.

PS-AAS: Portfolio Selection for Automated Algorithm Selection in Black-Box Optimization

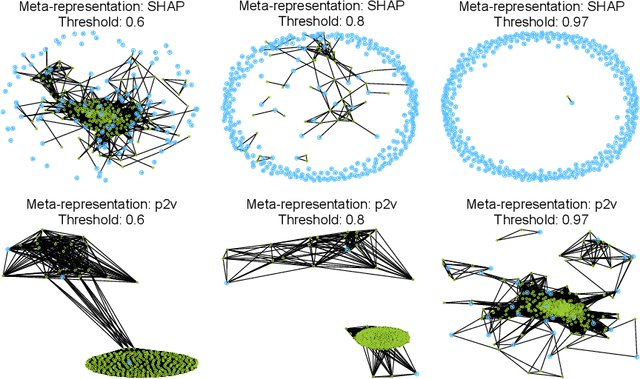
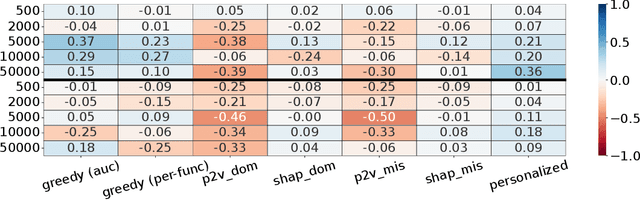
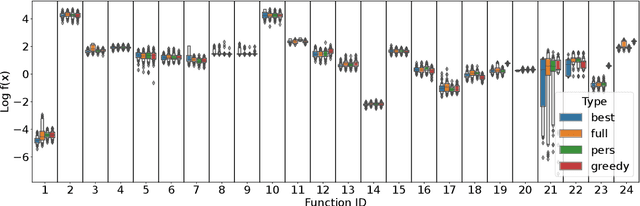
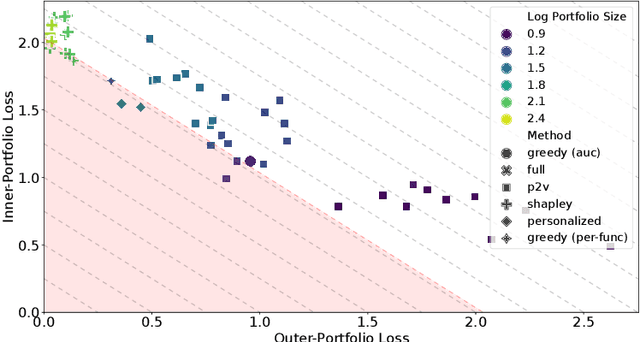
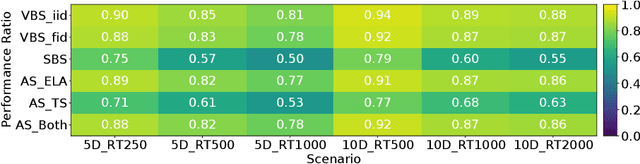
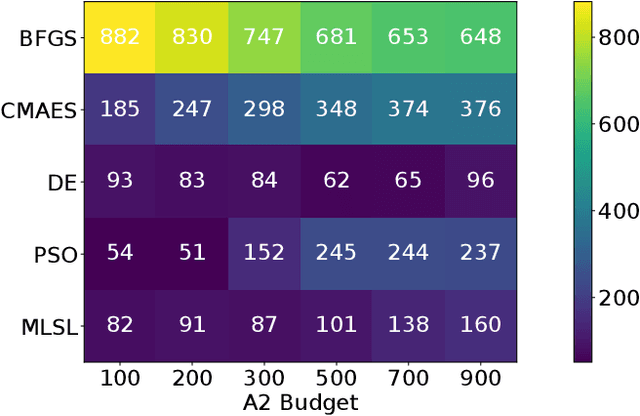
The performance of automated algorithm selection (AAS) strongly depends on the portfolio of algorithms to choose from. Selecting the portfolio is a non-trivial task that requires balancing the trade-off between the higher flexibility of large portfolios with the increased complexity of the AAS task. In practice, probably the most common way to choose the algorithms for the portfolio is a greedy selection of the algorithms that perform well in some reference tasks of interest. We set out in this work to investigate alternative, data-driven portfolio selection techniques. Our proposed method creates algorithm behavior meta-representations, constructs a graph from a set of algorithms based on their meta-representation similarity, and applies a graph algorithm to select a final portfolio of diverse, representative, and non-redundant algorithms. We evaluate two distinct meta-representation techniques (SHAP and performance2vec) for selecting complementary portfolios from a total of 324 different variants of CMA-ES for the task of optimizing the BBOB single-objective problems in dimensionalities 5 and 30 with different cut-off budgets. We test two types of portfolios: one related to overall algorithm behavior and the `personalized' one (related to algorithm behavior per each problem separately). We observe that the approach built on the performance2vec-based representations favors small portfolios with negligible error in the AAS task relative to the virtual best solver from the selected portfolio, whereas the portfolios built from the SHAP-based representations gain from higher flexibility at the cost of decreased performance of the AAS. Across most considered scenarios, personalized portfolios yield comparable or slightly better performance than the classical greedy approach. They outperform the full portfolio in all scenarios.

Self-Adjusting Weighted Expected Improvement for Bayesian Optimization

Bayesian Optimization (BO) is a class of surrogate-based, sample-efficient algorithms for optimizing black-box problems with small evaluation budgets. The BO pipeline itself is highly configurable with many different design choices regarding the initial design, surrogate model, and acquisition function (AF). Unfortunately, our understanding of how to select suitable components for a problem at hand is very limited. In this work, we focus on the definition of the AF, whose main purpose is to balance the trade-off between exploring regions with high uncertainty and those with high promise for good solutions. We propose Self-Adjusting Weighted Expected Improvement (SAWEI), where we let the exploration-exploitation trade-off self-adjust in a data-driven manner, based on a convergence criterion for BO. On the noise-free black-box BBOB functions of the COCO benchmarking platform, our method exhibits a favorable any-time performance compared to handcrafted baselines and serves as a robust default choice for any problem structure. The suitability of our method also transfers to HPOBench. With SAWEI, we are a step closer to on-the-fly, data-driven, and robust BO designs that automatically adjust their sampling behavior to the problem at hand.

Comparing Algorithm Selection Approaches on Black-Box Optimization Problems

Performance complementarity of solvers available to tackle black-box optimization problems gives rise to the important task of algorithm selection (AS). Automated AS approaches can help replace tedious and labor-intensive manual selection, and have already shown promising performance in various optimization domains. Automated AS relies on machine learning (ML) techniques to recommend the best algorithm given the information about the problem instance. Unfortunately, there are no clear guidelines for choosing the most appropriate one from a variety of ML techniques. Tree-based models such as Random Forest or XGBoost have consistently demonstrated outstanding performance for automated AS. Transformers and other tabular deep learning models have also been increasingly applied in this context. We investigate in this work the impact of the choice of the ML technique on AS performance. We compare four ML models on the task of predicting the best solver for the BBOB problems for 7 different runtime budgets in 2 dimensions. While our results confirm that a per-instance AS has indeed impressive potential, we also show that the particular choice of the ML technique is of much minor importance.

Towards Automated Design of Bayesian Optimization via Exploratory Landscape Analysis

Bayesian optimization (BO) algorithms form a class of surrogate-based heuristics, aimed at efficiently computing high-quality solutions for numerical black-box optimization problems. The BO pipeline is highly modular, with different design choices for the initial sampling strategy, the surrogate model, the acquisition function (AF), the solver used to optimize the AF, etc. We demonstrate in this work that a dynamic selection of the AF can benefit the BO design. More precisely, we show that already a na\"ive random forest regression model, built on top of exploratory landscape analysis features that are computed from the initial design points, suffices to recommend AFs that outperform any static choice, when considering performance over the classic BBOB benchmark suite for derivative-free numerical optimization methods on the COCO platform. Our work hence paves a way towards AutoML-assisted, on-the-fly BO designs that adjust their behavior on a run-by-run basis.

PI is back! Switching Acquisition Functions in Bayesian Optimization

Bayesian Optimization (BO) is a powerful, sample-efficient technique to optimize expensive-to-evaluate functions. Each of the BO components, such as the surrogate model, the acquisition function (AF), or the initial design, is subject to a wide range of design choices. Selecting the right components for a given optimization task is a challenging task, which can have significant impact on the quality of the obtained results. In this work, we initiate the analysis of which AF to favor for which optimization scenarios. To this end, we benchmark SMAC3 using Expected Improvement (EI) and Probability of Improvement (PI) as acquisition functions on the 24 BBOB functions of the COCO environment. We compare their results with those of schedules switching between AFs. One schedule aims to use EI's explorative behavior in the early optimization steps, and then switches to PI for a better exploitation in the final steps. We also compare this to a random schedule and round-robin selection of EI and PI. We observe that dynamic schedules oftentimes outperform any single static one. Our results suggest that a schedule that allocates the first 25 % of the optimization budget to EI and the last 75 % to PI is a reliable default. However, we also observe considerable performance differences for the 24 functions, suggesting that a per-instance allocation, possibly learned on the fly, could offer significant improvement over the state-of-the-art BO designs.

Per-run Algorithm Selection with Warm-starting using Trajectory-based Features

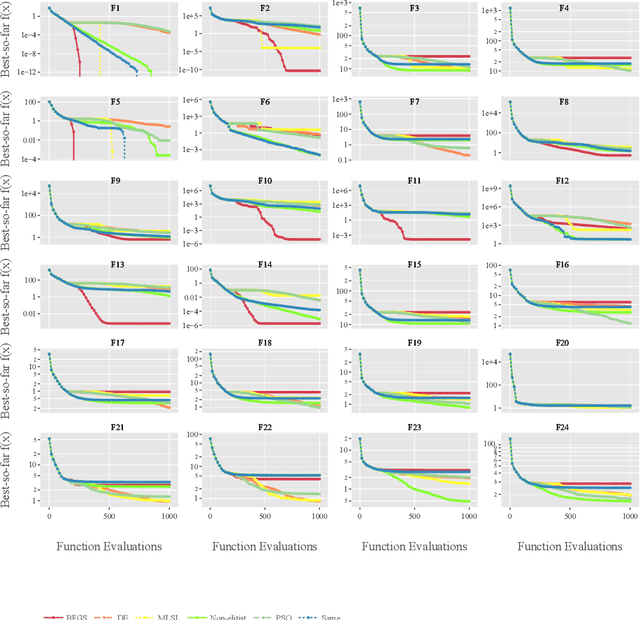
Per-instance algorithm selection seeks to recommend, for a given problem instance and a given performance criterion, one or several suitable algorithms that are expected to perform well for the particular setting. The selection is classically done offline, using openly available information about the problem instance or features that are extracted from the instance during a dedicated feature extraction step. This ignores valuable information that the algorithms accumulate during the optimization process. In this work, we propose an alternative, online algorithm selection scheme which we coin per-run algorithm selection. In our approach, we start the optimization with a default algorithm, and, after a certain number of iterations, extract instance features from the observed trajectory of this initial optimizer to determine whether to switch to another optimizer. We test this approach using the CMA-ES as the default solver, and a portfolio of six different optimizers as potential algorithms to switch to. In contrast to other recent work on online per-run algorithm selection, we warm-start the second optimizer using information accumulated during the first optimization phase. We show that our approach outperforms static per-instance algorithm selection. We also compare two different feature extraction principles, based on exploratory landscape analysis and time series analysis of the internal state variables of the CMA-ES, respectively. We show that a combination of both feature sets provides the most accurate recommendations for our test cases, taken from the BBOB function suite from the COCO platform and the YABBOB suite from the Nevergrad platform.

Trajectory-based Algorithm Selection with Warm-starting

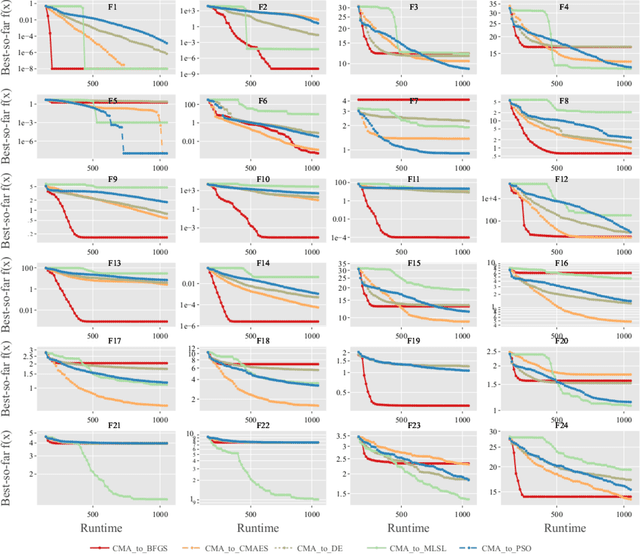
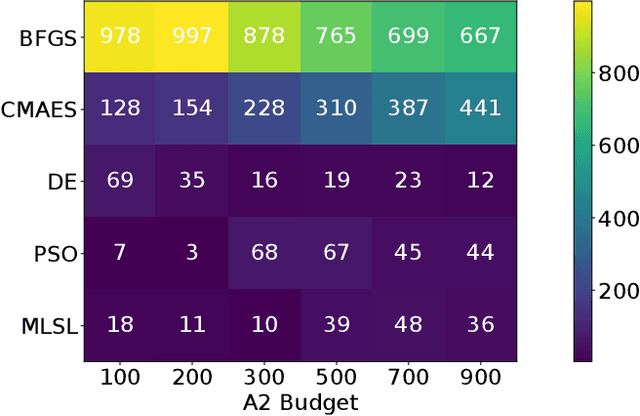
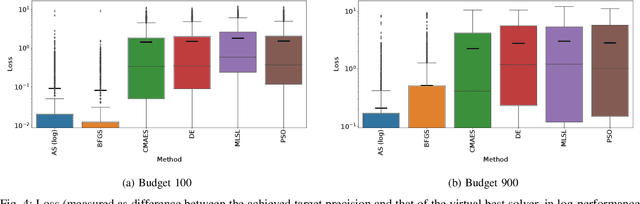
Landscape-aware algorithm selection approaches have so far mostly been relying on landscape feature extraction as a preprocessing step, independent of the execution of optimization algorithms in the portfolio. This introduces a significant overhead in computational cost for many practical applications, as features are extracted and computed via sampling and evaluating the problem instance at hand, similarly to what the optimization algorithm would perform anyway within its search trajectory. As suggested in Jankovic et al. (EvoAPPs 2021), trajectory-based algorithm selection circumvents the problem of costly feature extraction by computing landscape features from points that a solver sampled and evaluated during the optimization process. Features computed in this manner are used to train algorithm performance regression models, upon which a per-run algorithm selector is then built. In this work, we apply the trajectory-based approach onto a portfolio of five algorithms. We study the quality and accuracy of performance regression and algorithm selection models in the scenario of predicting different algorithm performances after a fixed budget of function evaluations. We rely on landscape features of the problem instance computed using one portion of the aforementioned budget of the same function evaluations. Moreover, we consider the possibility of switching between the solvers once, which requires them to be warm-started, i.e. when we switch, the second solver continues the optimization process already being initialized appropriately by making use of the information collected by the first solver. In this new context, we show promising performance of the trajectory-based per-run algorithm selection with warm-starting.

Personalizing Performance Regression Models to Black-Box Optimization Problems

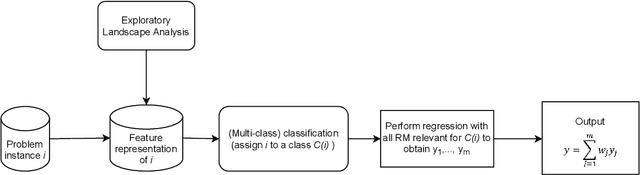
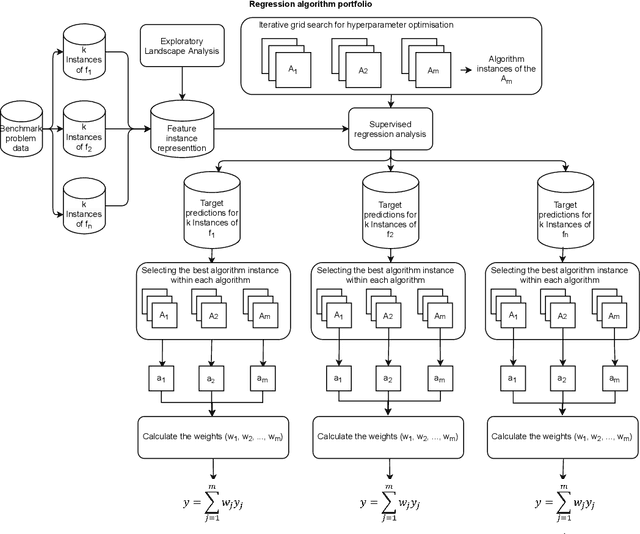
Accurately predicting the performance of different optimization algorithms for previously unseen problem instances is crucial for high-performing algorithm selection and configuration techniques. In the context of numerical optimization, supervised regression approaches built on top of exploratory landscape analysis are becoming very popular. From the point of view of Machine Learning (ML), however, the approaches are often rather naive, using default regression or classification techniques without proper investigation of the suitability of the ML tools. With this work, we bring to the attention of our community the possibility to personalize regression models to specific types of optimization problems. Instead of aiming for a single model that works well across a whole set of possibly diverse problems, our personalized regression approach acknowledges that different models may suite different types of problems. Going one step further, we also investigate the impact of selecting not a single regression model per problem, but personalized ensembles. We test our approach on predicting the performance of numerical optimization heuristics on the BBOB benchmark collection.

The Impact of Hyper-Parameter Tuning for Landscape-Aware Performance Regression and Algorithm Selection

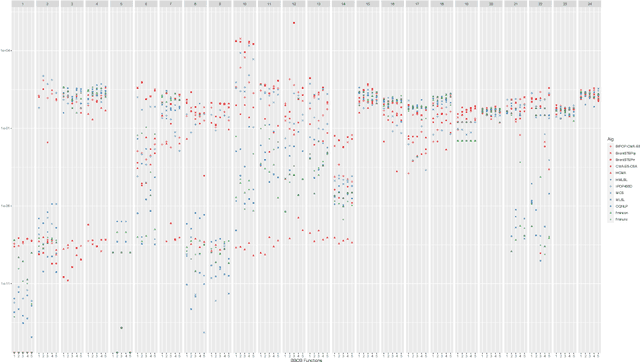
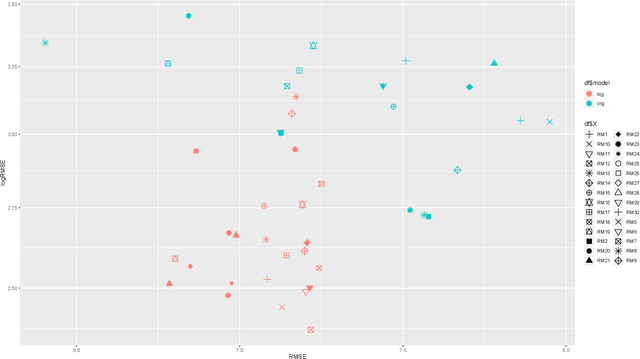
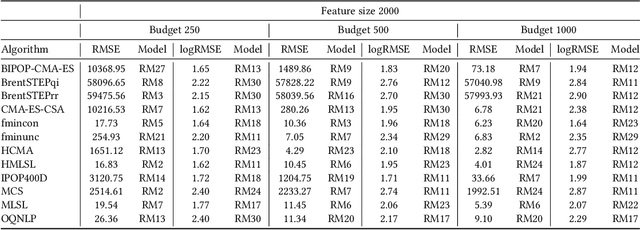
Automated algorithm selection and configuration methods that build on exploratory landscape analysis (ELA) are becoming very popular in Evolutionary Computation. However, despite a significantly growing number of applications, the underlying machine learning models are often chosen in an ad-hoc manner. We show in this work that three classical regression methods are able to achieve meaningful results for ELA-based algorithm selection. For those three models -- random forests, decision trees, and bagging decision trees -- the quality of the regression models is highly impacted by the chosen hyper-parameters. This has significant effects also on the quality of the algorithm selectors that are built on top of these regressions. By comparing a total number of 30 different models, each coupled with 2 complementary regression strategies, we derive guidelines for the tuning of the regression models and provide general recommendations for a more systematic use of classical machine learning models in landscape-aware algorithm selection. We point out that a choice of the machine learning model merits to be carefully undertaken and further investigated.