Personalizing Performance Regression Models to Black-Box Optimization Problems

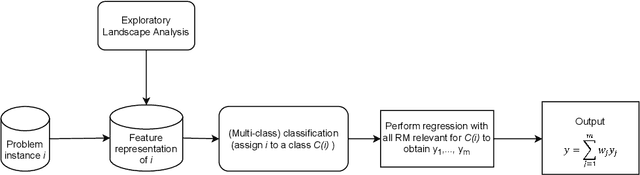
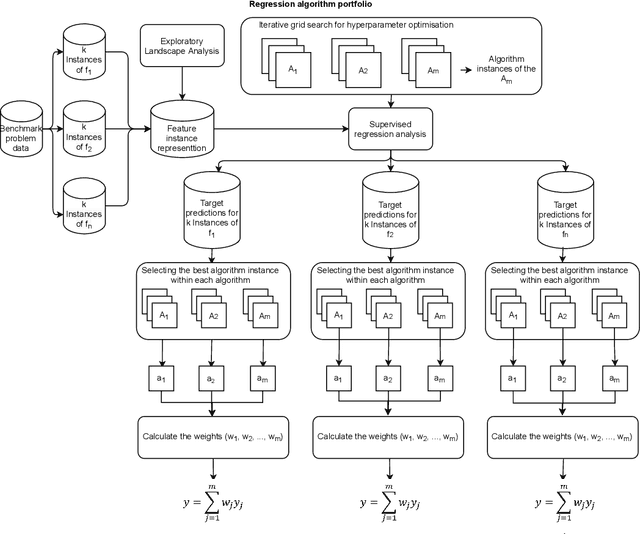
Accurately predicting the performance of different optimization algorithms for previously unseen problem instances is crucial for high-performing algorithm selection and configuration techniques. In the context of numerical optimization, supervised regression approaches built on top of exploratory landscape analysis are becoming very popular. From the point of view of Machine Learning (ML), however, the approaches are often rather naive, using default regression or classification techniques without proper investigation of the suitability of the ML tools. With this work, we bring to the attention of our community the possibility to personalize regression models to specific types of optimization problems. Instead of aiming for a single model that works well across a whole set of possibly diverse problems, our personalized regression approach acknowledges that different models may suite different types of problems. Going one step further, we also investigate the impact of selecting not a single regression model per problem, but personalized ensembles. We test our approach on predicting the performance of numerical optimization heuristics on the BBOB benchmark collection.

The Impact of Hyper-Parameter Tuning for Landscape-Aware Performance Regression and Algorithm Selection

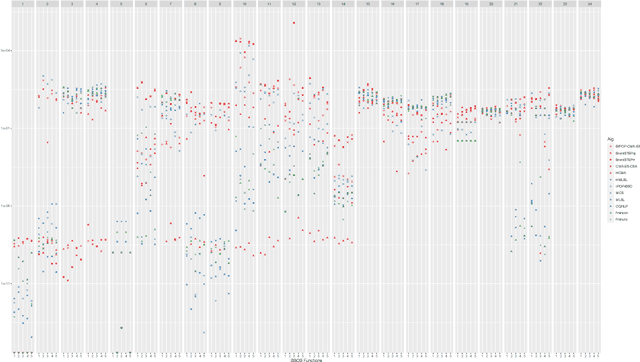
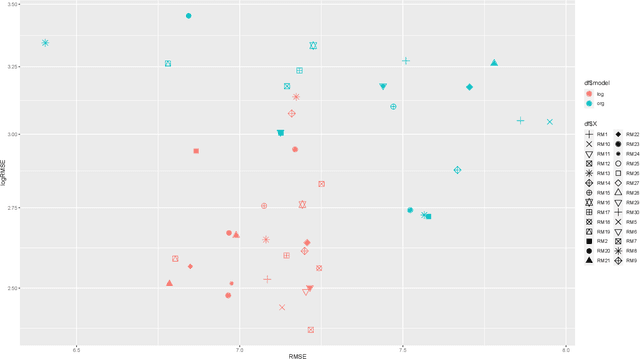
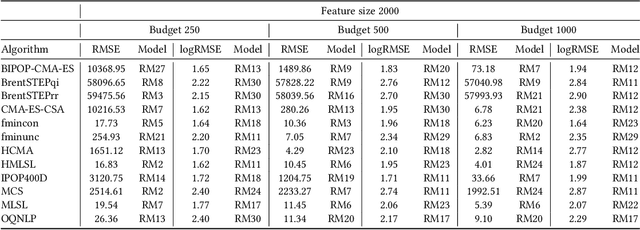
Automated algorithm selection and configuration methods that build on exploratory landscape analysis (ELA) are becoming very popular in Evolutionary Computation. However, despite a significantly growing number of applications, the underlying machine learning models are often chosen in an ad-hoc manner. We show in this work that three classical regression methods are able to achieve meaningful results for ELA-based algorithm selection. For those three models -- random forests, decision trees, and bagging decision trees -- the quality of the regression models is highly impacted by the chosen hyper-parameters. This has significant effects also on the quality of the algorithm selectors that are built on top of these regressions. By comparing a total number of 30 different models, each coupled with 2 complementary regression strategies, we derive guidelines for the tuning of the regression models and provide general recommendations for a more systematic use of classical machine learning models in landscape-aware algorithm selection. We point out that a choice of the machine learning model merits to be carefully undertaken and further investigated.

Linear Matrix Factorization Embeddings for Single-objective Optimization Landscapes

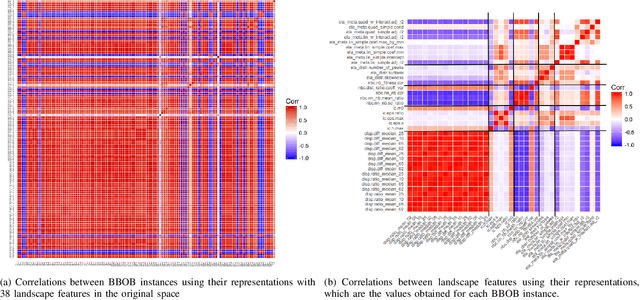
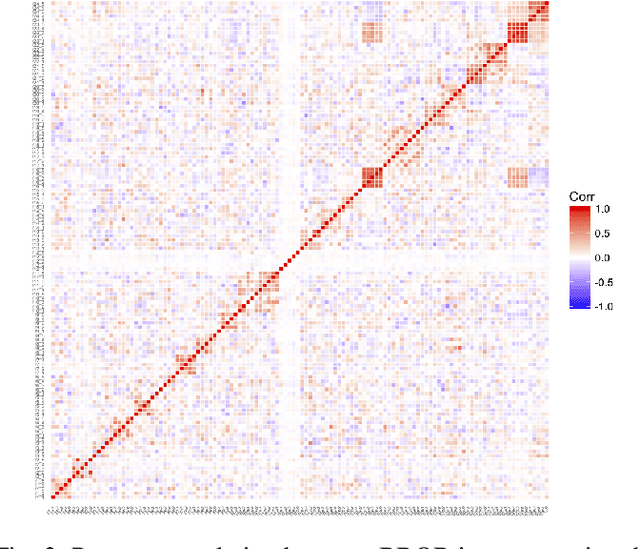
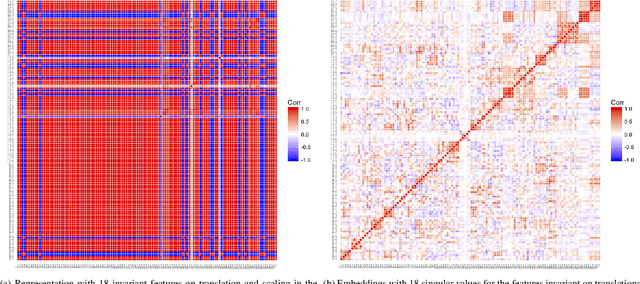
Automated per-instance algorithm selection and configuration have shown promising performances for a number of classic optimization problems, including satisfiability, AI planning, and TSP. The techniques often rely on a set of features that measure some characteristics of the problem instance at hand. In the context of black-box optimization, these features have to be derived from a set of $(x,f(x))$ samples. A number of different features have been proposed in the literature, measuring, for example, the modality, the separability, or the ruggedness of the instance at hand. Several of the commonly used features, however, are highly correlated. While state-of-the-art machine learning techniques can routinely filter such correlations, they hinder explainability of the derived algorithm design techniques. We therefore propose in this work to pre-process the measured (raw) landscape features through representation learning. More precisely, we show that a linear dimensionality reduction via matrix factorization significantly contributes towards a better detection of correlation between different problem instances -- a key prerequisite for successful automated algorithm design.