PS-AAS: Portfolio Selection for Automated Algorithm Selection in Black-Box Optimization

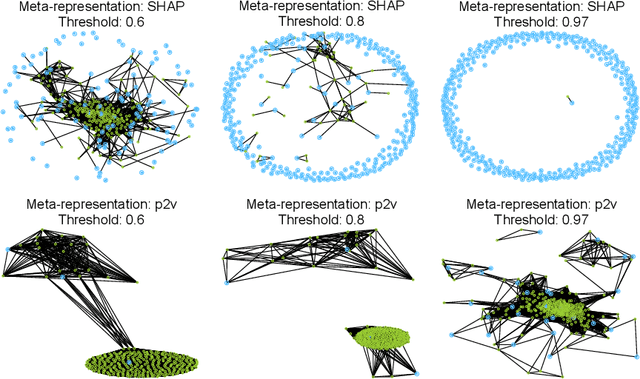
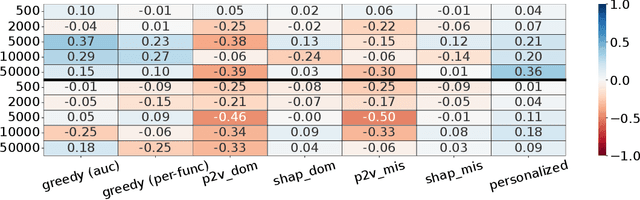
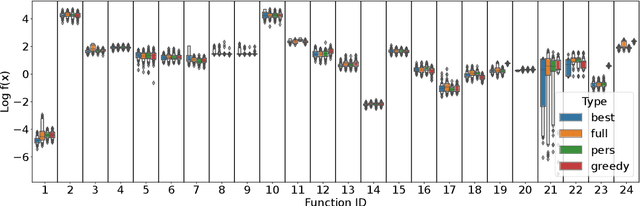
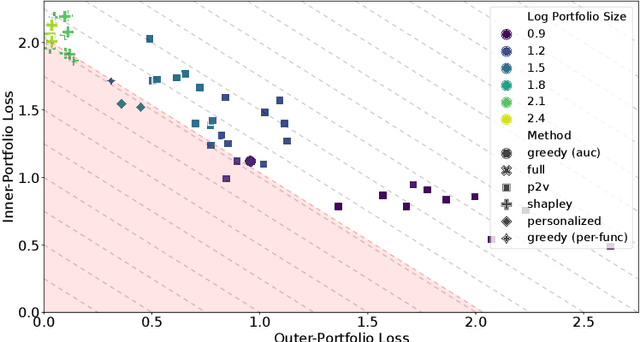
The performance of automated algorithm selection (AAS) strongly depends on the portfolio of algorithms to choose from. Selecting the portfolio is a non-trivial task that requires balancing the trade-off between the higher flexibility of large portfolios with the increased complexity of the AAS task. In practice, probably the most common way to choose the algorithms for the portfolio is a greedy selection of the algorithms that perform well in some reference tasks of interest. We set out in this work to investigate alternative, data-driven portfolio selection techniques. Our proposed method creates algorithm behavior meta-representations, constructs a graph from a set of algorithms based on their meta-representation similarity, and applies a graph algorithm to select a final portfolio of diverse, representative, and non-redundant algorithms. We evaluate two distinct meta-representation techniques (SHAP and performance2vec) for selecting complementary portfolios from a total of 324 different variants of CMA-ES for the task of optimizing the BBOB single-objective problems in dimensionalities 5 and 30 with different cut-off budgets. We test two types of portfolios: one related to overall algorithm behavior and the `personalized' one (related to algorithm behavior per each problem separately). We observe that the approach built on the performance2vec-based representations favors small portfolios with negligible error in the AAS task relative to the virtual best solver from the selected portfolio, whereas the portfolios built from the SHAP-based representations gain from higher flexibility at the cost of decreased performance of the AAS. Across most considered scenarios, personalized portfolios yield comparable or slightly better performance than the classical greedy approach. They outperform the full portfolio in all scenarios.

Linear Matrix Factorization Embeddings for Single-objective Optimization Landscapes

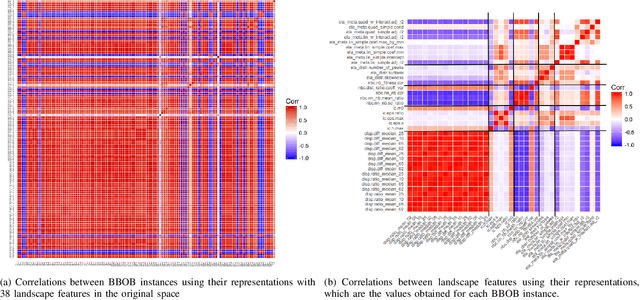
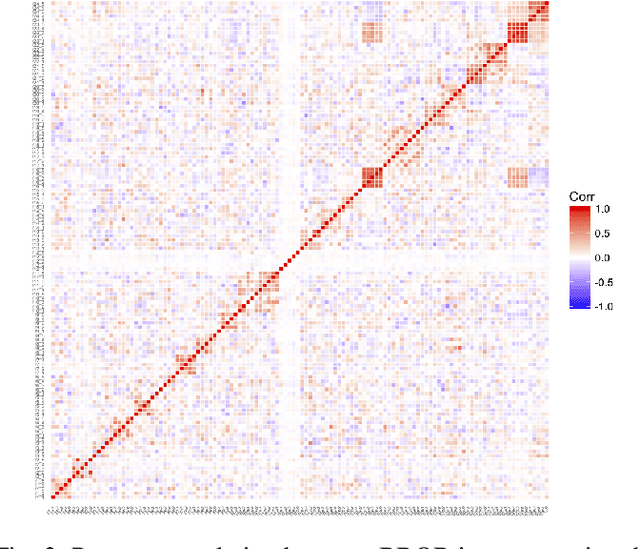
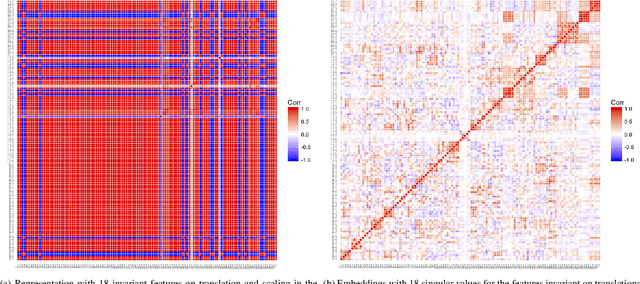
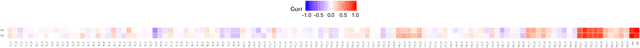
Automated per-instance algorithm selection and configuration have shown promising performances for a number of classic optimization problems, including satisfiability, AI planning, and TSP. The techniques often rely on a set of features that measure some characteristics of the problem instance at hand. In the context of black-box optimization, these features have to be derived from a set of $(x,f(x))$ samples. A number of different features have been proposed in the literature, measuring, for example, the modality, the separability, or the ruggedness of the instance at hand. Several of the commonly used features, however, are highly correlated. While state-of-the-art machine learning techniques can routinely filter such correlations, they hinder explainability of the derived algorithm design techniques. We therefore propose in this work to pre-process the measured (raw) landscape features through representation learning. More precisely, we show that a linear dimensionality reduction via matrix factorization significantly contributes towards a better detection of correlation between different problem instances -- a key prerequisite for successful automated algorithm design.