Overcoming Brittleness in Pareto-Optimal Learning-Augmented Algorithms

The study of online algorithms with machine-learned predictions has gained considerable prominence in recent years. One of the common objectives in the design and analysis of such algorithms is to attain (Pareto) optimal tradeoffs between the consistency of the algorithm, i.e., its performance assuming perfect predictions, and its robustness, i.e., the performance of the algorithm under adversarial predictions. In this work, we demonstrate that this optimization criterion can be extremely brittle, in that the performance of Pareto-optimal algorithms may degrade dramatically even in the presence of imperceptive prediction error. To remedy this drawback, we propose a new framework in which the smoothness in the performance of the algorithm is enforced by means of a user-specified profile. This allows us to regulate the performance of the algorithm as a function of the prediction error, while simultaneously maintaining the analytical notion of consistency/robustness tradeoffs, adapted to the profile setting. We apply this new approach to a well-studied online problem, namely the one-way trading problem. For this problem, we further address another limitation of the state-of-the-art Pareto-optimal algorithms, namely the fact that they are tailored to worst-case, and extremely pessimistic inputs. We propose a new Pareto-optimal algorithm that leverages any deviation from the worst-case input to its benefit, and introduce a new metric that allows us to compare any two Pareto-optimal algorithms via a dominance relation.

Contract Scheduling with Distributional and Multiple Advice

Contract scheduling is a widely studied framework for designing real-time systems with interruptible capabilities. Previous work has showed that a prediction on the interruption time can help improve the performance of contract-based systems, however it has relied on a single prediction that is provided by a deterministic oracle. In this work, we introduce and study more general and realistic learning-augmented settings in which the prediction is in the form of a probability distribution, or it is given as a set of multiple possible interruption times. For both prediction settings, we design and analyze schedules which perform optimally if the prediction is accurate, while simultaneously guaranteeing the best worst-case performance if the prediction is adversarial. We also provide evidence that the resulting system is robust to prediction errors in the distributional setting. Last, we present an experimental evaluation that confirms the theoretical findings, and illustrates the performance improvements that can be attained in practice.

Online Search With Best-Price and Query-Based Predictions

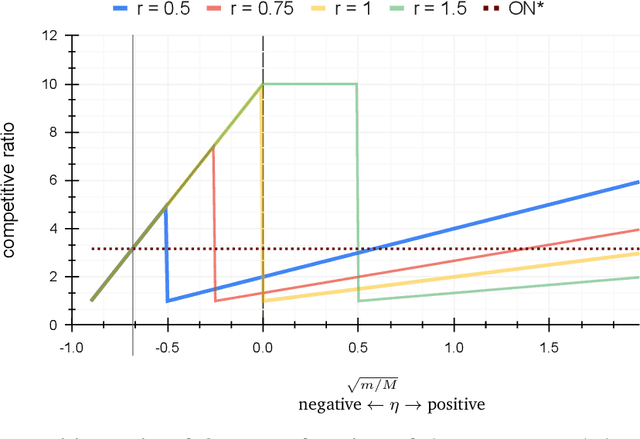
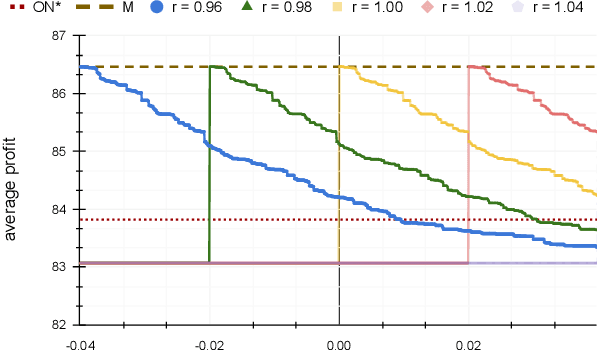
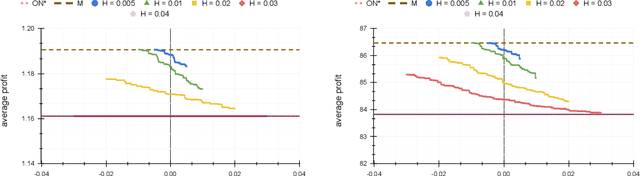
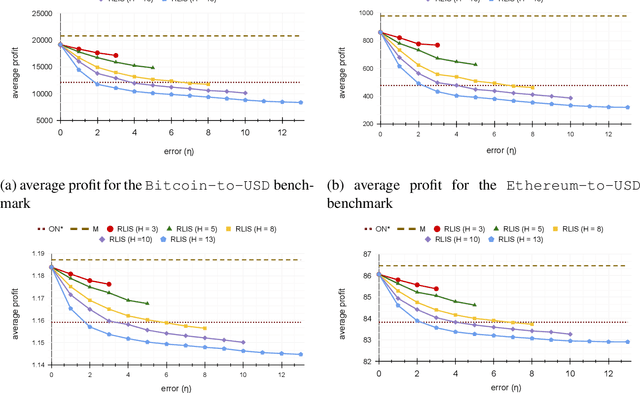
In the online (time-series) search problem, a player is presented with a sequence of prices which are revealed in an online manner. In the standard definition of the problem, for each revealed price, the player must decide irrevocably whether to accept or reject it, without knowledge of future prices (other than an upper and a lower bound on their extreme values), and the objective is to minimize the competitive ratio, namely the worst-case ratio between the maximum price in the sequence and the one selected by the player. The problem formulates several applications of decision-making in the face of uncertainty on the revealed samples. Previous work on this problem has largely assumed extreme scenarios in which either the player has almost no information about the input, or the player is provided with some powerful, and error-free advice. In this work, we study learning-augmented algorithms, in which there is a potentially erroneous prediction concerning the input. Specifically, we consider two different settings: the setting in which the prediction is related to the maximum price in the sequence, as well as the setting in which the prediction is obtained as a response to a number of binary queries. For both settings, we provide tight, or near-tight upper and lower bounds on the worst-case performance of search algorithms as a function of the prediction error. We also provide experimental results on data obtained from stock exchange markets that confirm the theoretical analysis, and explain how our techniques can be applicable to other learning-augmented applications.

Online Bin Packing with Predictions

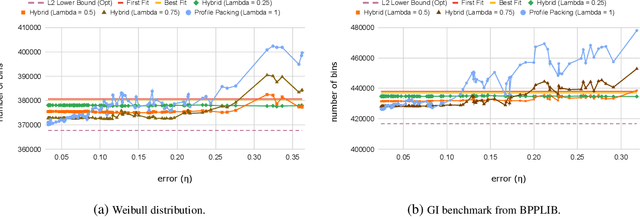
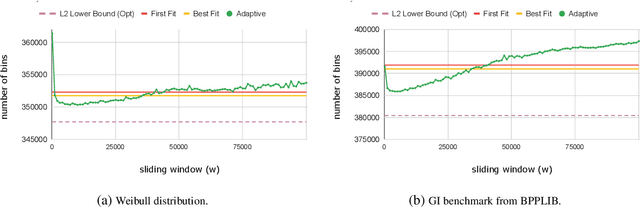
Bin packing is a classic optimization problem with a wide range of applications from load balancing in networks to supply chain management. In this work we study the online variant of the problem, in which a sequence of items of various sizes must be placed into a minimum number of bins of uniform capacity. The online algorithm is enhanced with a (potentially erroneous) prediction concerning the frequency of item sizes in the sequence. We design and analyze online algorithms with efficient tradeoffs between their consistency (i.e., the competitive ratio assuming no prediction error) and their robustness (i.e., the competitive ratio under adversarial error), and whose performance degrades gently as a function of the error. Previous work on this problem has only addressed the extreme cases with respect to the prediction error, and has relied on overly powerful and error-free prediction oracles.

Contract Scheduling With Predictions

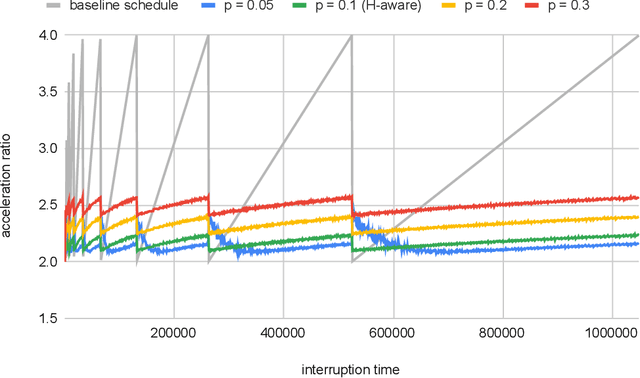
Contract scheduling is a general technique that allows to design a system with interruptible capabilities, given an algorithm that is not necessarily interruptible. Previous work on this topic has largely assumed that the interruption is a worst-case deadline that is unknown to the scheduler. In this work, we study the setting in which there is a potentially erroneous prediction concerning the interruption. Specifically, we consider the setting in which the prediction describes the time that the interruption occurs, as well as the setting in which the prediction is obtained as a response to a single or multiple binary queries. For both settings, we investigate tradeoffs between the robustness (i.e., the worst-case performance assuming adversarial prediction) and the consistency (i.e, the performance assuming that the prediction is error-free), both from the side of positive and negative results.

Interruptible Algorithms for Multiproblem Solving

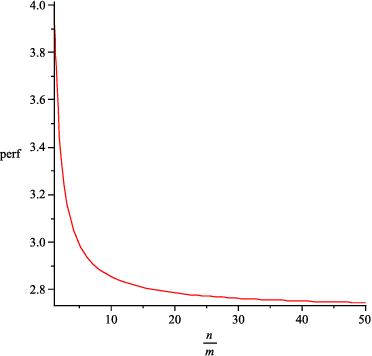
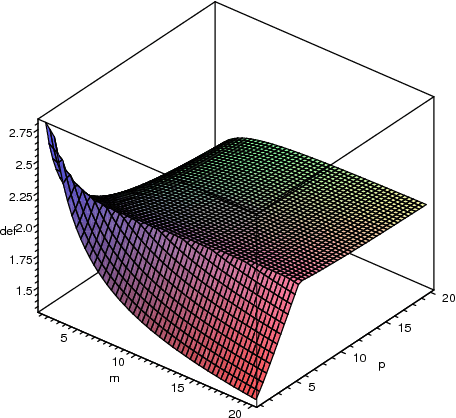
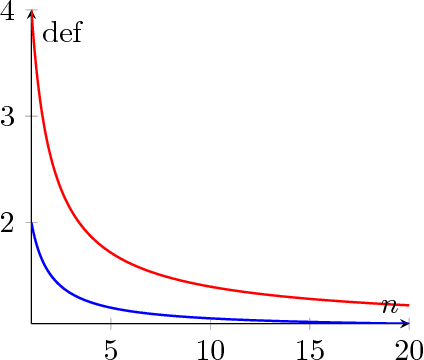
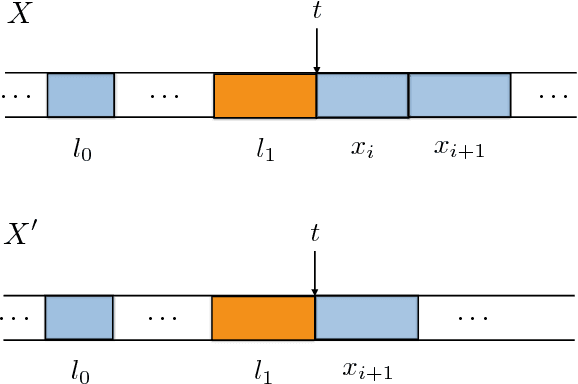
In this paper we address the problem of designing an interruptible system in a setting in which $n$ problem instances, all equally important, must be solved concurrently. The system involves scheduling executions of contract algorithms (which offer a trade-off between allowable computation time and quality of the solution) in m identical parallel processors. When an interruption occurs, the system must report a solution to each of the $n$ problem instances. The quality of this output is then compared to the best-possible algorithm that has foreknowledge of the interruption time and must, likewise, produce solutions to all $n$ problem instances. This extends the well-studied setting in which only one problem instance is queried at interruption time. In this work we first introduce new measures for evaluating the performance of interruptible systems in this setting. In particular, we propose the deficiency of a schedule as a performance measure that meets the requirements of the problem at hand. We then present a schedule whose performance we prove that is within a small factor from optimal in the general, multiprocessor setting. We also show several lower bounds on the deficiency of schedules on a single processor. More precisely, we prove a general lower bound of (n+1)/n, an improved lower bound for the two-problem setting (n=2), and a tight lower bound for the class of round-robin schedules. Our techniques can also yield a simpler, alternative proof of the main result of [Bernstein et al, IJCAI 2003] concerning the performance of cyclic schedules in multiprocessor environments.

Further Connections Between Contract-Scheduling and Ray-Searching Problems

This paper addresses two classes of different, yet interrelated optimization problems. The first class of problems involves a robot that must locate a hidden target in an environment that consists of a set of concurrent rays. The second class pertains to the design of interruptible algorithms by means of a schedule of contract algorithms. We study several variants of these families of problems, such as searching and scheduling with probabilistic considerations, redundancy and fault-tolerance issues, randomized strategies, and trade-offs between performance and preemptions. For many of these problems we present the first known results that apply to multi-ray and multi-problem domains. Our objective is to demonstrate that several well-motivated settings can be addressed using the same underlying approach.