Shahin Kamali
Robust Learning-Augmented Dictionaries
Feb 15, 2024Abstract:We present the first learning-augmented data structure for implementing dictionaries with optimal consistency and robustness. Our data structure, named RobustSL, is a skip list augmented by predictions of access frequencies of elements in a data sequence. With proper predictions, RobustSL has optimal consistency (achieves static optimality). At the same time, it maintains a logarithmic running time for each operation, ensuring optimal robustness, even if predictions are generated adversarially. Therefore, RobustSL has all the advantages of the recent learning-augmented data structures of Lin, Luo, and Woodruff (ICML 2022) and Cao et al. (arXiv 2023), while providing robustness guarantees that are absent in the previous work. Numerical experiments show that RobustSL outperforms alternative data structures using both synthetic and real datasets.
Time Fairness in Online Knapsack Problems
May 22, 2023



Abstract:The online knapsack problem is a classic problem in the field of online algorithms. Its canonical version asks how to pack items of different values and weights arriving online into a capacity-limited knapsack so as to maximize the total value of the admitted items. Although optimal competitive algorithms are known for this problem, they may be fundamentally unfair, i.e., individual items may be treated inequitably in different ways. Inspired by recent attention to fairness in online settings, we develop a natural and practically-relevant notion of time fairness for the online knapsack problem, and show that the existing optimal algorithms perform poorly under this metric. We propose a parameterized deterministic algorithm where the parameter precisely captures the Pareto-optimal trade-off between fairness and competitiveness. We show that randomization is theoretically powerful enough to be simultaneously competitive and fair; however, it does not work well in practice, using trace-driven experiments. To further improve the trade-off between fairness and competitiveness, we develop a fair, robust (competitive), and consistent learning-augmented algorithm with substantial performance improvement in trace-driven experiments.
Online Search With Best-Price and Query-Based Predictions
Dec 02, 2021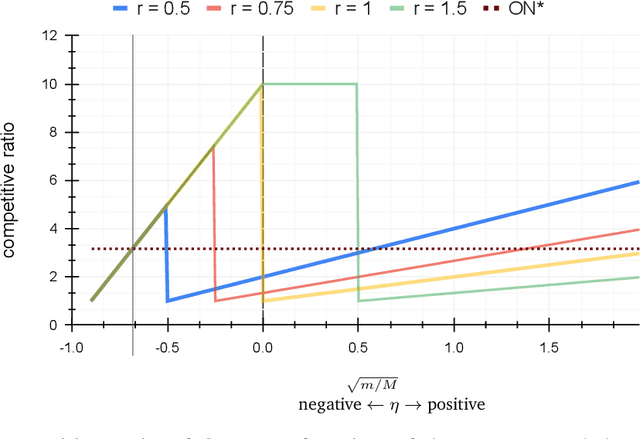
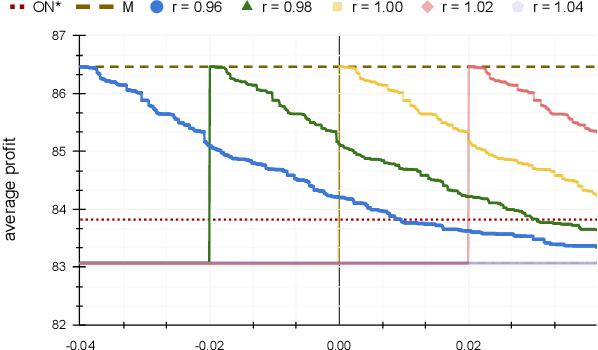
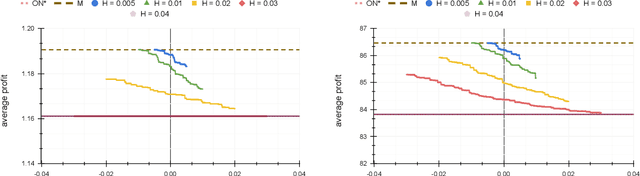
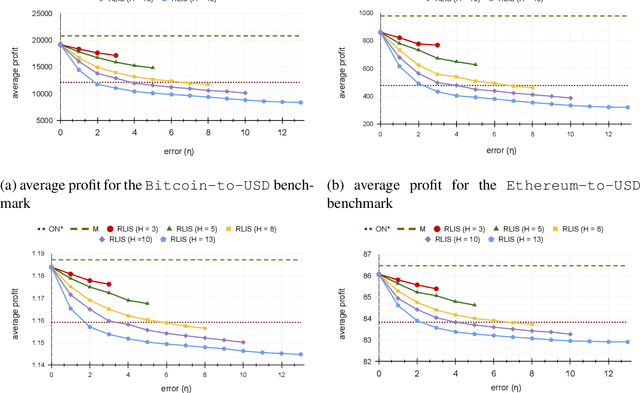
Abstract:In the online (time-series) search problem, a player is presented with a sequence of prices which are revealed in an online manner. In the standard definition of the problem, for each revealed price, the player must decide irrevocably whether to accept or reject it, without knowledge of future prices (other than an upper and a lower bound on their extreme values), and the objective is to minimize the competitive ratio, namely the worst-case ratio between the maximum price in the sequence and the one selected by the player. The problem formulates several applications of decision-making in the face of uncertainty on the revealed samples. Previous work on this problem has largely assumed extreme scenarios in which either the player has almost no information about the input, or the player is provided with some powerful, and error-free advice. In this work, we study learning-augmented algorithms, in which there is a potentially erroneous prediction concerning the input. Specifically, we consider two different settings: the setting in which the prediction is related to the maximum price in the sequence, as well as the setting in which the prediction is obtained as a response to a number of binary queries. For both settings, we provide tight, or near-tight upper and lower bounds on the worst-case performance of search algorithms as a function of the prediction error. We also provide experimental results on data obtained from stock exchange markets that confirm the theoretical analysis, and explain how our techniques can be applicable to other learning-augmented applications.
Online Bin Packing with Predictions
Feb 05, 2021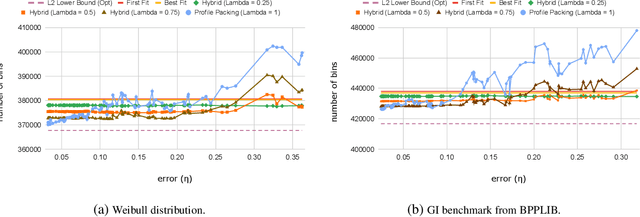
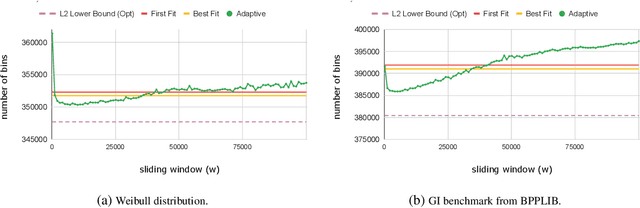
Abstract:Bin packing is a classic optimization problem with a wide range of applications from load balancing in networks to supply chain management. In this work we study the online variant of the problem, in which a sequence of items of various sizes must be placed into a minimum number of bins of uniform capacity. The online algorithm is enhanced with a (potentially erroneous) prediction concerning the frequency of item sizes in the sequence. We design and analyze online algorithms with efficient tradeoffs between their consistency (i.e., the competitive ratio assuming no prediction error) and their robustness (i.e., the competitive ratio under adversarial error), and whose performance degrades gently as a function of the error. Previous work on this problem has only addressed the extreme cases with respect to the prediction error, and has relied on overly powerful and error-free prediction oracles.
Contract Scheduling With Predictions
Nov 24, 2020

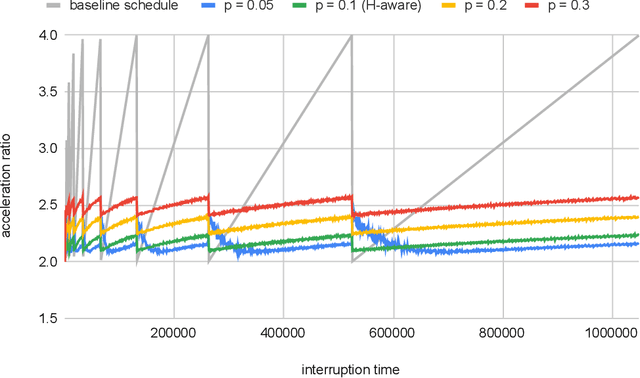

Abstract:Contract scheduling is a general technique that allows to design a system with interruptible capabilities, given an algorithm that is not necessarily interruptible. Previous work on this topic has largely assumed that the interruption is a worst-case deadline that is unknown to the scheduler. In this work, we study the setting in which there is a potentially erroneous prediction concerning the interruption. Specifically, we consider the setting in which the prediction describes the time that the interruption occurs, as well as the setting in which the prediction is obtained as a response to a single or multiple binary queries. For both settings, we investigate tradeoffs between the robustness (i.e., the worst-case performance assuming adversarial prediction) and the consistency (i.e, the performance assuming that the prediction is error-free), both from the side of positive and negative results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge