Interruptible Algorithms for Multiproblem Solving

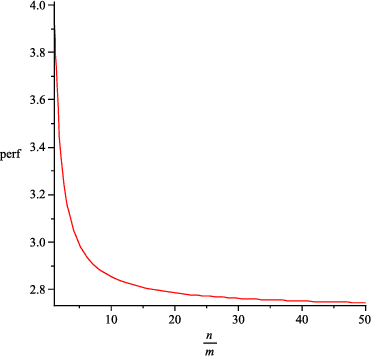
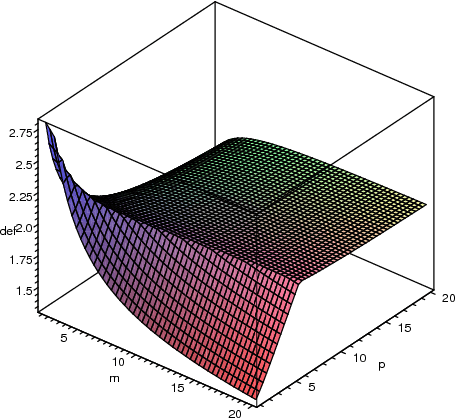
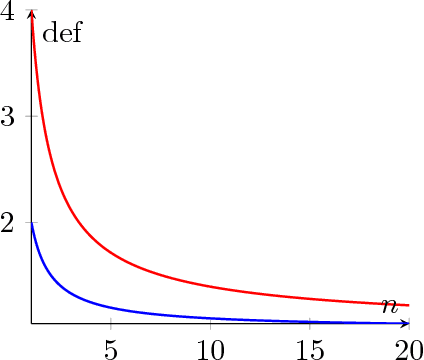
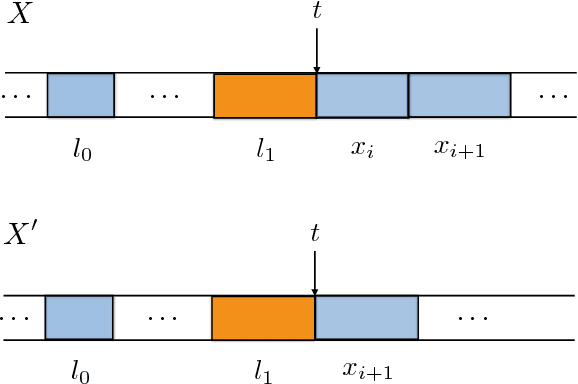
In this paper we address the problem of designing an interruptible system in a setting in which $n$ problem instances, all equally important, must be solved concurrently. The system involves scheduling executions of contract algorithms (which offer a trade-off between allowable computation time and quality of the solution) in m identical parallel processors. When an interruption occurs, the system must report a solution to each of the $n$ problem instances. The quality of this output is then compared to the best-possible algorithm that has foreknowledge of the interruption time and must, likewise, produce solutions to all $n$ problem instances. This extends the well-studied setting in which only one problem instance is queried at interruption time. In this work we first introduce new measures for evaluating the performance of interruptible systems in this setting. In particular, we propose the deficiency of a schedule as a performance measure that meets the requirements of the problem at hand. We then present a schedule whose performance we prove that is within a small factor from optimal in the general, multiprocessor setting. We also show several lower bounds on the deficiency of schedules on a single processor. More precisely, we prove a general lower bound of (n+1)/n, an improved lower bound for the two-problem setting (n=2), and a tight lower bound for the class of round-robin schedules. Our techniques can also yield a simpler, alternative proof of the main result of [Bernstein et al, IJCAI 2003] concerning the performance of cyclic schedules in multiprocessor environments.

Optimal Distributed Searching in the Plane with and without Uncertainty

We consider the problem of multiple agents or robots searching for a target in the plane. This is motivated by Search and Rescue operations (SAR) in the high seas which in the past were often performed with several vessels, and more recently by swarms of aerial drones and/or unmanned surface vessels. Coordinating such a search in an effective manner is a non trivial task. In this paper, we develop first an optimal strategy for searching with k robots starting from a common origin and moving at unit speed. We then apply the results from this model to more realistic scenarios such as differential search speeds, late arrival times to the search effort and low probability of detection under poor visibility conditions. We show that, surprisingly, the theoretical idealized model still governs the search with certain suitable minor adaptations.

Local Policies for Efficiently Patrolling a Triangulated Region by a Robot Swarm

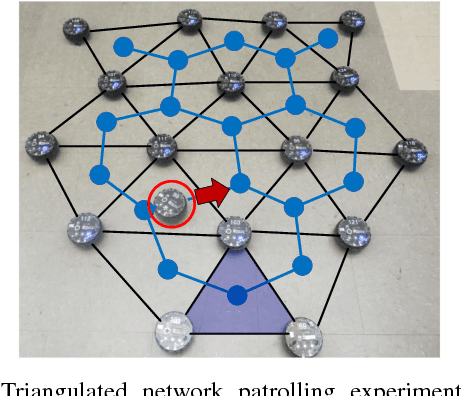
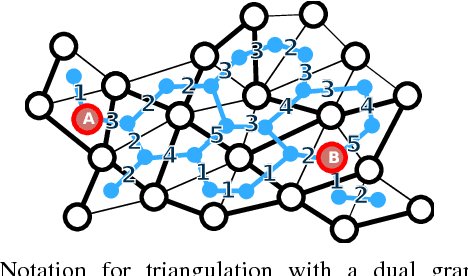
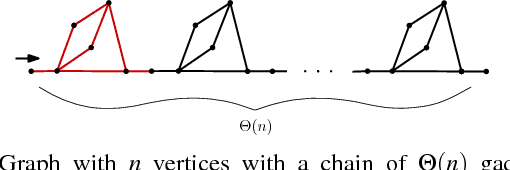
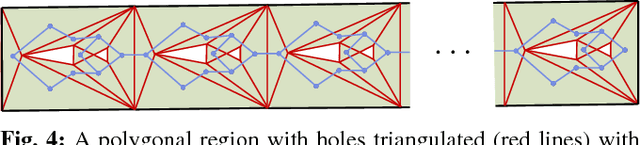
We present and analyze methods for patrolling an environment with a distributed swarm of robots. Our approach uses a physical data structure - a distributed triangulation of the workspace. A large number of stationary "mapping" robots cover and triangulate the environment and a smaller number of mobile "patrolling" robots move amongst them. The focus of this work is to develop, analyze, implement and compare local patrolling policies. We desire strategies that achieve full coverage, but also produce good coverage frequency and visitation times. Policies that provide theoretical guarantees for these quantities have received some attention, but gaps have remained. We present: 1) A summary of how to achieve coverage by building a triangulation of the workspace, and the ensuing properties. 2) A description of simple local policies (LRV, for Least Recently Visited and LFV, for Least Frequently Visited) for achieving coverage by the patrolling robots. 3) New analytical arguments why different versions of LRV may require worst case exponential time between visits of triangles. 4) Analytical evidence that a local implementation of LFV on the edges of the dual graph is possible in our scenario, and immensely better in the worst case. 5) Experimental and simulation validation for the practical usefulness of these policies, showing that even a small number of weak robots with weak local information can greatly outperform a single, powerful robots with full information and computational capabilities.