A Parallel Distributed Strategy for Arraying a Scattered Robot Swarm

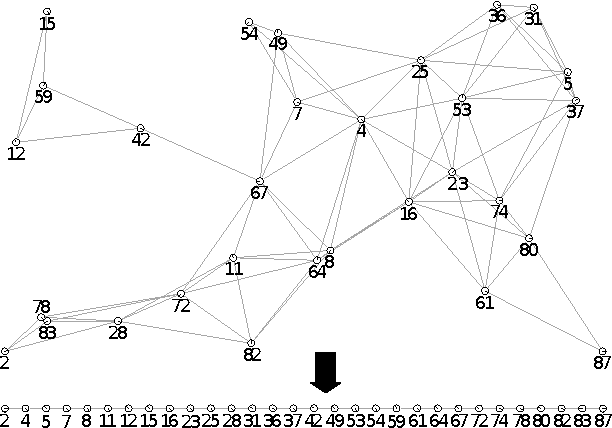
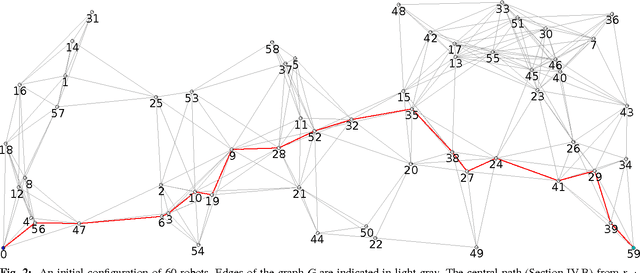
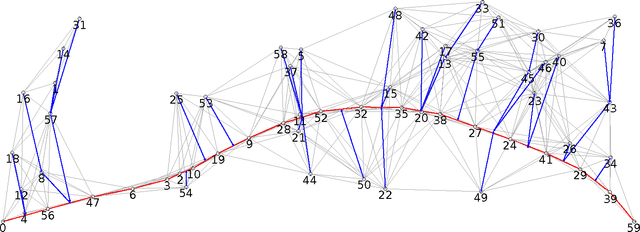
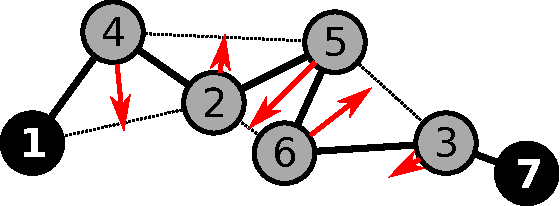
We consider the problem of organizing a scattered group of $n$ robots in two-dimensional space, with geometric maximum distance $D$ between robots. The communication graph of the swarm is connected, but there is no central authority for organizing it. We want to arrange them into a sorted and equally-spaced array between the robots with lowest and highest label, while maintaining a connected communication network. In this paper, we describe a distributed method to accomplish these goals, without using central control, while also keeping time, travel distance and communication cost at a minimum. We proceed in a number of stages (leader election, initial path construction, subtree contraction, geometric straightening, and distributed sorting), none of which requires a central authority, but still accomplishes best possible parallelization. The overall arraying is performed in $O(n)$ time, $O(n^2)$ individual messages, and $O(nD)$ travel distance. Implementation of the sorting and navigation use communication messages of fixed size, and are a practical solution for large populations of low-cost robots.

Local Policies for Efficiently Patrolling a Triangulated Region by a Robot Swarm

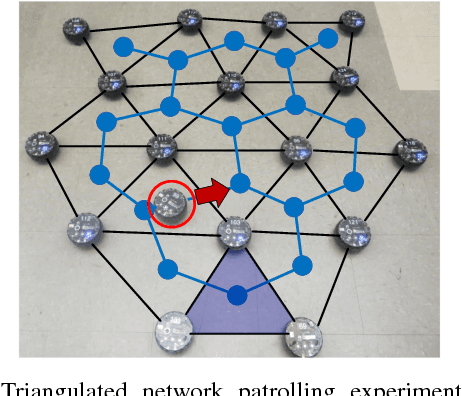
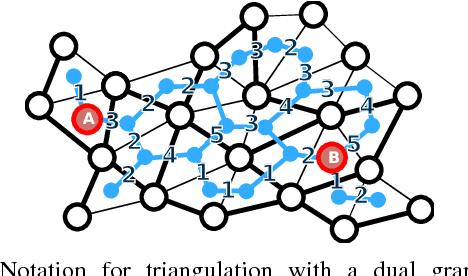
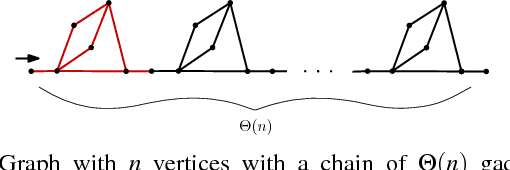
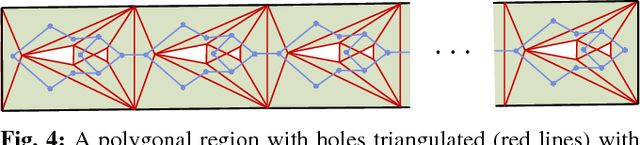
We present and analyze methods for patrolling an environment with a distributed swarm of robots. Our approach uses a physical data structure - a distributed triangulation of the workspace. A large number of stationary "mapping" robots cover and triangulate the environment and a smaller number of mobile "patrolling" robots move amongst them. The focus of this work is to develop, analyze, implement and compare local patrolling policies. We desire strategies that achieve full coverage, but also produce good coverage frequency and visitation times. Policies that provide theoretical guarantees for these quantities have received some attention, but gaps have remained. We present: 1) A summary of how to achieve coverage by building a triangulation of the workspace, and the ensuing properties. 2) A description of simple local policies (LRV, for Least Recently Visited and LFV, for Least Frequently Visited) for achieving coverage by the patrolling robots. 3) New analytical arguments why different versions of LRV may require worst case exponential time between visits of triangles. 4) Analytical evidence that a local implementation of LFV on the edges of the dual graph is possible in our scenario, and immensely better in the worst case. 5) Experimental and simulation validation for the practical usefulness of these policies, showing that even a small number of weak robots with weak local information can greatly outperform a single, powerful robots with full information and computational capabilities.

Particle Computation: Designing Worlds to Control Robot Swarms with only Global Signals

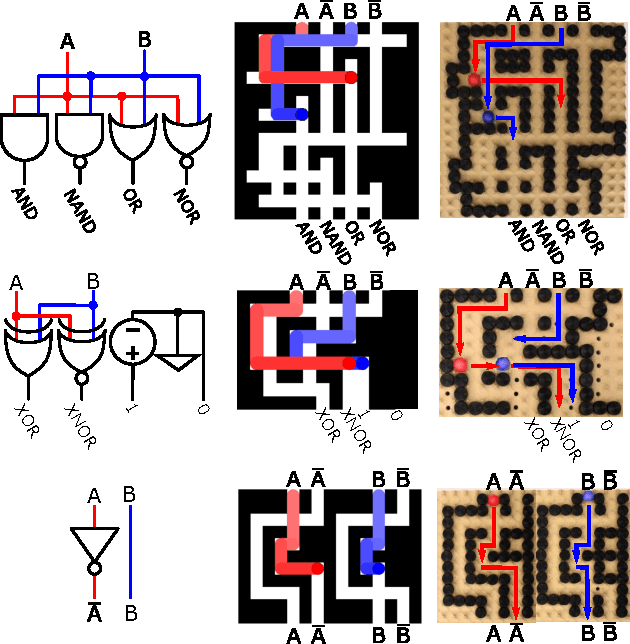
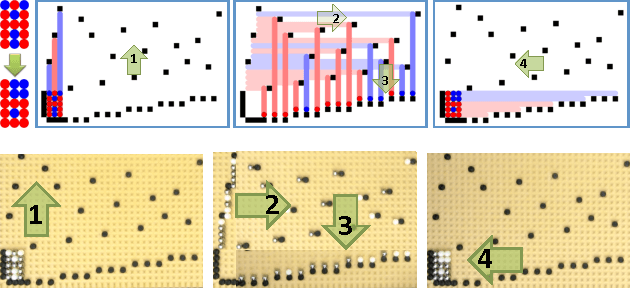
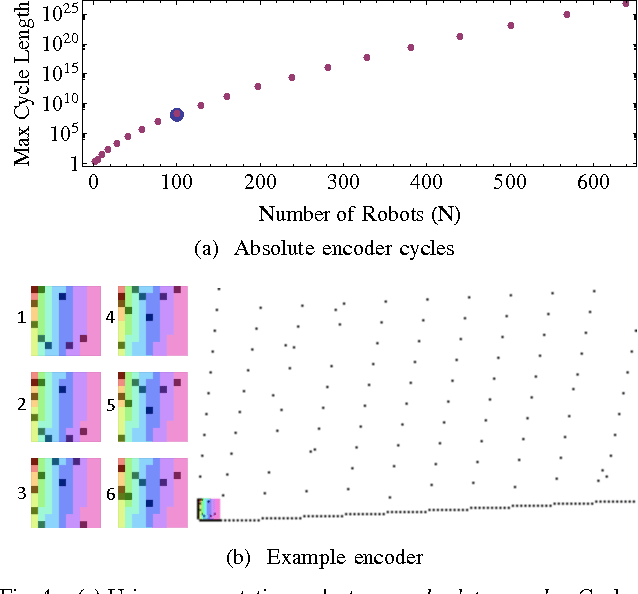
Micro- and nanorobots are often controlled by global input signals, such as an electromagnetic or gravitational field. These fields move each robot maximally until it hits a stationary obstacle or another stationary robot. This paper investigates 2D motion-planning complexity for large swarms of simple mobile robots (such as bacteria, sensors, or smart building material). In previous work we proved it is NP-hard to decide whether a given initial configuration can be transformed into a desired target configuration; in this paper we prove a stronger result: the problem of finding an optimal control sequence is PSPACE-complete. On the positive side, we show we can build useful systems by designing obstacles. We present a reconfigurable hardware platform and demonstrate how to form arbitrary permutations and build a compact absolute encoder. We then take the same platform and use dual-rail logic to build a universal logic gate that concurrently evaluates AND, NAND, NOR and OR operations. Using many of these gates and appropriate interconnects we can evaluate any logical expression.

Crowdsourcing Swarm Manipulation Experiments: A Massive Online User Study with Large Swarms of Simple Robots

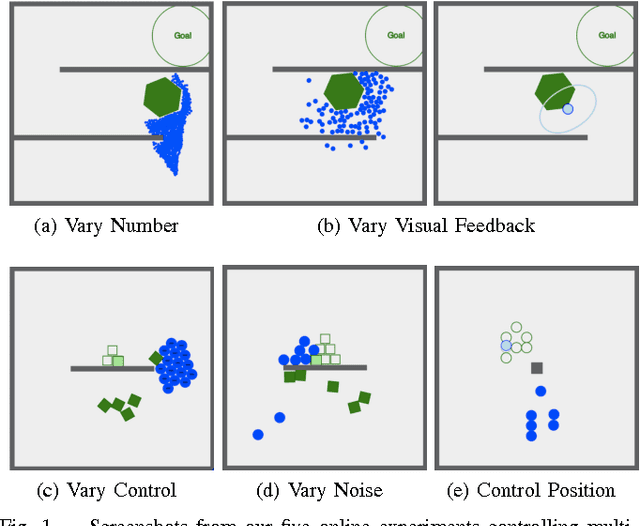
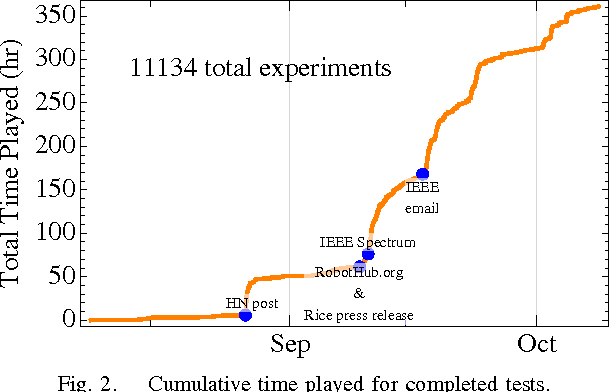
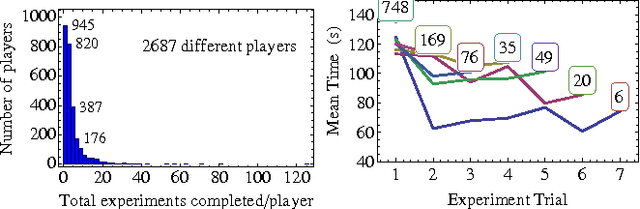
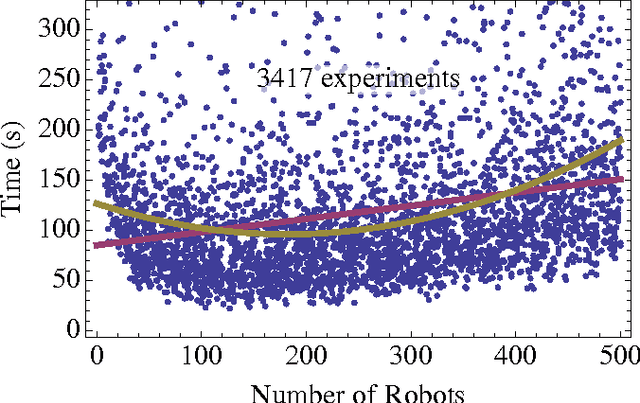
Micro- and nanorobotics have the potential to revolutionize many applications including targeted material delivery, assembly, and surgery. The same properties that promise breakthrough solutions---small size and large populations---present unique challenges to generating controlled motion. We want to use large swarms of robots to perform manipulation tasks; unfortunately, human-swarm interaction studies as conducted today are limited in sample size, are difficult to reproduce, and are prone to hardware failures. We present an alternative. This paper examines the perils, pitfalls, and possibilities we discovered by launching SwarmControl.net, an online game where players steer swarms of up to 500 robots to complete manipulation challenges. We record statistics from thousands of players, and use the game to explore aspects of large-population robot control. We present the game framework as a new, open-source tool for large-scale user experiments. Our results have potential applications in human control of micro- and nanorobots, supply insight for automatic controllers, and provide a template for large online robotic research experiments.

Exploration via Structured Triangulation by a Multi-Robot System with Bearing-Only Low-Resolution Sensors

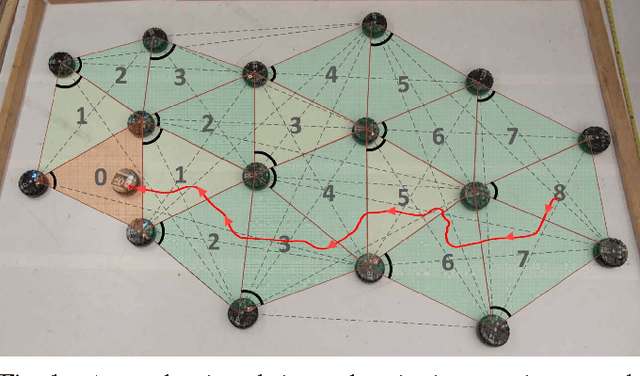
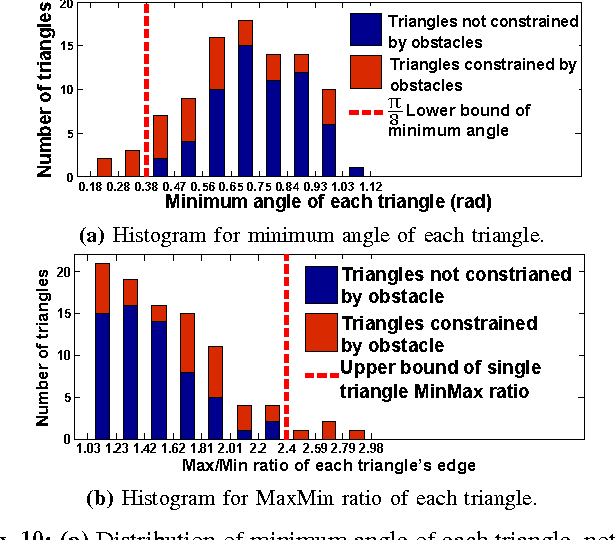
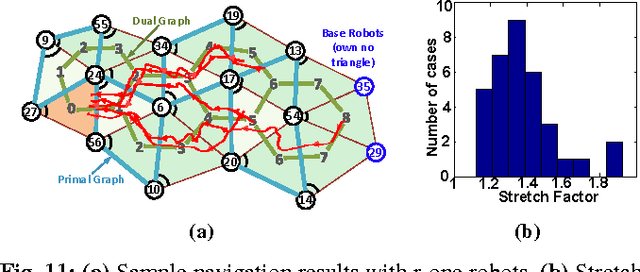
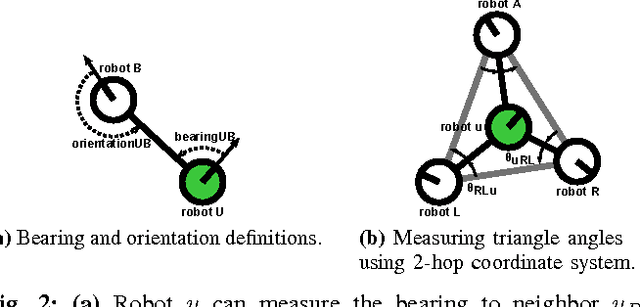
This paper presents a distributed approach for exploring and triangulating an unknown region using a multi- robot system. The objective is to produce a covering of an unknown workspace by a fixed number of robots such that the covered region is maximized, solving the Maximum Area Triangulation Problem (MATP). The resulting triangulation is a physical data structure that is a compact representation of the workspace; it contains distributed knowledge of each triangle, adjacent triangles, and the dual graph of the workspace. Algorithms can store information in this physical data structure, such as a routing table for robot navigation Our algorithm builds a triangulation in a closed environment, starting from a single location. It provides coverage with a breadth-first search pattern and completeness guarantees. We show the computational and communication requirements to build and maintain the triangulation and its dual graph are small. Finally, we present a physical navigation algorithm that uses the dual graph, and show that the resulting path lengths are within a constant factor of the shortest-path Euclidean distance. We validate our theoretical results with experiments on triangulating a region with a system of low-cost robots. Analysis of the resulting quality of the triangulation shows that most of the triangles are of high quality, and cover a large area. Implementation of the triangulation, dual graph, and navigation all use communication messages of fixed size, and are a practical solution for large populations of low-cost robots.