A Parallel Distributed Strategy for Arraying a Scattered Robot Swarm

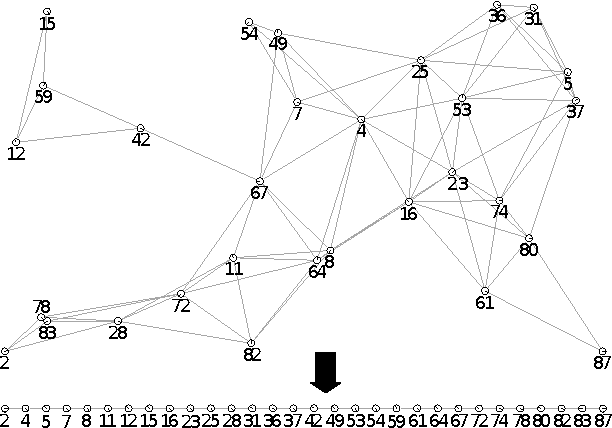
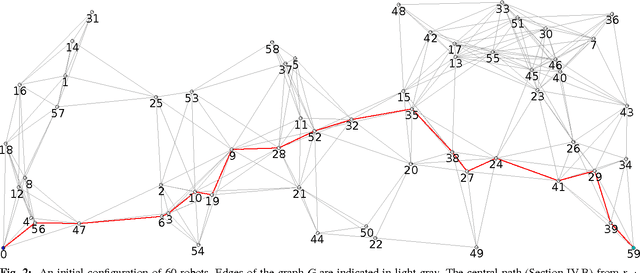
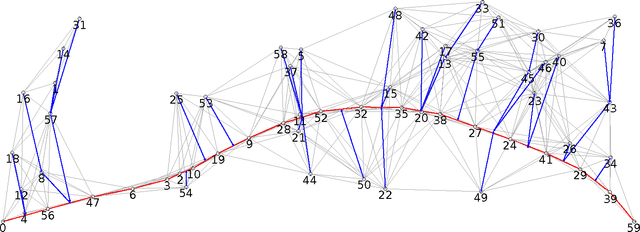
We consider the problem of organizing a scattered group of $n$ robots in two-dimensional space, with geometric maximum distance $D$ between robots. The communication graph of the swarm is connected, but there is no central authority for organizing it. We want to arrange them into a sorted and equally-spaced array between the robots with lowest and highest label, while maintaining a connected communication network. In this paper, we describe a distributed method to accomplish these goals, without using central control, while also keeping time, travel distance and communication cost at a minimum. We proceed in a number of stages (leader election, initial path construction, subtree contraction, geometric straightening, and distributed sorting), none of which requires a central authority, but still accomplishes best possible parallelization. The overall arraying is performed in $O(n)$ time, $O(n^2)$ individual messages, and $O(nD)$ travel distance. Implementation of the sorting and navigation use communication messages of fixed size, and are a practical solution for large populations of low-cost robots.

Distributed Cohesive Control for Robot Swarms: Maintaining Good Connectivity in the Presence of Exterior Forces

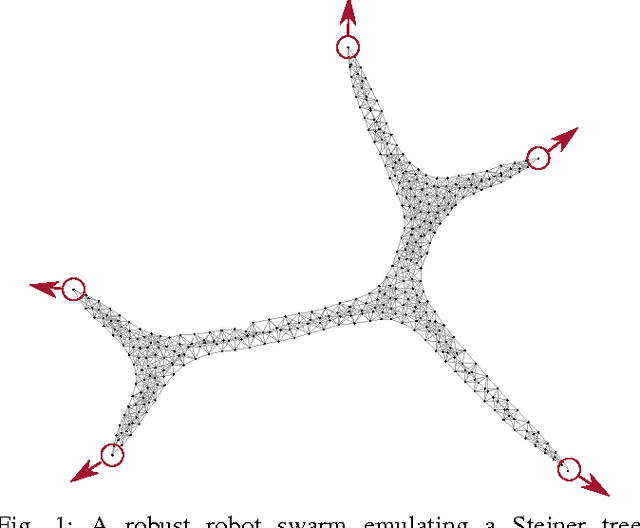
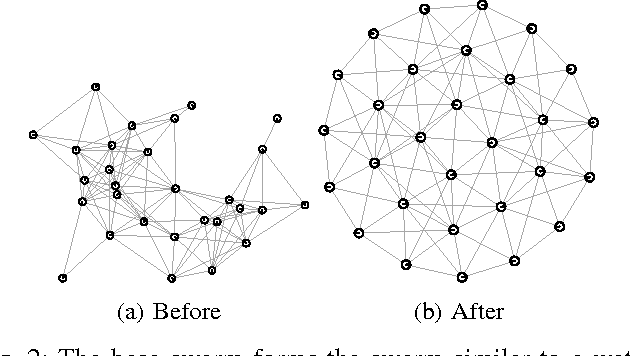
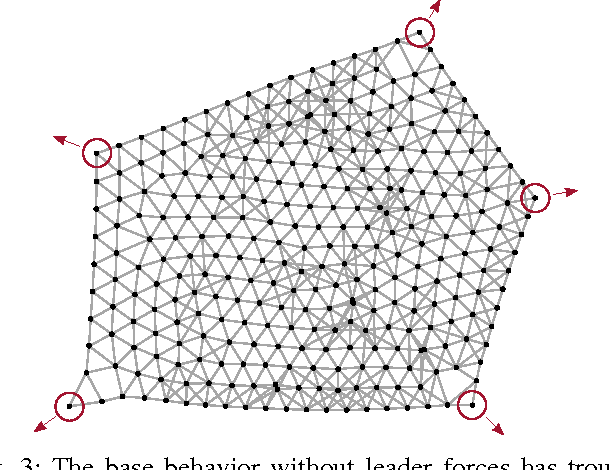
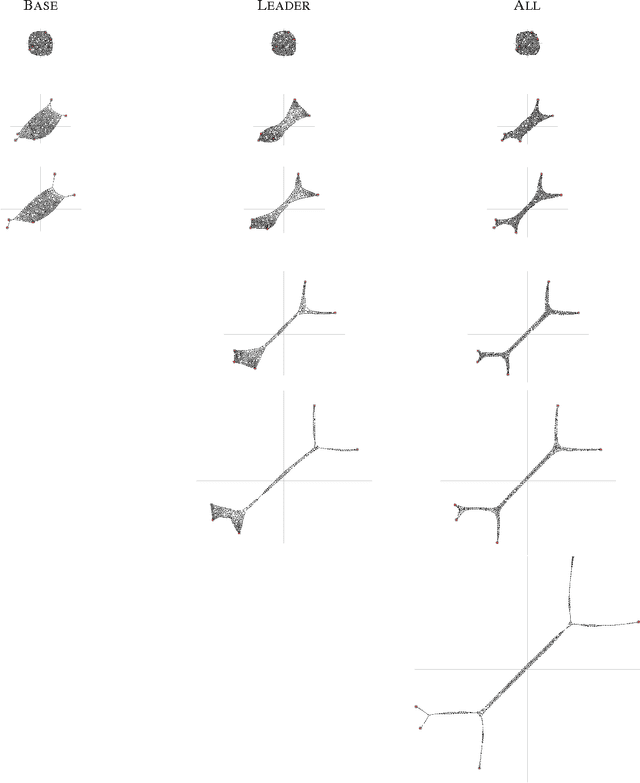
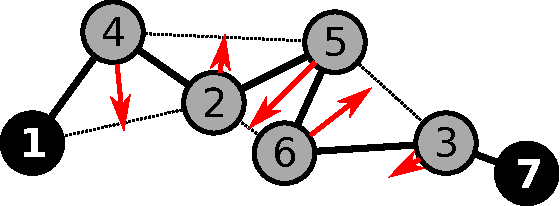
We present a number of powerful local mechanisms for maintaining a dynamic swarm of robots with limited capabilities and information, in the presence of external forces and permanent node failures. We propose a set of local continuous algorithms that together produce a generalization of a Euclidean Steiner tree. At any stage, the resulting overall shape achieves a good compromise between local thickness, global connectivity, and flexibility to further continuous motion of the terminals. The resulting swarm behavior scales well, is robust against node failures, and performs close to the best known approximation bound for a corresponding centralized static optimization problem.

On the Power of Manifold Samples in Exploring Configuration Spaces and the Dimensionality of Narrow Passages

We extend our study of Motion Planning via Manifold Samples (MMS), a general algorithmic framework that combines geometric methods for the exact and complete analysis of low-dimensional configuration spaces with sampling-based approaches that are appropriate for higher dimensions. The framework explores the configuration space by taking samples that are entire low-dimensional manifolds of the configuration space capturing its connectivity much better than isolated point samples. The contributions of this paper are as follows: (i) We present a recursive application of MMS in a six-dimensional configuration space, enabling the coordination of two polygonal robots translating and rotating amidst polygonal obstacles. In the adduced experiments for the more demanding test cases MMS clearly outperforms PRM, with over 20-fold speedup in a coordination-tight setting. (ii) A probabilistic completeness proof for the most prevalent case, namely MMS with samples that are affine subspaces. (iii) A closer examination of the test cases reveals that MMS has, in comparison to standard sampling-based algorithms, a significant advantage in scenarios containing high-dimensional narrow passages. This provokes a novel characterization of narrow passages which attempts to capture their dimensionality, an attribute that had been (to a large extent) unattended in previous definitions.

Motion Planning via Manifold Samples

We present a general and modular algorithmic framework for path planning of robots. Our framework combines geometric methods for exact and complete analysis of low-dimensional configuration spaces, together with practical, considerably simpler sampling-based approaches that are appropriate for higher dimensions. In order to facilitate the transfer of advanced geometric algorithms into practical use, we suggest taking samples that are entire low-dimensional manifolds of the configuration space that capture the connectivity of the configuration space much better than isolated point samples. Geometric algorithms for analysis of low-dimensional manifolds then provide powerful primitive operations. The modular design of the framework enables independent optimization of each modular component. Indeed, we have developed, implemented and optimized a primitive operation for complete and exact combinatorial analysis of a certain set of manifolds, using arrangements of curves of rational functions and concepts of generic programming. This in turn enabled us to implement our framework for the concrete case of a polygonal robot translating and rotating amidst polygonal obstacles. We demonstrate that the integration of several carefully engineered components leads to significant speedup over the popular PRM sampling-based algorithm, which represents the more simplistic approach that is prevalent in practice. We foresee possible extensions of our framework to solving high-dimensional problems beyond motion planning.