A Parallel Distributed Strategy for Arraying a Scattered Robot Swarm

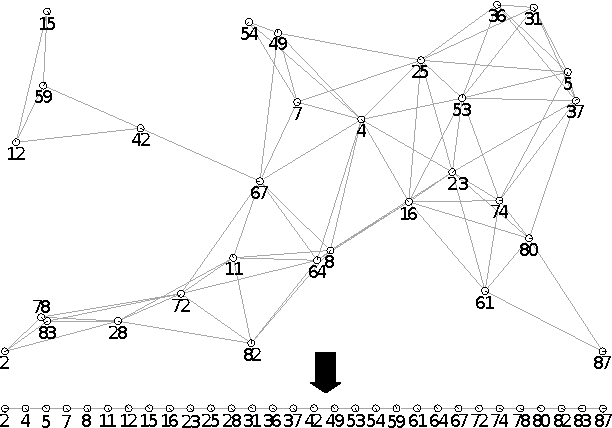
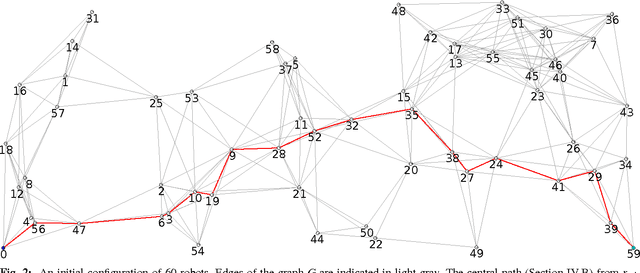
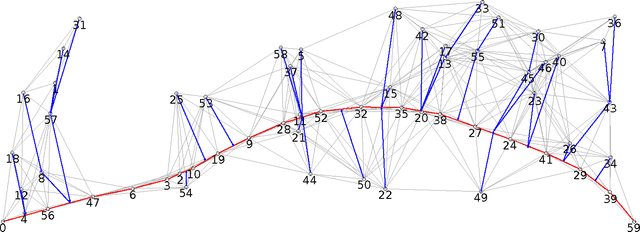
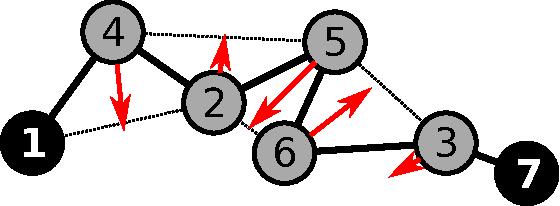
We consider the problem of organizing a scattered group of $n$ robots in two-dimensional space, with geometric maximum distance $D$ between robots. The communication graph of the swarm is connected, but there is no central authority for organizing it. We want to arrange them into a sorted and equally-spaced array between the robots with lowest and highest label, while maintaining a connected communication network. In this paper, we describe a distributed method to accomplish these goals, without using central control, while also keeping time, travel distance and communication cost at a minimum. We proceed in a number of stages (leader election, initial path construction, subtree contraction, geometric straightening, and distributed sorting), none of which requires a central authority, but still accomplishes best possible parallelization. The overall arraying is performed in $O(n)$ time, $O(n^2)$ individual messages, and $O(nD)$ travel distance. Implementation of the sorting and navigation use communication messages of fixed size, and are a practical solution for large populations of low-cost robots.

Distributed Cohesive Control for Robot Swarms: Maintaining Good Connectivity in the Presence of Exterior Forces

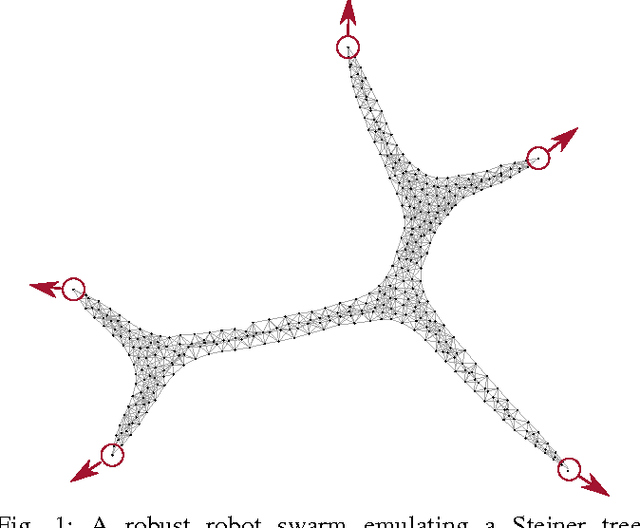
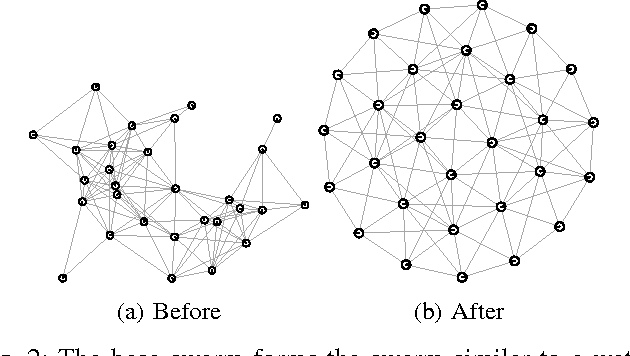
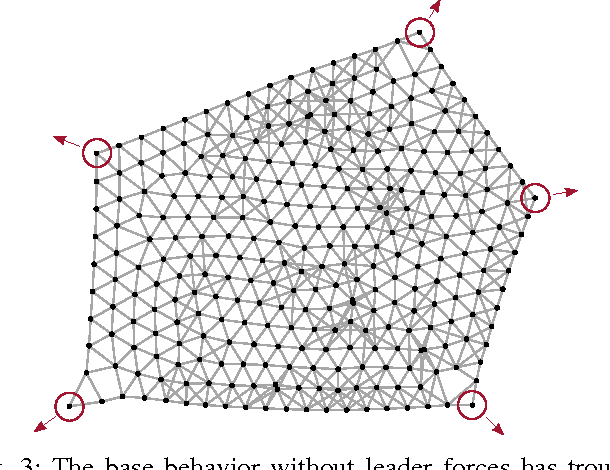
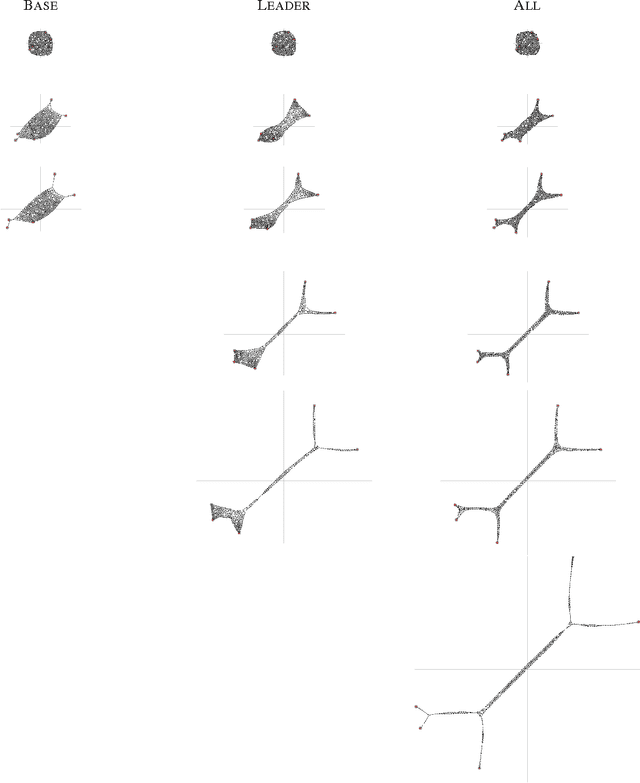
We present a number of powerful local mechanisms for maintaining a dynamic swarm of robots with limited capabilities and information, in the presence of external forces and permanent node failures. We propose a set of local continuous algorithms that together produce a generalization of a Euclidean Steiner tree. At any stage, the resulting overall shape achieves a good compromise between local thickness, global connectivity, and flexibility to further continuous motion of the terminals. The resulting swarm behavior scales well, is robust against node failures, and performs close to the best known approximation bound for a corresponding centralized static optimization problem.

Local Policies for Efficiently Patrolling a Triangulated Region by a Robot Swarm

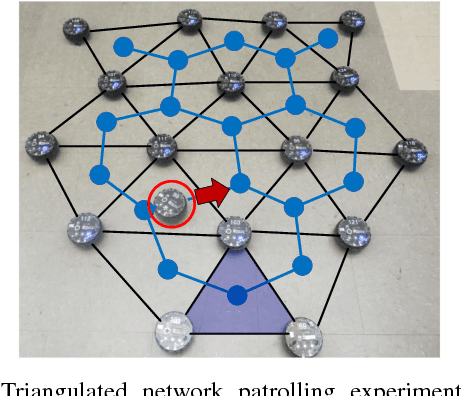
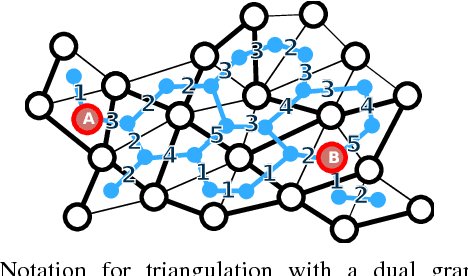
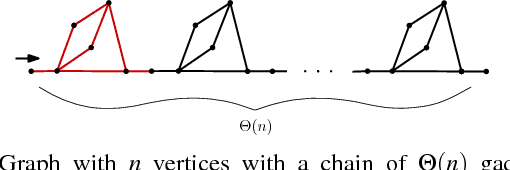
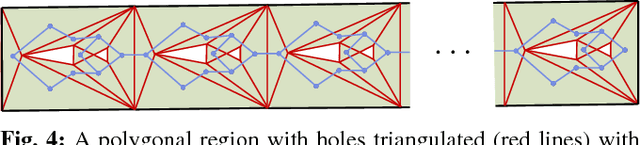
We present and analyze methods for patrolling an environment with a distributed swarm of robots. Our approach uses a physical data structure - a distributed triangulation of the workspace. A large number of stationary "mapping" robots cover and triangulate the environment and a smaller number of mobile "patrolling" robots move amongst them. The focus of this work is to develop, analyze, implement and compare local patrolling policies. We desire strategies that achieve full coverage, but also produce good coverage frequency and visitation times. Policies that provide theoretical guarantees for these quantities have received some attention, but gaps have remained. We present: 1) A summary of how to achieve coverage by building a triangulation of the workspace, and the ensuing properties. 2) A description of simple local policies (LRV, for Least Recently Visited and LFV, for Least Frequently Visited) for achieving coverage by the patrolling robots. 3) New analytical arguments why different versions of LRV may require worst case exponential time between visits of triangles. 4) Analytical evidence that a local implementation of LFV on the edges of the dual graph is possible in our scenario, and immensely better in the worst case. 5) Experimental and simulation validation for the practical usefulness of these policies, showing that even a small number of weak robots with weak local information can greatly outperform a single, powerful robots with full information and computational capabilities.

A Protocol for Self-Synchronized Duty-Cycling in Sensor Networks: Generic Implementation in Wiselib

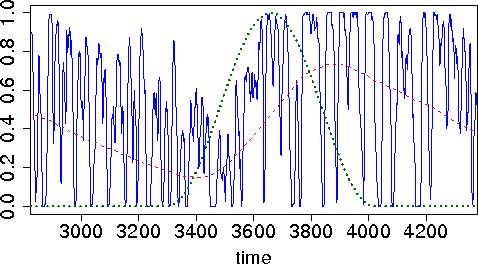
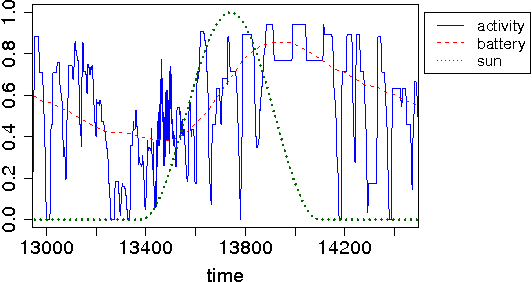
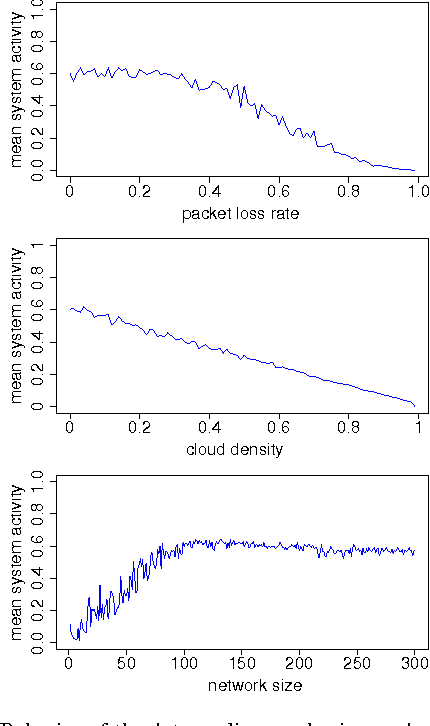
In this work we present a protocol for self-synchronized duty-cycling in wireless sensor networks with energy harvesting capabilities. The protocol is implemented in Wiselib, a library of generic algorithms for sensor networks. Simulations are conducted with the sensor network simulator Shawn. They are based on the specifications of real hardware known as iSense sensor nodes. The experimental results show that the proposed mechanism is able to adapt to changing energy availabilities. Moreover, it is shown that the system is very robust against packet loss.

Polygon Exploration with Time-Discrete Vision

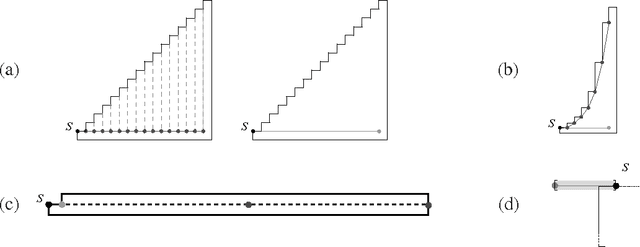
With the advent of autonomous robots with two- and three-dimensional scanning capabilities, classical visibility-based exploration methods from computational geometry have gained in practical importance. However, real-life laser scanning of useful accuracy does not allow the robot to scan continuously while in motion; instead, it has to stop each time it surveys its environment. This requirement was studied by Fekete, Klein and Nuechter for the subproblem of looking around a corner, but until now has not been considered in an online setting for whole polygonal regions. We give the first algorithmic results for this important algorithmic problem that combines stationary art gallery-type aspects with watchman-type issues in an online scenario: We demonstrate that even for orthoconvex polygons, a competitive strategy can be achieved only for limited aspect ratio A (the ratio of the maximum and minimum edge length of the polygon), i.e., for a given lower bound on the size of an edge; we give a matching upper bound by providing an O(log A)-competitive strategy for simple rectilinear polygons, using the assumption that each edge of the polygon has to be fully visible from some scan point.

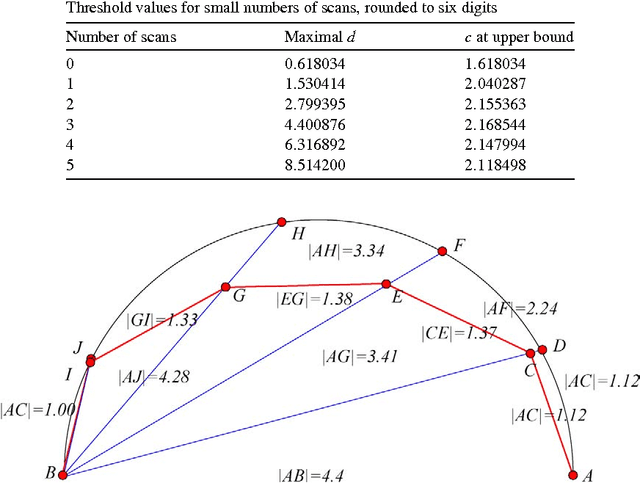
Online Searching with an Autonomous Robot

We discuss online strategies for visibility-based searching for an object hidden behind a corner, using Kurt3D, a real autonomous mobile robot. This task is closely related to a number of well-studied problems. Our robot uses a three-dimensional laser scanner in a stop, scan, plan, go fashion for building a virtual three-dimensional environment. Besides planning trajectories and avoiding obstacles, Kurt3D is capable of identifying objects like a chair. We derive a practically useful and asymptotically optimal strategy that guarantees a competitive ratio of 2, which differs remarkably from the well-studied scenario without the need of stopping for surveying the environment. Our strategy is used by Kurt3D, documented in a separate video.

Algorithms for Rapidly Dispersing Robot Swarms in Unknown Environments

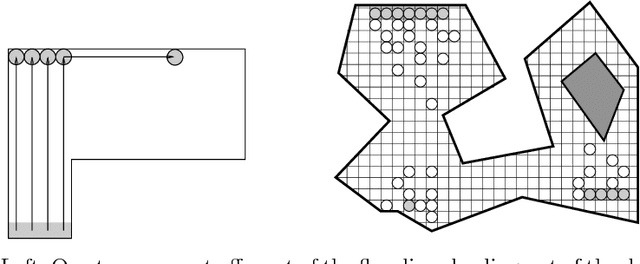
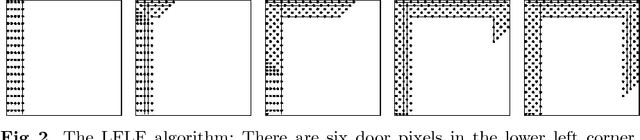
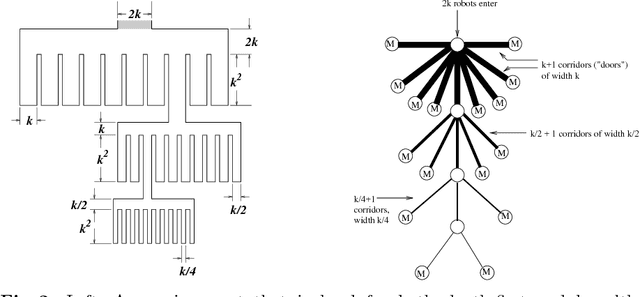
We develop and analyze algorithms for dispersing a swarm of primitive robots in an unknown environment, R. The primary objective is to minimize the makespan, that is, the time to fill the entire region. An environment is composed of pixels that form a connected subset of the integer grid. There is at most one robot per pixel and robots move horizontally or vertically at unit speed. Robots enter R by means of k>=1 door pixels Robots are primitive finite automata, only having local communication, local sensors, and a constant-sized memory. We first give algorithms for the single-door case (i.e., k=1), analyzing the algorithms both theoretically and experimentally. We prove that our algorithms have optimal makespan 2A-1, where A is the area of R. We next give an algorithm for the multi-door case (k>1), based on a wall-following version of the leader-follower strategy. We prove that our strategy is O(log(k+1))-competitive, and that this bound is tight for our strategy and other related strategies.