Universal Reconfiguration of Facet-Connected Modular Robots by Pivots: The $O(1)$ Musketeers

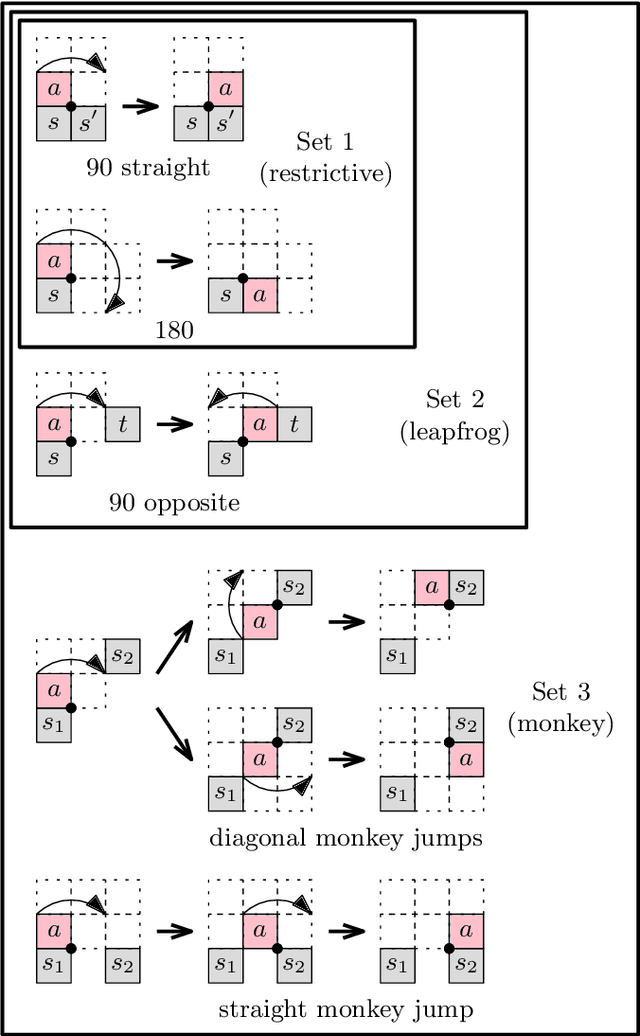
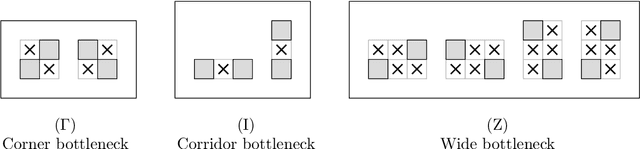
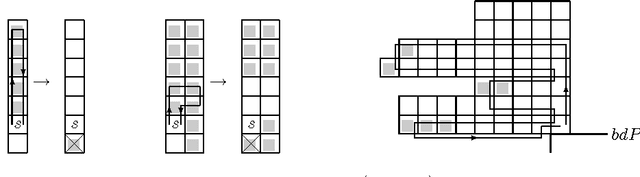
We present the first universal reconfiguration algorithm for transforming a modular robot between any two facet-connected square-grid configurations using pivot moves. More precisely, we show that five extra "helper" modules ("musketeers") suffice to reconfigure the remaining $n$ modules between any two given configurations. Our algorithm uses $O(n^2)$ pivot moves, which is worst-case optimal. Previous reconfiguration algorithms either require less restrictive "sliding" moves, do not preserve facet-connectivity, or for the setting we consider, could only handle a small subset of configurations defined by a local forbidden pattern. Configurations with the forbidden pattern do have disconnected reconfiguration graphs (discrete configuration spaces), and indeed we show that they can have an exponential number of connected components. But forbidding the local pattern throughout the configuration is far from necessary, as we show that just a constant number of added modules (placed to be freely reconfigurable) suffice for universal reconfigurability. We also classify three different models of natural pivot moves that preserve facet-connectivity, and show separations between these models.

The Snowblower Problem

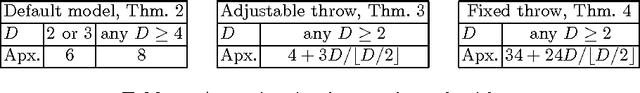
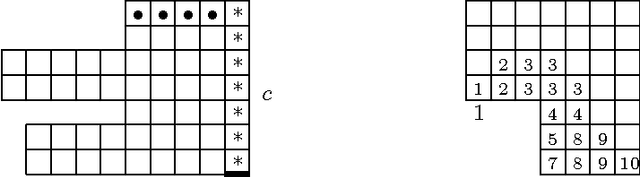
We introduce the snowblower problem (SBP), a new optimization problem that is closely related to milling problems and to some material-handling problems. The objective in the SBP is to compute a short tour for the snowblower to follow to remove all the snow from a domain (driveway, sidewalk, etc.). When a snowblower passes over each region along the tour, it displaces snow into a nearby region. The constraint is that if the snow is piled too high, then the snowblower cannot clear the pile. We give an algorithmic study of the SBP. We show that in general, the problem is NP-complete, and we present polynomial-time approximation algorithms for removing snow under various assumptions about the operation of the snowblower. Most commercially-available snowblowers allow the user to control the direction in which the snow is thrown. We differentiate between the cases in which the snow can be thrown in any direction, in any direction except backwards, and only to the right. For all cases, we give constant-factor approximation algorithms; the constants increase as the throw direction becomes more restricted. Our results are also applicable to robotic vacuuming (or lawnmowing) with bounded capacity dust bin and to some versions of material-handling problems, in which the goal is to rearrange cartons on the floor of a warehouse.

Algorithms for Rapidly Dispersing Robot Swarms in Unknown Environments

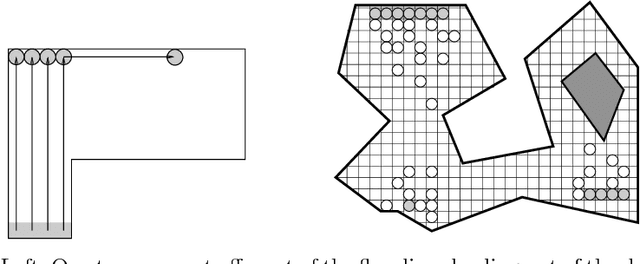
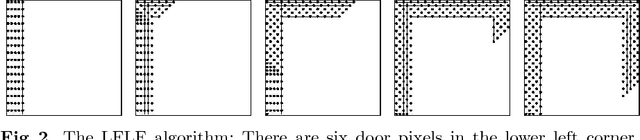
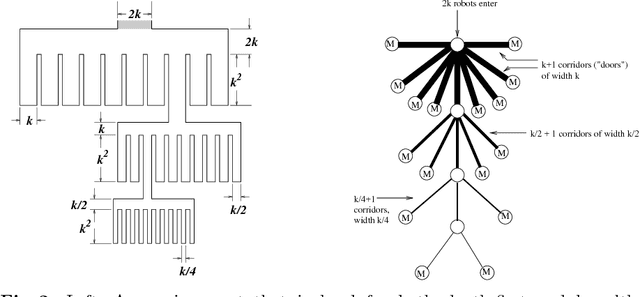
We develop and analyze algorithms for dispersing a swarm of primitive robots in an unknown environment, R. The primary objective is to minimize the makespan, that is, the time to fill the entire region. An environment is composed of pixels that form a connected subset of the integer grid. There is at most one robot per pixel and robots move horizontally or vertically at unit speed. Robots enter R by means of k>=1 door pixels Robots are primitive finite automata, only having local communication, local sensors, and a constant-sized memory. We first give algorithms for the single-door case (i.e., k=1), analyzing the algorithms both theoretically and experimentally. We prove that our algorithms have optimal makespan 2A-1, where A is the area of R. We next give an algorithm for the multi-door case (k>1), based on a wall-following version of the leader-follower strategy. We prove that our strategy is O(log(k+1))-competitive, and that this bound is tight for our strategy and other related strategies.