Universal Reconfiguration of Facet-Connected Modular Robots by Pivots: The $O(1)$ Musketeers

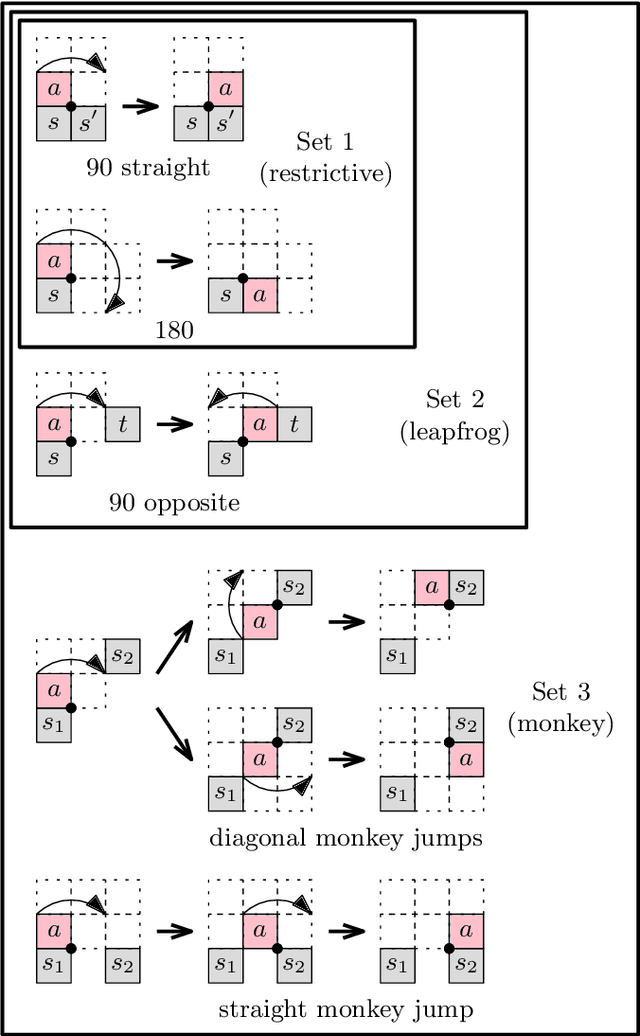
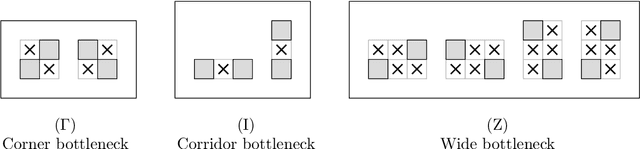
We present the first universal reconfiguration algorithm for transforming a modular robot between any two facet-connected square-grid configurations using pivot moves. More precisely, we show that five extra "helper" modules ("musketeers") suffice to reconfigure the remaining $n$ modules between any two given configurations. Our algorithm uses $O(n^2)$ pivot moves, which is worst-case optimal. Previous reconfiguration algorithms either require less restrictive "sliding" moves, do not preserve facet-connectivity, or for the setting we consider, could only handle a small subset of configurations defined by a local forbidden pattern. Configurations with the forbidden pattern do have disconnected reconfiguration graphs (discrete configuration spaces), and indeed we show that they can have an exponential number of connected components. But forbidding the local pattern throughout the configuration is far from necessary, as we show that just a constant number of added modules (placed to be freely reconfigurable) suffice for universal reconfigurability. We also classify three different models of natural pivot moves that preserve facet-connectivity, and show separations between these models.

Collective Construction of 2D Block Structures with Holes

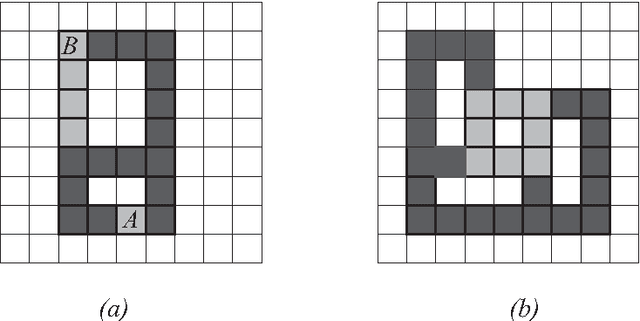
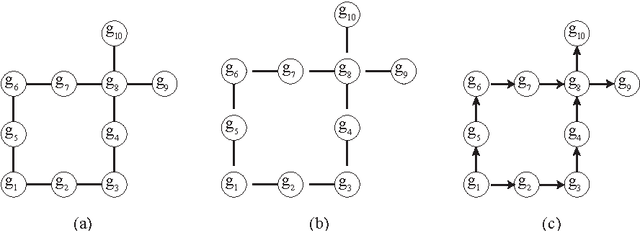
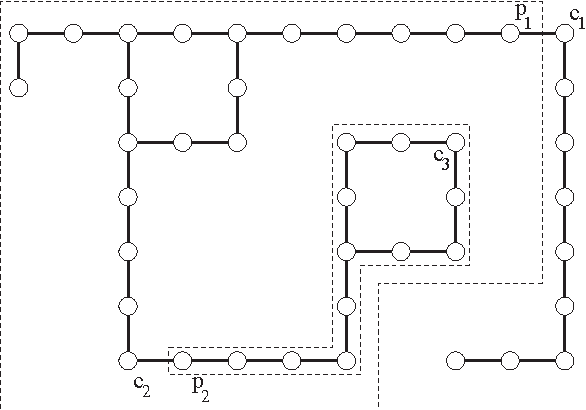
In this paper we present algorithms for collective construction systems in which a large number of autonomous mobile robots trans- port modular building elements to construct a desired structure. We focus on building block structures subject to some physical constraints that restrict the order in which the blocks may be attached to the structure. Specifically, we determine a partial ordering on the blocks such that if they are attached in accordance with this ordering, then (i) the structure is a single, connected piece at all intermediate stages of construction, and (ii) no block is attached between two other previously attached blocks, since such a space is too narrow for a robot to maneuver a block into it. Previous work has consider this problem for building 2D structures without holes. Here we extend this work to 2D structures with holes. We accomplish this by modeling the problem as a graph orientation problem and describe an O(n^2) algorithm for solving it. We also describe how this partial ordering may be used in a distributed fashion by the robots to coordinate their actions during the building process.