Collective Construction of 2D Block Structures with Holes

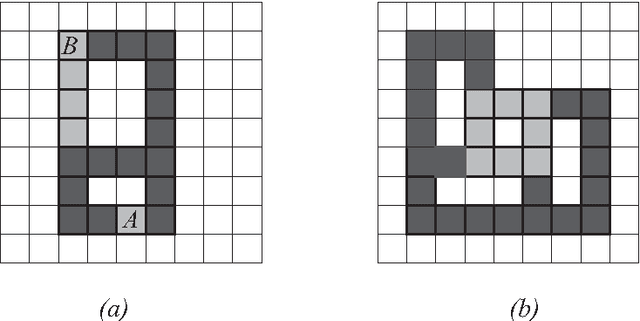
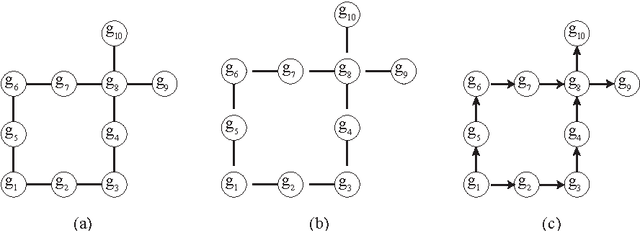
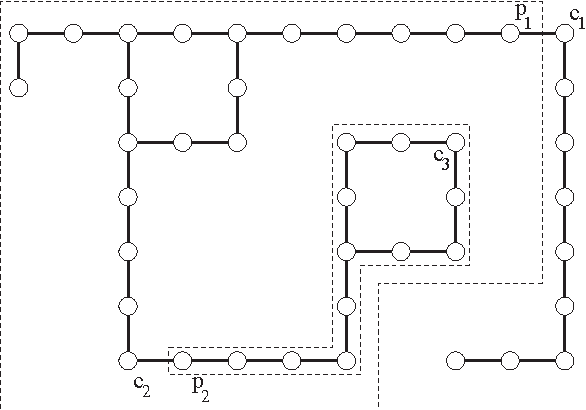
In this paper we present algorithms for collective construction systems in which a large number of autonomous mobile robots trans- port modular building elements to construct a desired structure. We focus on building block structures subject to some physical constraints that restrict the order in which the blocks may be attached to the structure. Specifically, we determine a partial ordering on the blocks such that if they are attached in accordance with this ordering, then (i) the structure is a single, connected piece at all intermediate stages of construction, and (ii) no block is attached between two other previously attached blocks, since such a space is too narrow for a robot to maneuver a block into it. Previous work has consider this problem for building 2D structures without holes. Here we extend this work to 2D structures with holes. We accomplish this by modeling the problem as a graph orientation problem and describe an O(n^2) algorithm for solving it. We also describe how this partial ordering may be used in a distributed fashion by the robots to coordinate their actions during the building process.