Algorithms for Rapidly Dispersing Robot Swarms in Unknown Environments
Paper and Code
Dec 10, 2002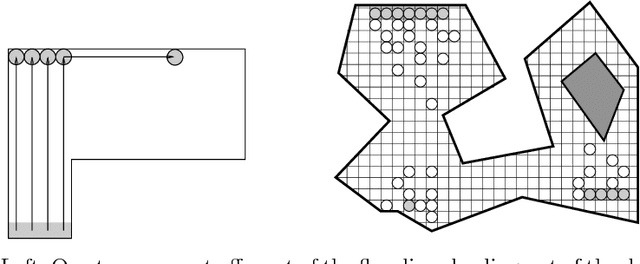
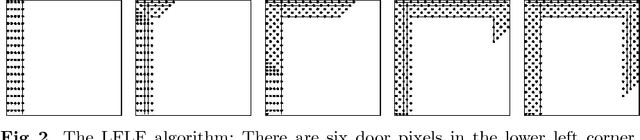
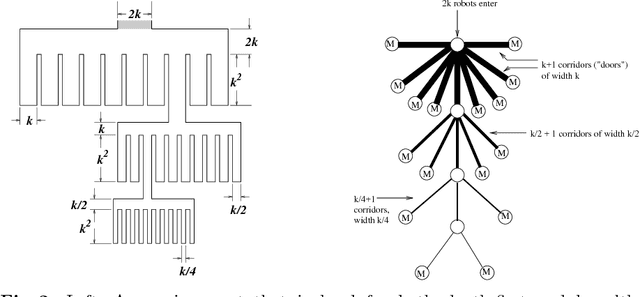
We develop and analyze algorithms for dispersing a swarm of primitive robots in an unknown environment, R. The primary objective is to minimize the makespan, that is, the time to fill the entire region. An environment is composed of pixels that form a connected subset of the integer grid. There is at most one robot per pixel and robots move horizontally or vertically at unit speed. Robots enter R by means of k>=1 door pixels Robots are primitive finite automata, only having local communication, local sensors, and a constant-sized memory. We first give algorithms for the single-door case (i.e., k=1), analyzing the algorithms both theoretically and experimentally. We prove that our algorithms have optimal makespan 2A-1, where A is the area of R. We next give an algorithm for the multi-door case (k>1), based on a wall-following version of the leader-follower strategy. We prove that our strategy is O(log(k+1))-competitive, and that this bound is tight for our strategy and other related strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge