Multi-robot searching with limited sensing range for static and mobile intruders

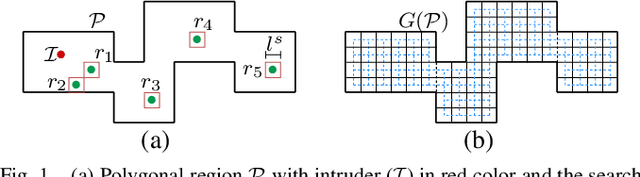
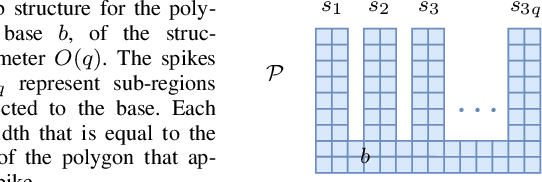
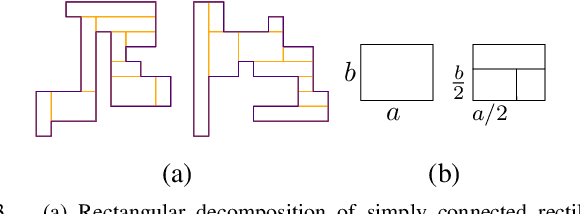
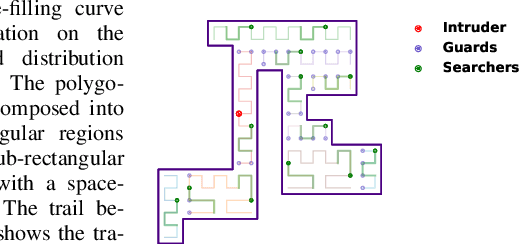
We consider the problem of searching for an intruder in a geometric domain by utilizing multiple search robots. The domain is a simply connected orthogonal polygon with edges parallel to the cartesian coordinate axes. Each robot has a limited sensing capability. We study the problem for both static and mobile intruders. It turns out that the problem of finding an intruder is NP-hard, even for a stationary intruder. Given this intractability, we turn our attention towards developing efficient and robust algorithms, namely methods based on space-filling curves, random search, and cooperative random search. Moreover, for each proposed algorithm, we evaluate the trade-off between the number of search robots and the time required for the robots to complete the search process while considering the geometric properties of the connected orthogonal search area.

Provable Methods for Searching with an Imperfect Sensor

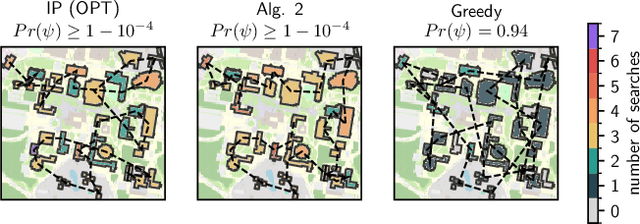
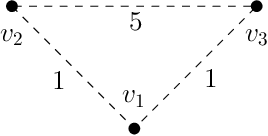
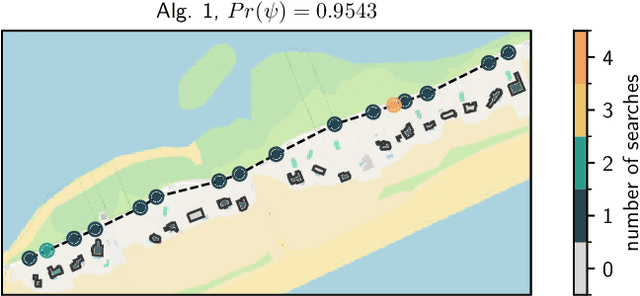
Assume that a target is known to be present at an unknown point among a finite set of locations in the plane. We search for it using a mobile robot that has imperfect sensing capabilities. It takes time for the robot to move between locations and search a location; we have a total time budget within which to conduct the search. We study the problem of computing a search path/strategy for the robot that maximizes the probability of detection of the target. Considering non-uniform travel times between points (e.g., based on the distance between them) is crucial for search and rescue applications; such problems have been investigated to a limited extent due to their inherent complexity. In this paper, we describe fast algorithms with performance guarantees for this search problem and some variants, complement them with complexity results, and perform experiments to observe their performance.

Computing Coordinated Motion Plans for Robot Swarms: The CG:SHOP Challenge 2021

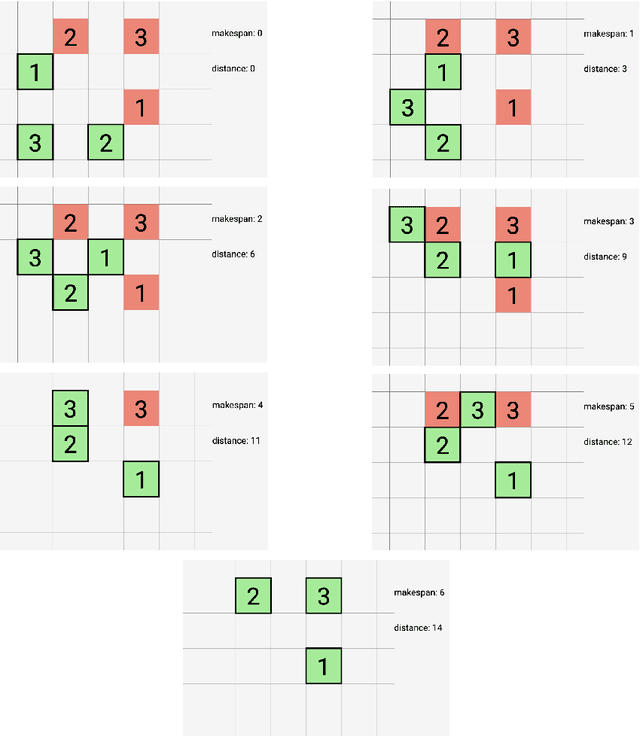
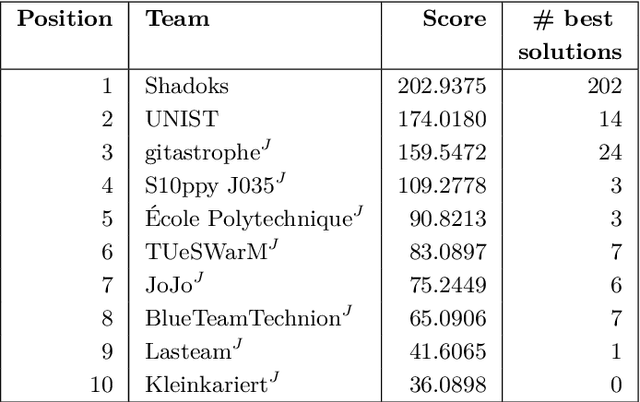
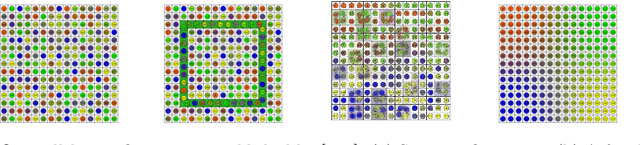
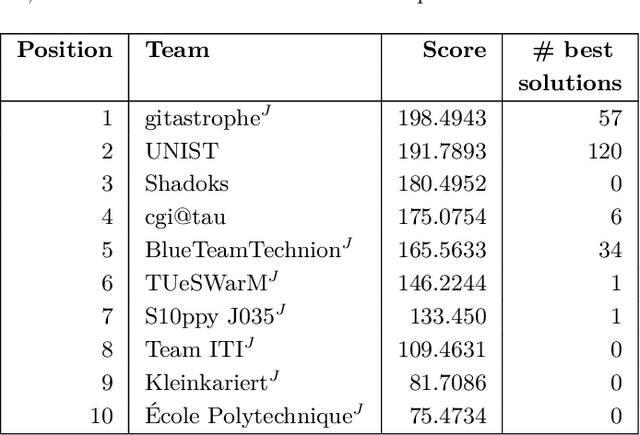
We give an overview of the 2021 Computational Geometry Challenge, which targeted the problem of optimally coordinating a set of robots by computing a family of collision-free trajectories for a set set S of n pixel-shaped objects from a given start configuration into a desired target configuration.

The Snowblower Problem

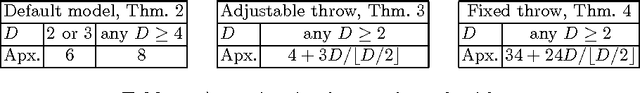
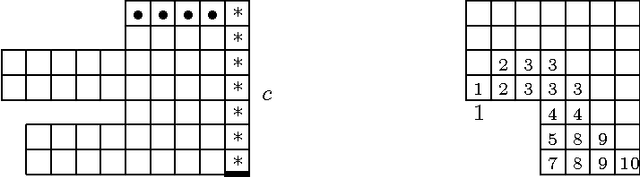
We introduce the snowblower problem (SBP), a new optimization problem that is closely related to milling problems and to some material-handling problems. The objective in the SBP is to compute a short tour for the snowblower to follow to remove all the snow from a domain (driveway, sidewalk, etc.). When a snowblower passes over each region along the tour, it displaces snow into a nearby region. The constraint is that if the snow is piled too high, then the snowblower cannot clear the pile. We give an algorithmic study of the SBP. We show that in general, the problem is NP-complete, and we present polynomial-time approximation algorithms for removing snow under various assumptions about the operation of the snowblower. Most commercially-available snowblowers allow the user to control the direction in which the snow is thrown. We differentiate between the cases in which the snow can be thrown in any direction, in any direction except backwards, and only to the right. For all cases, we give constant-factor approximation algorithms; the constants increase as the throw direction becomes more restricted. Our results are also applicable to robotic vacuuming (or lawnmowing) with bounded capacity dust bin and to some versions of material-handling problems, in which the goal is to rearrange cartons on the floor of a warehouse.

Algorithms for Rapidly Dispersing Robot Swarms in Unknown Environments

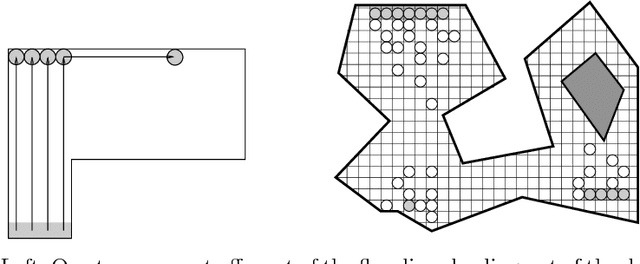
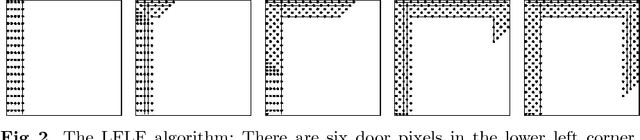
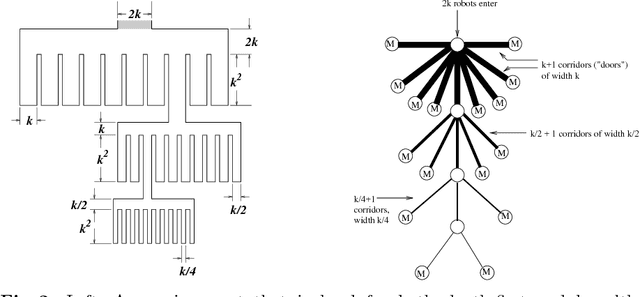
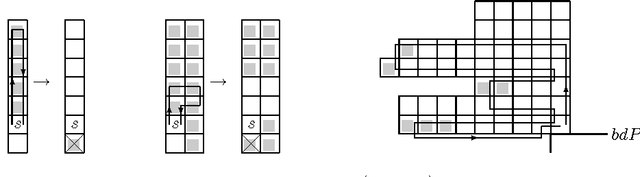
We develop and analyze algorithms for dispersing a swarm of primitive robots in an unknown environment, R. The primary objective is to minimize the makespan, that is, the time to fill the entire region. An environment is composed of pixels that form a connected subset of the integer grid. There is at most one robot per pixel and robots move horizontally or vertically at unit speed. Robots enter R by means of k>=1 door pixels Robots are primitive finite automata, only having local communication, local sensors, and a constant-sized memory. We first give algorithms for the single-door case (i.e., k=1), analyzing the algorithms both theoretically and experimentally. We prove that our algorithms have optimal makespan 2A-1, where A is the area of R. We next give an algorithm for the multi-door case (k>1), based on a wall-following version of the leader-follower strategy. We prove that our strategy is O(log(k+1))-competitive, and that this bound is tight for our strategy and other related strategies.