Multi-Covering a Point Set by $m$ Disks with Minimum Total Area

A common robotics sensing problem is to place sensors to robustly monitor a set of assets, where robustness is assured by requiring asset $p$ to be monitored by at least $\kappa(p)$ sensors. Given $n$ assets that must be observed by $m$ sensors, each with a disk-shaped sensing region, where should the sensors be placed to minimize the total area observed? We provide and analyze a fast heuristic for this problem. We then use the heuristic to initialize an exact Integer Programming solution. Subsequently, we enforce separation constraints between the sensors by modifying the integer program formulation and by changing the disk candidate set.

Provable Methods for Searching with an Imperfect Sensor

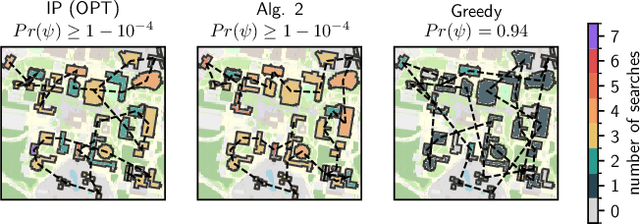
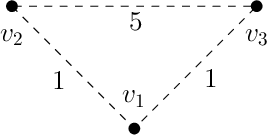
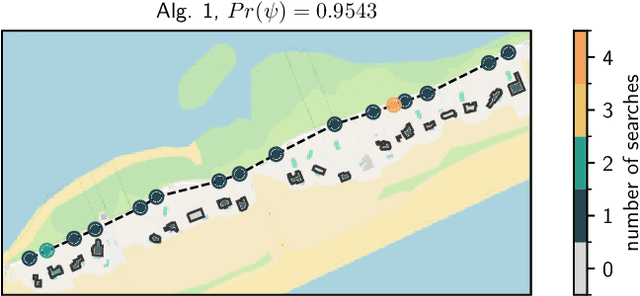
Assume that a target is known to be present at an unknown point among a finite set of locations in the plane. We search for it using a mobile robot that has imperfect sensing capabilities. It takes time for the robot to move between locations and search a location; we have a total time budget within which to conduct the search. We study the problem of computing a search path/strategy for the robot that maximizes the probability of detection of the target. Considering non-uniform travel times between points (e.g., based on the distance between them) is crucial for search and rescue applications; such problems have been investigated to a limited extent due to their inherent complexity. In this paper, we describe fast algorithms with performance guarantees for this search problem and some variants, complement them with complexity results, and perform experiments to observe their performance.