Sándor P. Fekete
Multi-Covering a Point Set by $m$ Disks with Minimum Total Area
Feb 19, 2025Abstract:A common robotics sensing problem is to place sensors to robustly monitor a set of assets, where robustness is assured by requiring asset $p$ to be monitored by at least $\kappa(p)$ sensors. Given $n$ assets that must be observed by $m$ sensors, each with a disk-shaped sensing region, where should the sensors be placed to minimize the total area observed? We provide and analyze a fast heuristic for this problem. We then use the heuristic to initialize an exact Integer Programming solution. Subsequently, we enforce separation constraints between the sensors by modifying the integer program formulation and by changing the disk candidate set.
Moving Matter: Efficient Reconfiguration of Tile Arrangements by a Single Active Robot
Feb 13, 2025
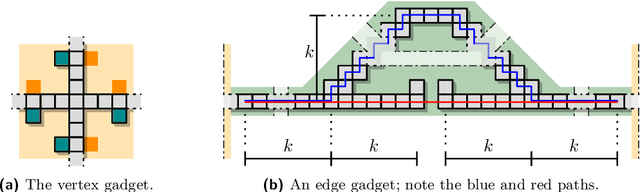
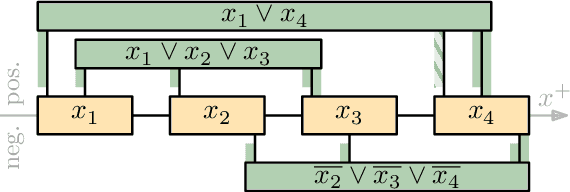
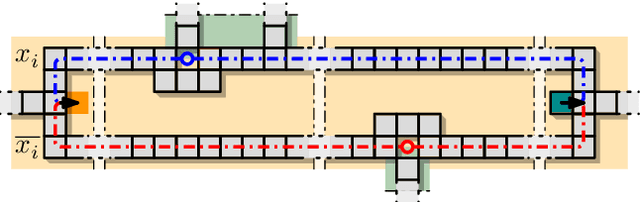
Abstract:We consider the problem of reconfiguring a two-dimensional connected grid arrangement of passive building blocks from a start configuration to a goal configuration, using a single active robot that can move on the tiles, remove individual tiles from a given location and physically move them to a new position by walking on the remaining configuration. The objective is to determine a reconfiguration schedule that minimizes the overall makespan, while ensuring that the tile configuration remains connected. We provide both negative and positive results. (1) We present a generalized version of the problem, parameterized by weighted costs for moving with or without tiles, and show that this is NP-complete. (2) We give a polynomial-time constant-factor approximation algorithm for the case of disjoint start and target bounding boxes. In addition, our approach yields optimal carry distance for 2-scaled instances.
Cooperative 2D Reconfiguration using Spatio-Temporal Planning and Load Transferring
Nov 16, 2022



Abstract:We present progress on the problem of reconfiguring a 2D arrangement of building material by a cooperative set of robots. These robots are subjected to the constraints of avoiding obstacles and maintaining connectivity of the structure. We develop two reconfiguration methods, one based on spatio-temporal planning, and one based on target swapping. Both methods achieve coordinated motion of robots by avoiding deadlocks and maintaining all constraints. Both methods also increase efficiency by reducing the amount of waiting times and lowering combined travel costs. The resulting progress is validated by simulations that also scale the number of robots.
Efficiently Reconfiguring a Connected Swarm of Labeled Robots
Sep 22, 2022

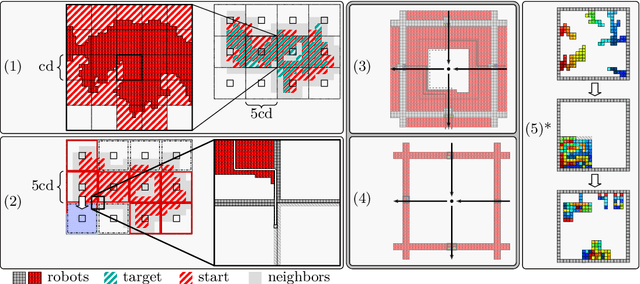
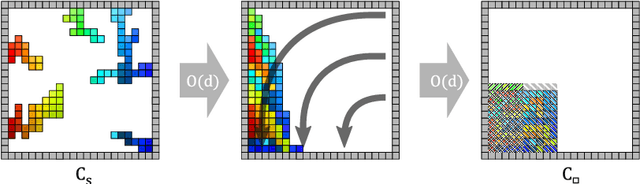
Abstract:When considering motion planning for a swarm of $n$ labeled robots, we need to rearrange a given start configuration into a desired target configuration via a sequence of parallel, continuous, collision-free robot motions. The objective is to reach the new configuration in a minimum amount of time; an important constraint is to keep the swarm connected at all times. Problems of this type have been considered before, with recent notable results achieving constant stretch for not necessarily connected reconfiguration: If mapping the start configuration to the target configuration requires a maximum Manhattan distance of $d$, the total duration of an overall schedule can be bounded to $\mathcal{O}(d)$, which is optimal up to constant factors. However, constant stretch could only be achieved if disconnected reconfiguration is allowed, or for scaled configurations (which arise by increasing all dimensions of a given object by the same multiplicative factor) of unlabeled robots. We resolve these major open problems by (1) establishing a lower bound of $\Omega(\sqrt{n})$ for connected, labeled reconfiguration and, most importantly, by (2) proving that for scaled arrangements, constant stretch for connected reconfiguration can be achieved. In addition, we show that (3) it is NP-hard to decide whether a makespan of 2 can be achieved, while it is possible to check in polynomial time whether a makespan of 1 can be achieved.
Computing Coordinated Motion Plans for Robot Swarms: The CG:SHOP Challenge 2021
Mar 29, 2021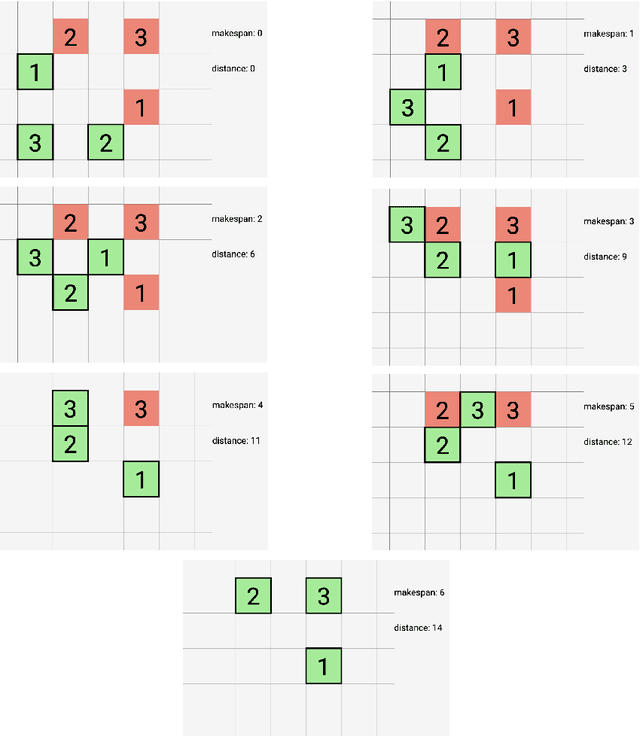
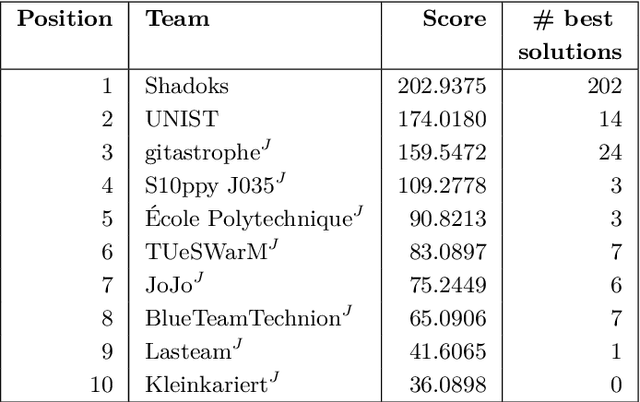
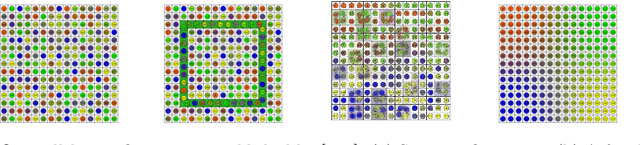
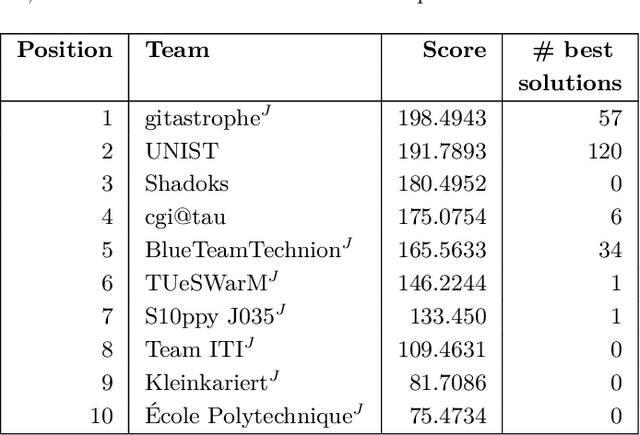
Abstract:We give an overview of the 2021 Computational Geometry Challenge, which targeted the problem of optimally coordinating a set of robots by computing a family of collision-free trajectories for a set set S of n pixel-shaped objects from a given start configuration into a desired target configuration.
Coordinated Motion Planning: Reconfiguring a Swarm of Labeled Robots with Bounded Stretch
Jan 05, 2018
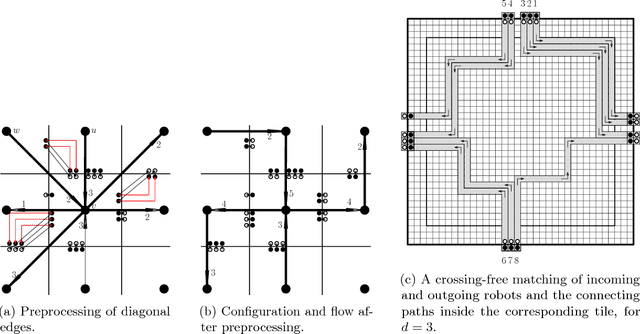
Abstract:We present a number of breakthroughs for coordinated motion planning, in which the objective is to reconfigure a swarm of labeled convex objects by a combination of parallel, continuous, collision-free translations into a given target arrangement. Problems of this type can be traced back to the classic work of Schwartz and Sharir (1983), who gave a method for deciding the existence of a coordinated motion for a set of disks between obstacles; their approach is polynomial in the complexity of the obstacles, but exponential in the number of disks. Other previous work has largely focused on {\em sequential} schedules, in which one robot moves at a time. We provide constant-factor approximation algorithms for minimizing the execution time of a coordinated, {\em parallel} motion plan for a swarm of robots in the absence of obstacles, provided some amount of separability. Our algorithm achieves {\em constant stretch factor}: If all robots are at most $d$ units from their respective starting positions, the total duration of the overall schedule is $O(d)$. Extensions include unlabeled robots and different classes of robots. We also prove that finding a plan with minimal execution time is NP-hard, even for a grid arrangement without any stationary obstacles. On the other hand, we show that for densely packed disks that cannot be well separated, a stretch factor $\Omega(N^{1/4})$ may be required. On the positive side, we establish a stretch factor of $O(N^{1/2})$ even in this case.
Particle Computation: Complexity, Algorithms, and Logic
Dec 04, 2017
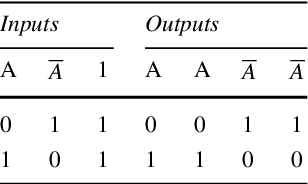


Abstract:We investigate algorithmic control of a large swarm of mobile particles (such as robots, sensors, or building material) that move in a 2D workspace using a global input signal (such as gravity or a magnetic field). We show that a maze of obstacles to the environment can be used to create complex systems. We provide a wide range of results for a wide range of questions. These can be subdivided into external algorithmic problems, in which particle configurations serve as input for computations that are performed elsewhere, and internal logic problems, in which the particle configurations themselves are used for carrying out computations. For external algorithms, we give both negative and positive results. If we are given a set of stationary obstacles, we prove that it is NP-hard to decide whether a given initial configuration of unit-sized particles can be transformed into a desired target configuration. Moreover, we show that finding a control sequence of minimum length is PSPACE-complete. We also work on the inverse problem, providing constructive algorithms to design workspaces that efficiently implement arbitrary permutations between different configurations. For internal logic, we investigate how arbitrary computations can be implemented. We demonstrate how to encode dual-rail logic to build a universal logic gate that concurrently evaluates and, nand, nor, and or operations. Using many of these gates and appropriate interconnects, we can evaluate any logical expression. However, we establish that simulating the full range of complex interactions present in arbitrary digital circuits encounters a fundamental difficulty: a fan-out gate cannot be generated. We resolve this missing component with the help of 2x1 particles, which can create fan-out gates that produce multiple copies of the inputs. Using these gates we provide rules for replicating arbitrary digital circuits.
Collecting a Swarm in a Grid Environment Using Shared, Global Inputs
Jan 02, 2017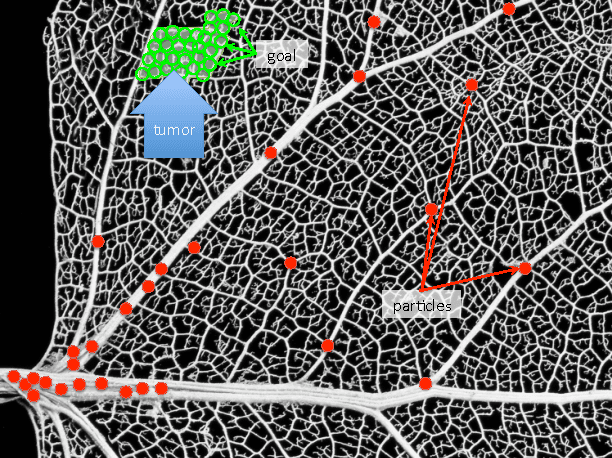
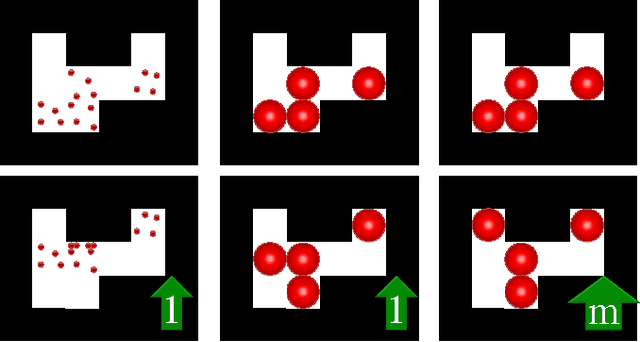

Abstract:This paper investigates efficient techniques to collect and concentrate an under-actuated particle swarm despite obstacles. Concentrating a swarm of particles is of critical importance in health-care for targeted drug delivery, where micro-scale particles must be steered to a goal location. Individual particles must be small in order to navigate through micro-vasculature, but decreasing size brings new challenges. Individual particles are too small to contain on-board power or computation and are instead controlled by a global input, such as an applied fluidic flow or electric field. To make progress, this paper considers a swarm of robots initialized in a grid world in which each position is either free-space or obstacle. This paper provides algorithms that collect all the robots to one position and compares these algorithms on the basis of efficiency and implementation time.
Particle Computation: Designing Worlds to Control Robot Swarms with only Global Signals
Feb 16, 2014
Abstract:Micro- and nanorobots are often controlled by global input signals, such as an electromagnetic or gravitational field. These fields move each robot maximally until it hits a stationary obstacle or another stationary robot. This paper investigates 2D motion-planning complexity for large swarms of simple mobile robots (such as bacteria, sensors, or smart building material). In previous work we proved it is NP-hard to decide whether a given initial configuration can be transformed into a desired target configuration; in this paper we prove a stronger result: the problem of finding an optimal control sequence is PSPACE-complete. On the positive side, we show we can build useful systems by designing obstacles. We present a reconfigurable hardware platform and demonstrate how to form arbitrary permutations and build a compact absolute encoder. We then take the same platform and use dual-rail logic to build a universal logic gate that concurrently evaluates AND, NAND, NOR and OR operations. Using many of these gates and appropriate interconnects we can evaluate any logical expression.
Exploration via Structured Triangulation by a Multi-Robot System with Bearing-Only Low-Resolution Sensors
Feb 03, 2014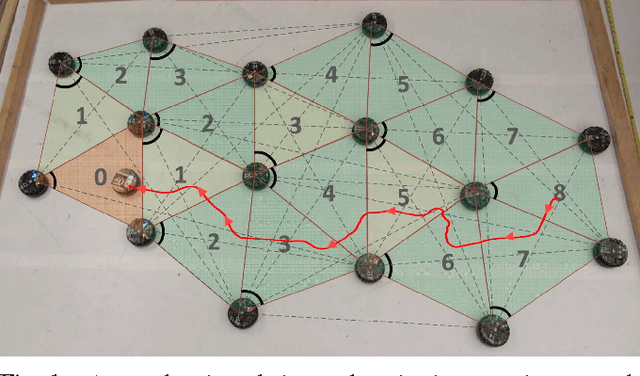
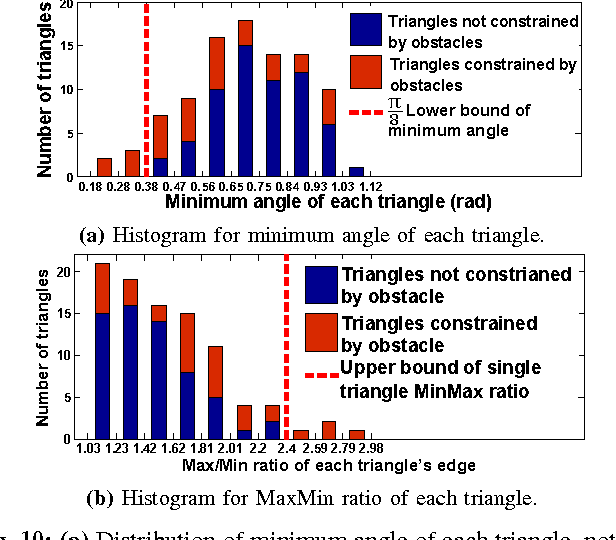
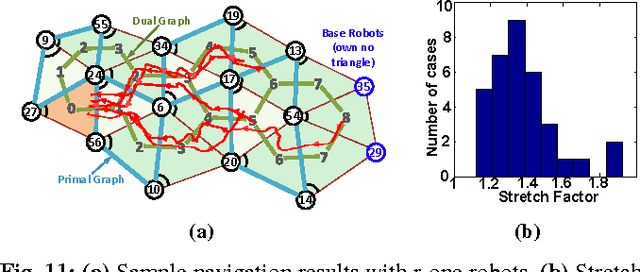
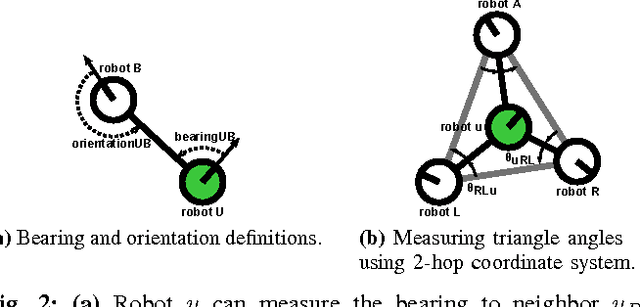
Abstract:This paper presents a distributed approach for exploring and triangulating an unknown region using a multi- robot system. The objective is to produce a covering of an unknown workspace by a fixed number of robots such that the covered region is maximized, solving the Maximum Area Triangulation Problem (MATP). The resulting triangulation is a physical data structure that is a compact representation of the workspace; it contains distributed knowledge of each triangle, adjacent triangles, and the dual graph of the workspace. Algorithms can store information in this physical data structure, such as a routing table for robot navigation Our algorithm builds a triangulation in a closed environment, starting from a single location. It provides coverage with a breadth-first search pattern and completeness guarantees. We show the computational and communication requirements to build and maintain the triangulation and its dual graph are small. Finally, we present a physical navigation algorithm that uses the dual graph, and show that the resulting path lengths are within a constant factor of the shortest-path Euclidean distance. We validate our theoretical results with experiments on triangulating a region with a system of low-cost robots. Analysis of the resulting quality of the triangulation shows that most of the triangles are of high quality, and cover a large area. Implementation of the triangulation, dual graph, and navigation all use communication messages of fixed size, and are a practical solution for large populations of low-cost robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge