Christian Scheffer
Moving Matter: Efficient Reconfiguration of Tile Arrangements by a Single Active Robot
Feb 13, 2025
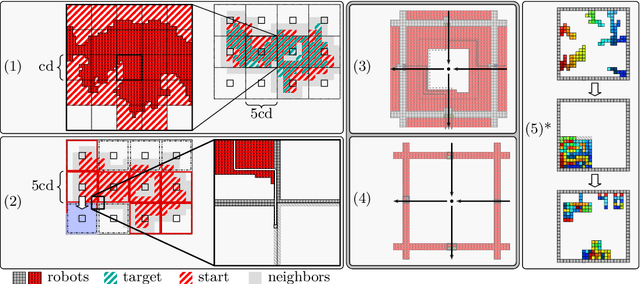
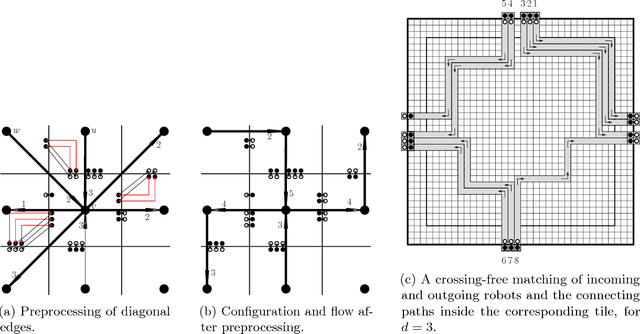
Abstract:We consider the problem of reconfiguring a two-dimensional connected grid arrangement of passive building blocks from a start configuration to a goal configuration, using a single active robot that can move on the tiles, remove individual tiles from a given location and physically move them to a new position by walking on the remaining configuration. The objective is to determine a reconfiguration schedule that minimizes the overall makespan, while ensuring that the tile configuration remains connected. We provide both negative and positive results. (1) We present a generalized version of the problem, parameterized by weighted costs for moving with or without tiles, and show that this is NP-complete. (2) We give a polynomial-time constant-factor approximation algorithm for the case of disjoint start and target bounding boxes. In addition, our approach yields optimal carry distance for 2-scaled instances.
Efficiently Reconfiguring a Connected Swarm of Labeled Robots
Sep 22, 2022

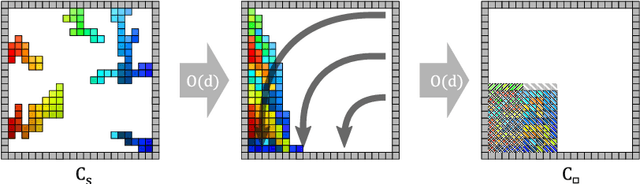
Abstract:When considering motion planning for a swarm of $n$ labeled robots, we need to rearrange a given start configuration into a desired target configuration via a sequence of parallel, continuous, collision-free robot motions. The objective is to reach the new configuration in a minimum amount of time; an important constraint is to keep the swarm connected at all times. Problems of this type have been considered before, with recent notable results achieving constant stretch for not necessarily connected reconfiguration: If mapping the start configuration to the target configuration requires a maximum Manhattan distance of $d$, the total duration of an overall schedule can be bounded to $\mathcal{O}(d)$, which is optimal up to constant factors. However, constant stretch could only be achieved if disconnected reconfiguration is allowed, or for scaled configurations (which arise by increasing all dimensions of a given object by the same multiplicative factor) of unlabeled robots. We resolve these major open problems by (1) establishing a lower bound of $\Omega(\sqrt{n})$ for connected, labeled reconfiguration and, most importantly, by (2) proving that for scaled arrangements, constant stretch for connected reconfiguration can be achieved. In addition, we show that (3) it is NP-hard to decide whether a makespan of 2 can be achieved, while it is possible to check in polynomial time whether a makespan of 1 can be achieved.
Coordinated Motion Planning: Reconfiguring a Swarm of Labeled Robots with Bounded Stretch
Jan 05, 2018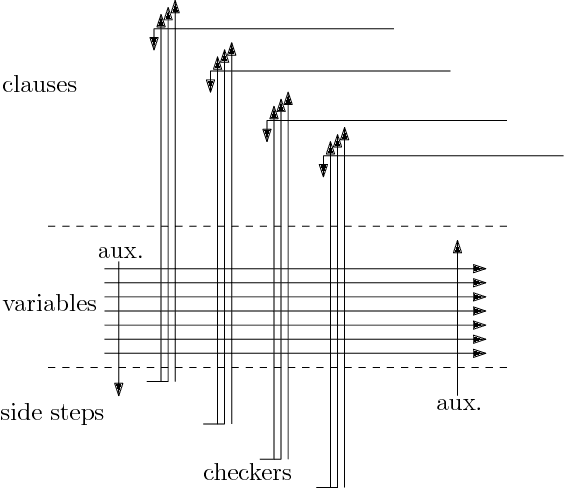
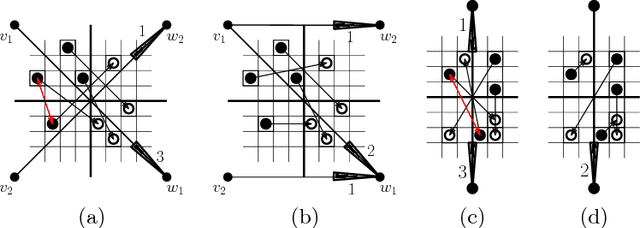
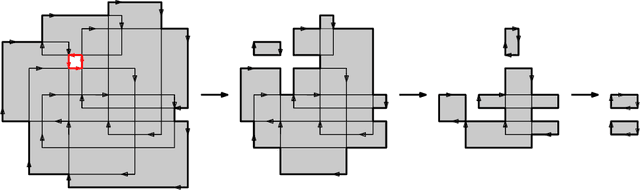
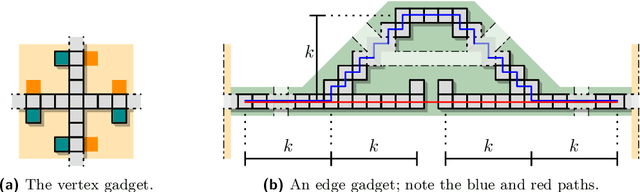
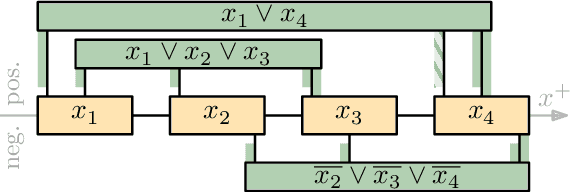
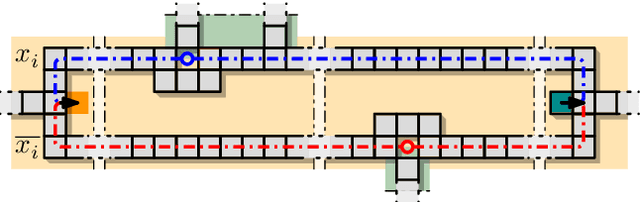
Abstract:We present a number of breakthroughs for coordinated motion planning, in which the objective is to reconfigure a swarm of labeled convex objects by a combination of parallel, continuous, collision-free translations into a given target arrangement. Problems of this type can be traced back to the classic work of Schwartz and Sharir (1983), who gave a method for deciding the existence of a coordinated motion for a set of disks between obstacles; their approach is polynomial in the complexity of the obstacles, but exponential in the number of disks. Other previous work has largely focused on {\em sequential} schedules, in which one robot moves at a time. We provide constant-factor approximation algorithms for minimizing the execution time of a coordinated, {\em parallel} motion plan for a swarm of robots in the absence of obstacles, provided some amount of separability. Our algorithm achieves {\em constant stretch factor}: If all robots are at most $d$ units from their respective starting positions, the total duration of the overall schedule is $O(d)$. Extensions include unlabeled robots and different classes of robots. We also prove that finding a plan with minimal execution time is NP-hard, even for a grid arrangement without any stationary obstacles. On the other hand, we show that for densely packed disks that cannot be well separated, a stretch factor $\Omega(N^{1/4})$ may be required. On the positive side, we establish a stretch factor of $O(N^{1/2})$ even in this case.
Similarity of Polygonal Curves in the Presence of Outliers
Apr 23, 2013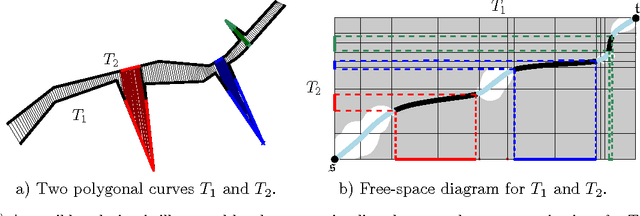
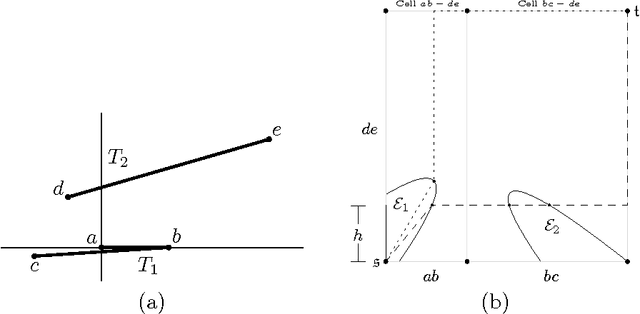
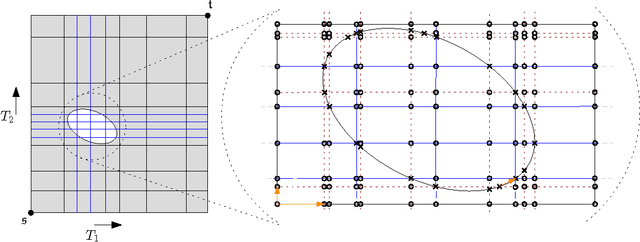
Abstract:The Fr\'{e}chet distance is a well studied and commonly used measure to capture the similarity of polygonal curves. Unfortunately, it exhibits a high sensitivity to the presence of outliers. Since the presence of outliers is a frequently occurring phenomenon in practice, a robust variant of Fr\'{e}chet distance is required which absorbs outliers. We study such a variant here. In this modified variant, our objective is to minimize the length of subcurves of two polygonal curves that need to be ignored (MinEx problem), or alternately, maximize the length of subcurves that are preserved (MaxIn problem), to achieve a given Fr\'{e}chet distance. An exact solution to one problem would imply an exact solution to the other problem. However, we show that these problems are not solvable by radicals over $\mathbb{Q}$ and that the degree of the polynomial equations involved is unbounded in general. This motivates the search for approximate solutions. We present an algorithm, which approximates, for a given input parameter $\delta$, optimal solutions for the \MinEx\ and \MaxIn\ problems up to an additive approximation error $\delta$ times the length of the input curves. The resulting running time is upper bounded by $\mathcal{O} \left(\frac{n^3}{\delta} \log \left(\frac{n}{\delta} \right)\right)$, where $n$ is the complexity of the input polygonal curves.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge