Analysis of Farthest Point Sampling for Approximating Geodesics in a Graph

A standard way to approximate the distance between any two vertices $p$ and $q$ on a mesh is to compute, in the associated graph, a shortest path from $p$ to $q$ that goes through one of $k$ sources, which are well-chosen vertices. Precomputing the distance between each of the $k$ sources to all vertices of the graph yields an efficient computation of approximate distances between any two vertices. One standard method for choosing $k$ sources, which has been used extensively and successfully for isometry-invariant surface processing, is the so-called Farthest Point Sampling (FPS), which starts with a random vertex as the first source, and iteratively selects the farthest vertex from the already selected sources. In this paper, we analyze the stretch factor $\mathcal{F}_{FPS}$ of approximate geodesics computed using FPS, which is the maximum, over all pairs of distinct vertices, of their approximated distance over their geodesic distance in the graph. We show that $\mathcal{F}_{FPS}$ can be bounded in terms of the minimal value $\mathcal{F}^*$ of the stretch factor obtained using an optimal placement of $k$ sources as $\mathcal{F}_{FPS}\leq 2 r_e^2 \mathcal{F}^*+ 2 r_e^2 + 8 r_e + 1$, where $r_e$ is the ratio of the lengths of the longest and the shortest edges of the graph. This provides some evidence explaining why farthest point sampling has been used successfully for isometry-invariant shape processing. Furthermore, we show that it is NP-complete to find $k$ sources that minimize the stretch factor.

Similarity of Polygonal Curves in the Presence of Outliers

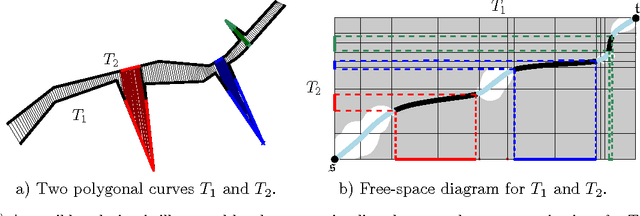
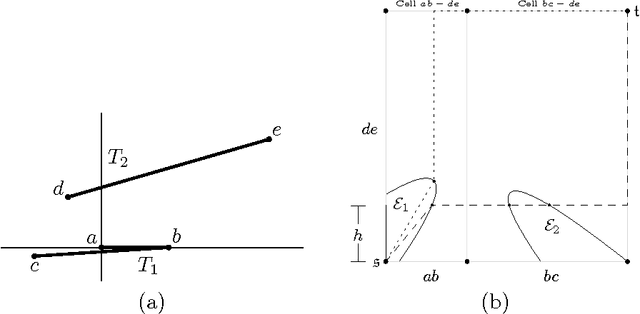
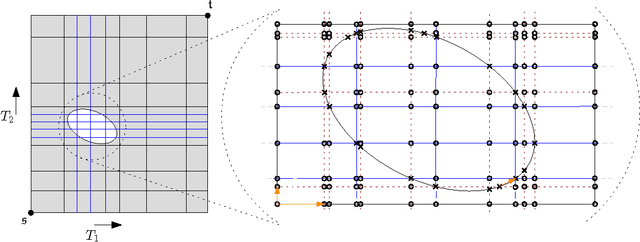
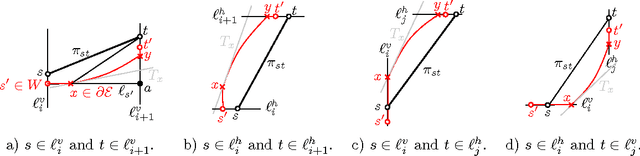
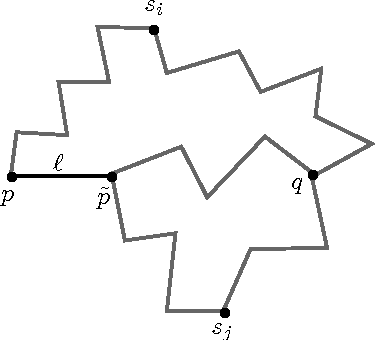
The Fr\'{e}chet distance is a well studied and commonly used measure to capture the similarity of polygonal curves. Unfortunately, it exhibits a high sensitivity to the presence of outliers. Since the presence of outliers is a frequently occurring phenomenon in practice, a robust variant of Fr\'{e}chet distance is required which absorbs outliers. We study such a variant here. In this modified variant, our objective is to minimize the length of subcurves of two polygonal curves that need to be ignored (MinEx problem), or alternately, maximize the length of subcurves that are preserved (MaxIn problem), to achieve a given Fr\'{e}chet distance. An exact solution to one problem would imply an exact solution to the other problem. However, we show that these problems are not solvable by radicals over $\mathbb{Q}$ and that the degree of the polynomial equations involved is unbounded in general. This motivates the search for approximate solutions. We present an algorithm, which approximates, for a given input parameter $\delta$, optimal solutions for the \MinEx\ and \MaxIn\ problems up to an additive approximation error $\delta$ times the length of the input curves. The resulting running time is upper bounded by $\mathcal{O} \left(\frac{n^3}{\delta} \log \left(\frac{n}{\delta} \right)\right)$, where $n$ is the complexity of the input polygonal curves.

An Approximation Algorithm for Computing Shortest Paths in Weighted 3-d Domains

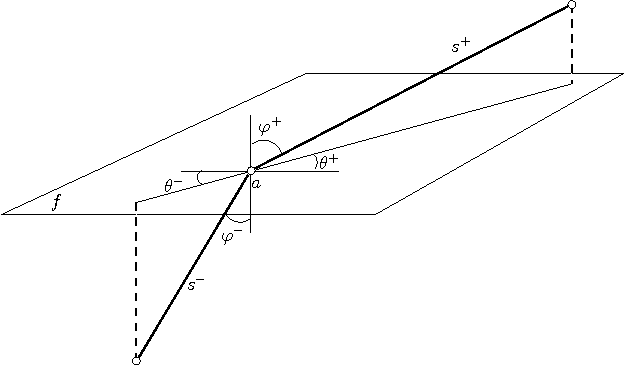
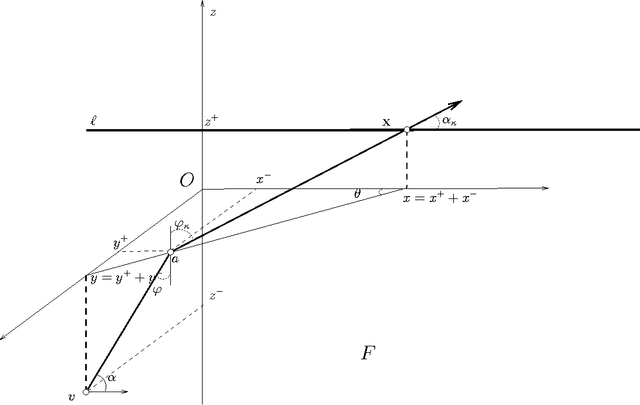
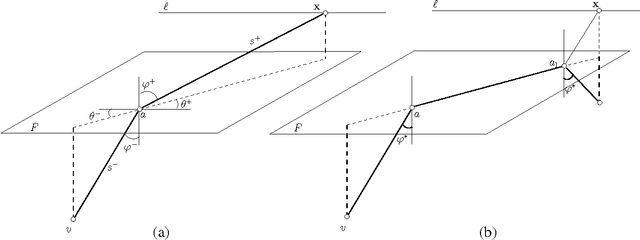
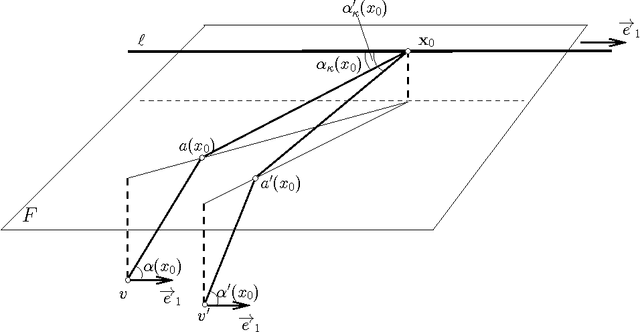
We present the first polynomial time approximation algorithm for computing shortest paths in weighted three-dimensional domains. Given a polyhedral domain $\D$, consisting of $n$ tetrahedra with positive weights, and a real number $\eps\in(0,1)$, our algorithm constructs paths in $\D$ from a fixed source vertex to all vertices of $\D$, whose costs are at most $1+\eps$ times the costs of (weighted) shortest paths, in $O(\C(\D)\frac{n}{\eps^{2.5}}\log\frac{n}{\eps}\log^3\frac{1}{\eps})$ time, where $\C(\D)$ is a geometric parameter related to the aspect ratios of tetrahedra. The efficiency of the proposed algorithm is based on an in-depth study of the local behavior of geodesic paths and additive Voronoi diagrams in weighted three-dimensional domains, which are of independent interest. The paper extends the results of Aleksandrov, Maheshwari and Sack [JACM 2005] to three dimensions.