Sylvain Lazard
Analysis of Farthest Point Sampling for Approximating Geodesics in a Graph
Nov 19, 2013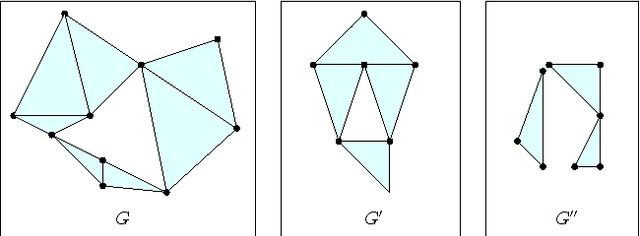
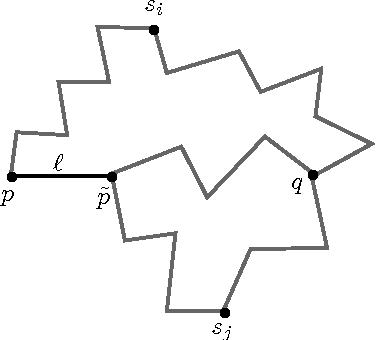
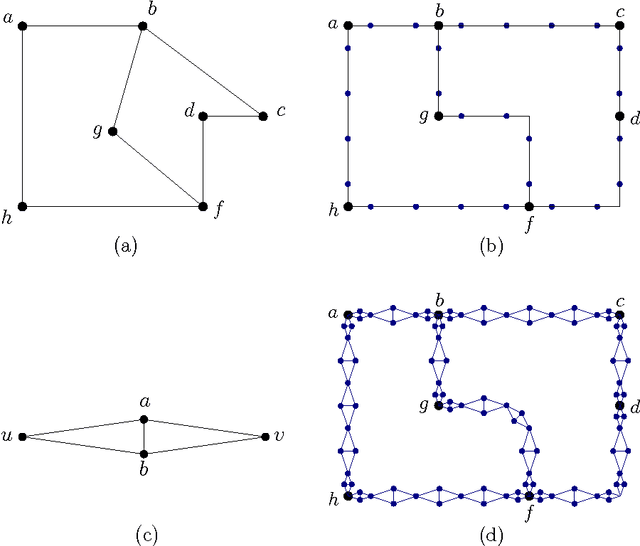

Abstract:A standard way to approximate the distance between any two vertices $p$ and $q$ on a mesh is to compute, in the associated graph, a shortest path from $p$ to $q$ that goes through one of $k$ sources, which are well-chosen vertices. Precomputing the distance between each of the $k$ sources to all vertices of the graph yields an efficient computation of approximate distances between any two vertices. One standard method for choosing $k$ sources, which has been used extensively and successfully for isometry-invariant surface processing, is the so-called Farthest Point Sampling (FPS), which starts with a random vertex as the first source, and iteratively selects the farthest vertex from the already selected sources. In this paper, we analyze the stretch factor $\mathcal{F}_{FPS}$ of approximate geodesics computed using FPS, which is the maximum, over all pairs of distinct vertices, of their approximated distance over their geodesic distance in the graph. We show that $\mathcal{F}_{FPS}$ can be bounded in terms of the minimal value $\mathcal{F}^*$ of the stretch factor obtained using an optimal placement of $k$ sources as $\mathcal{F}_{FPS}\leq 2 r_e^2 \mathcal{F}^*+ 2 r_e^2 + 8 r_e + 1$, where $r_e$ is the ratio of the lengths of the longest and the shortest edges of the graph. This provides some evidence explaining why farthest point sampling has been used successfully for isometry-invariant shape processing. Furthermore, we show that it is NP-complete to find $k$ sources that minimize the stretch factor.
* 13 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge