Pegah Kamousi
A Few-Shot Sequential Approach for Object Counting
Jul 07, 2020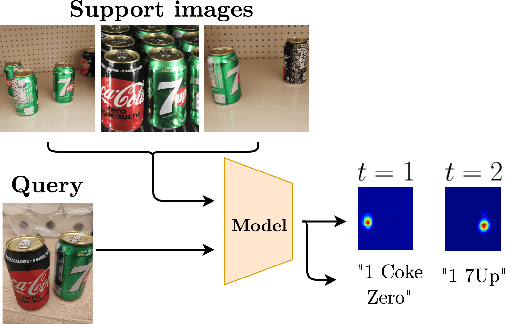
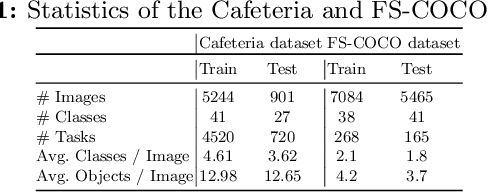
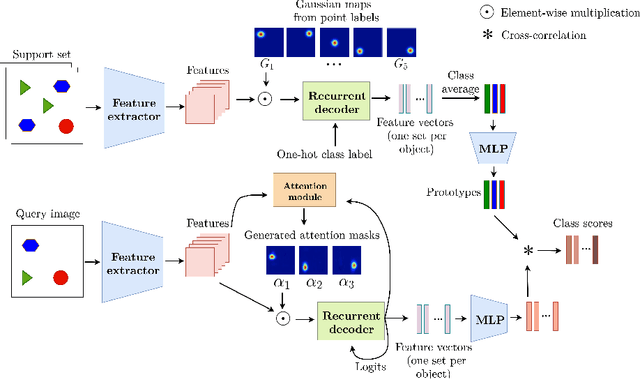
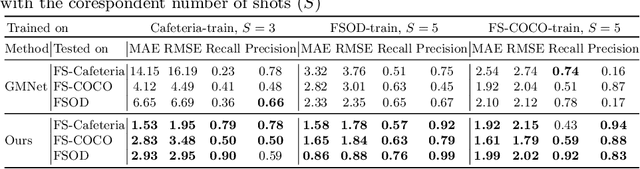
Abstract:In this work, we address the problem of few-shot multi-class object counting with point-level annotations. The proposed technique leverages a class agnostic attention mechanism that sequentially attends to objects in the image and extracts their relevant features. This process is employed on an adapted prototypical-based few-shot approach that uses the extracted features to classify each one either as one of the classes present in the support set images or as background. The proposed technique is trained on point-level annotations and uses a novel loss function that disentangles class-dependent and class-agnostic aspects of the model to help with the task of few-shot object counting. We present our results on a variety of object-counting/detection datasets, including FSOD and MS COCO. In addition, we introduce a new dataset that is specifically designed for weakly supervised multi-class object counting/detection and contains considerably different classes and distribution of number of classes/instances per image compared to the existing datasets. We demonstrate the robustness of our approach by testing our system on a totally different distribution of classes from what it has been trained on.
Analysis of Farthest Point Sampling for Approximating Geodesics in a Graph
Nov 19, 2013
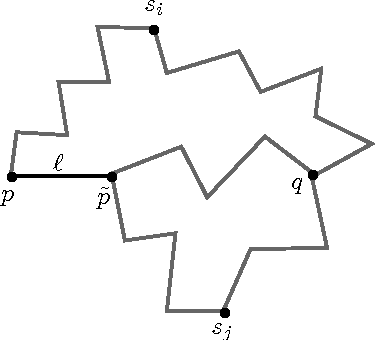

Abstract:A standard way to approximate the distance between any two vertices $p$ and $q$ on a mesh is to compute, in the associated graph, a shortest path from $p$ to $q$ that goes through one of $k$ sources, which are well-chosen vertices. Precomputing the distance between each of the $k$ sources to all vertices of the graph yields an efficient computation of approximate distances between any two vertices. One standard method for choosing $k$ sources, which has been used extensively and successfully for isometry-invariant surface processing, is the so-called Farthest Point Sampling (FPS), which starts with a random vertex as the first source, and iteratively selects the farthest vertex from the already selected sources. In this paper, we analyze the stretch factor $\mathcal{F}_{FPS}$ of approximate geodesics computed using FPS, which is the maximum, over all pairs of distinct vertices, of their approximated distance over their geodesic distance in the graph. We show that $\mathcal{F}_{FPS}$ can be bounded in terms of the minimal value $\mathcal{F}^*$ of the stretch factor obtained using an optimal placement of $k$ sources as $\mathcal{F}_{FPS}\leq 2 r_e^2 \mathcal{F}^*+ 2 r_e^2 + 8 r_e + 1$, where $r_e$ is the ratio of the lengths of the longest and the shortest edges of the graph. This provides some evidence explaining why farthest point sampling has been used successfully for isometry-invariant shape processing. Furthermore, we show that it is NP-complete to find $k$ sources that minimize the stretch factor.
* 13 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge