Melody Construction for Persian lyrics using LSTM recurrent neural networks

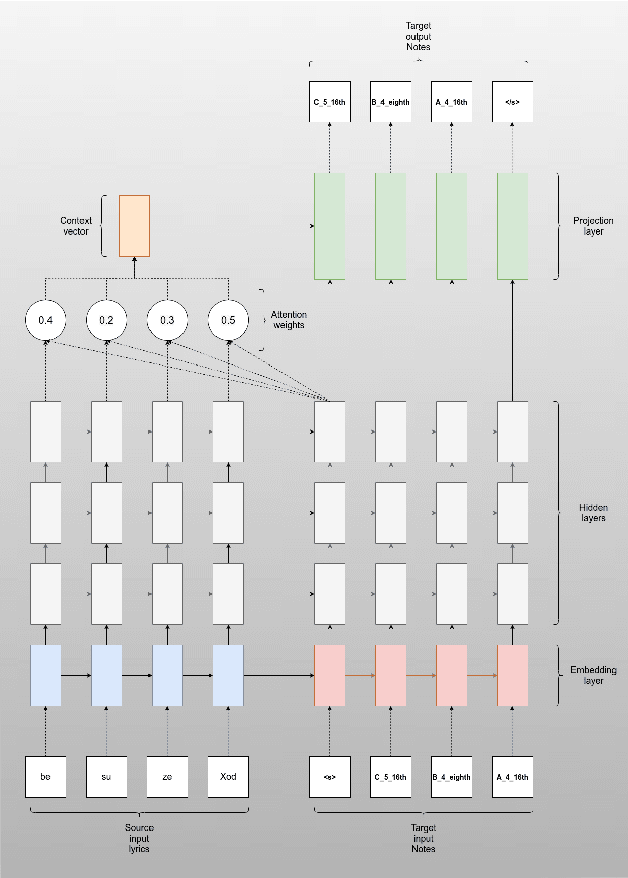
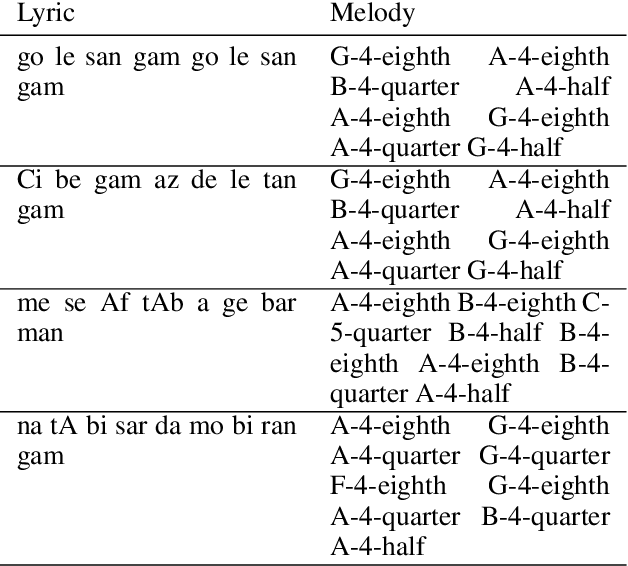
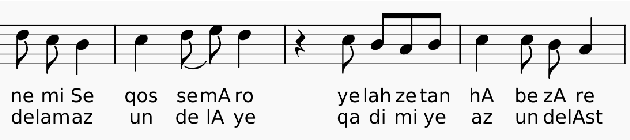
The present paper investigated automatic melody construction for Persian lyrics as an input. It was assumed that there is a phonological correlation between the lyric syllables and the melody in a song. A seq2seq neural network was developed to investigate this assumption, trained on parallel syllable and note sequences in Persian songs to suggest a pleasant melody for a new sequence of syllables. More than 100 pieces of Persian music were collected and converted from the printed version to the digital format due to the lack of a dataset on Persian digital music. Finally, 14 new lyrics were given to the model as input, and the suggested melodies were performed and recorded by music experts to evaluate the trained model. The evaluation was conducted using an audio questionnaire, which more than 170 persons answered. According to the answers about the pleasantness of melody, the system outputs scored an average of 3.005 from 5, while the human-made melodies for the same lyrics obtained an average score of 4.078.

Vocal Melody Construction for Persian Lyrics Using LSTM Recurrent Neural Networks

The present paper investigated automatic melody construction for Persian lyrics as an input. It was assumed that there is a phonological correlation between the lyric syllables and the melody in a song. A seq2seq neural network was developed to investigate this assumption, trained on parallel syllable and note sequences in Persian songs to suggest a pleasant melody for a new sequence of syllables. More than 100 pieces of Persian music were collected and converted from the printed version to the digital format due to the lack of a dataset on Persian digital music. Finally, 14 new lyrics were given to the model as input, and the suggested melodies were performed and recorded by music experts to evaluate the trained model. The evaluation was conducted using an audio questionnaire, which more than 170 persons answered. According to the answers about the pleasantness of melody, the system outputs scored an average of 3.005 from 5, while the human-made melodies for the same lyrics obtained an average score of 4.078.

Reduced Jeffries-Matusita distance: A Novel Loss Function to Improve Generalization Performance of Deep Classification Models

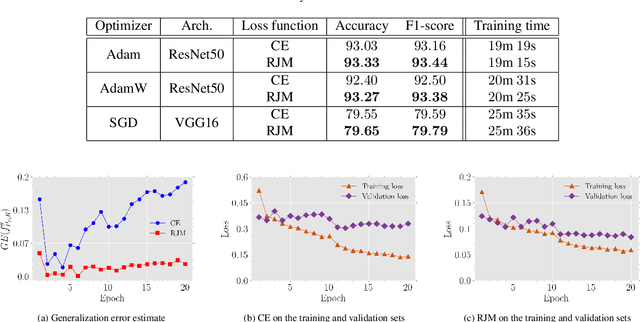
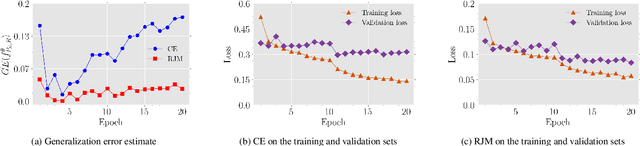
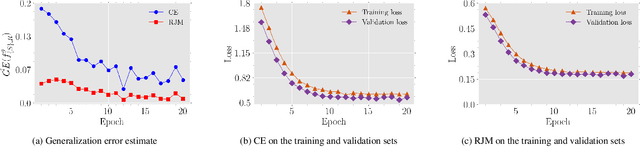
The generalization performance of deep neural networks in classification tasks is a major concern in machine learning research. Despite widespread techniques used to diminish the over-fitting issue such as data augmentation, pseudo-labeling, regularization, and ensemble learning, this performance still needs to be enhanced with other approaches. In recent years, it has been theoretically demonstrated that the loss function characteristics i.e. its Lipschitzness and maximum value affect the generalization performance of deep neural networks which can be utilized as a guidance to propose novel distance measures. In this paper, by analyzing the aforementioned characteristics, we introduce a distance called Reduced Jeffries-Matusita as a loss function for training deep classification models to reduce the over-fitting issue. In our experiments, we evaluate the new loss function in two different problems: image classification in computer vision and node classification in the context of graph learning. The results show that the new distance measure stabilizes the training process significantly, enhances the generalization ability, and improves the performance of the models in the Accuracy and F1-score metrics, even if the training set size is small.

Lipschitzness Effect of a Loss Function on Generalization Performance of Deep Neural Networks Trained by Adam and AdamW Optimizers

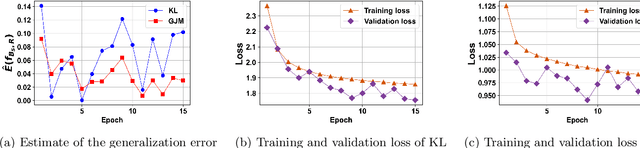
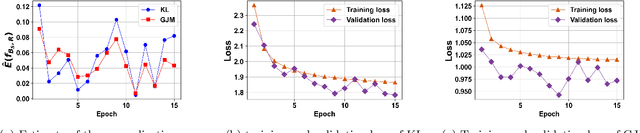
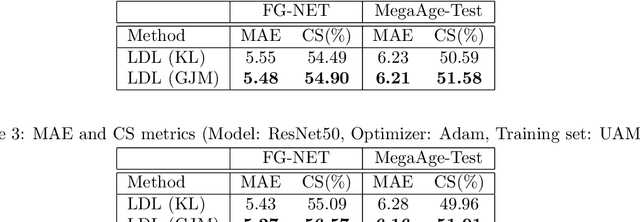
The generalization performance of deep neural networks with regard to the optimization algorithm is one of the major concerns in machine learning. This performance can be affected by various factors. In this paper, we theoretically prove that the Lipschitz constant of a loss function is an important factor to diminish the generalization error of the output model obtained by Adam or AdamW. The results can be used as a guideline for choosing the loss function when the optimization algorithm is Adam or AdamW. In addition, to evaluate the theoretical bound in a practical setting, we choose the human age estimation problem in computer vision. For assessing the generalization better, the training and test datasets are drawn from different distributions. Our experimental evaluation shows that the loss function with lower Lipschitz constant and maximum value improves the generalization of the model trained by Adam or AdamW.

PREDICT: Persian Reverse Dictionary

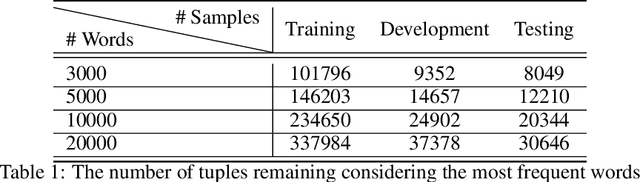
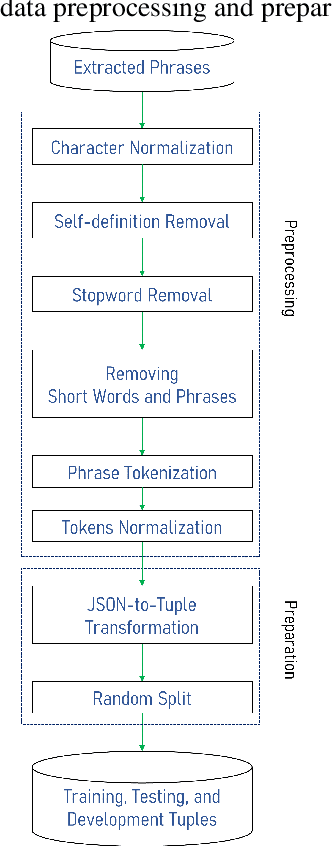
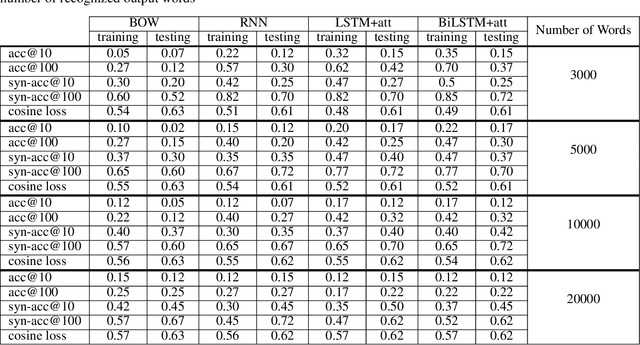
Finding the appropriate words to convey concepts (i.e., lexical access) is essential for effective communication. Reverse dictionaries fulfill this need by helping individuals to find the word(s) which could relate to a specific concept or idea. To the best of our knowledge, this resource has not been available for the Persian language. In this paper, we compare four different architectures for implementing a Persian reverse dictionary (PREDICT). We evaluate our models using (phrase,word) tuples extracted from the only Persian dictionaries available online, namely Amid, Moein, and Dehkhoda where the phrase describes the word. Given the phrase, a model suggests the most relevant word(s) in terms of the ability to convey the concept. The model is considered to perform well if the correct word is one of its top suggestions. Our experiments show that a model consisting of Long Short-Term Memory (LSTM) units enhanced by an additive attention mechanism is enough to produce suggestions comparable to (or in some cases better than) the word in the original dictionary. The study also reveals that the model sometimes produces the synonyms of the word as its output which led us to introduce a new metric for the evaluation of reverse dictionaries called Synonym Accuracy accounting for the percentage of times the event of producing the word or a synonym of it occurs. The assessment of the best model using this new metric also indicates that at least 62% of the times, it produces an accurate result within the top 100 suggestions.

Similarity of Polygonal Curves in the Presence of Outliers

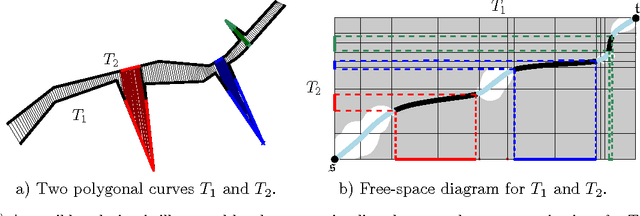
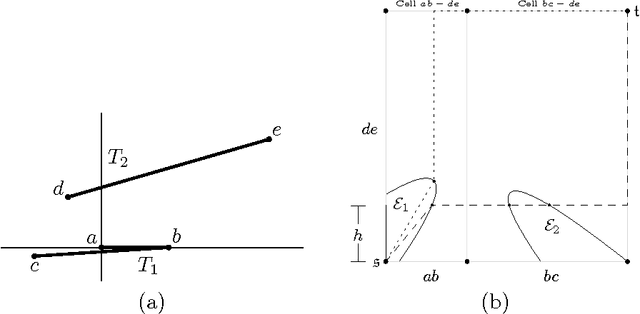
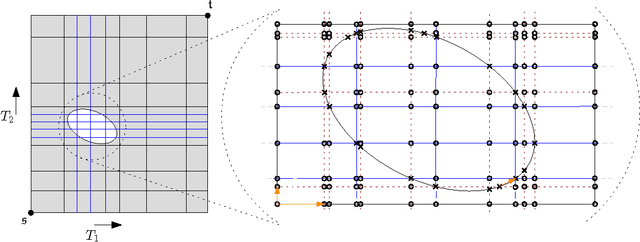
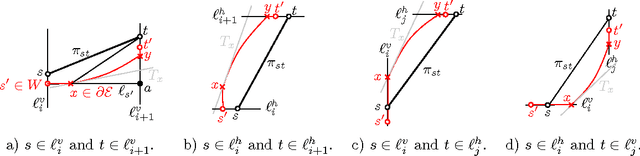
The Fr\'{e}chet distance is a well studied and commonly used measure to capture the similarity of polygonal curves. Unfortunately, it exhibits a high sensitivity to the presence of outliers. Since the presence of outliers is a frequently occurring phenomenon in practice, a robust variant of Fr\'{e}chet distance is required which absorbs outliers. We study such a variant here. In this modified variant, our objective is to minimize the length of subcurves of two polygonal curves that need to be ignored (MinEx problem), or alternately, maximize the length of subcurves that are preserved (MaxIn problem), to achieve a given Fr\'{e}chet distance. An exact solution to one problem would imply an exact solution to the other problem. However, we show that these problems are not solvable by radicals over $\mathbb{Q}$ and that the degree of the polynomial equations involved is unbounded in general. This motivates the search for approximate solutions. We present an algorithm, which approximates, for a given input parameter $\delta$, optimal solutions for the \MinEx\ and \MaxIn\ problems up to an additive approximation error $\delta$ times the length of the input curves. The resulting running time is upper bounded by $\mathcal{O} \left(\frac{n^3}{\delta} \log \left(\frac{n}{\delta} \right)\right)$, where $n$ is the complexity of the input polygonal curves.