Reduced Jeffries-Matusita distance: A Novel Loss Function to Improve Generalization Performance of Deep Classification Models

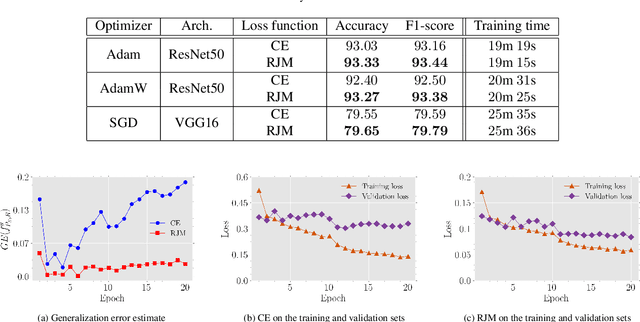
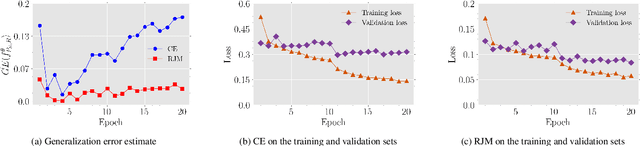
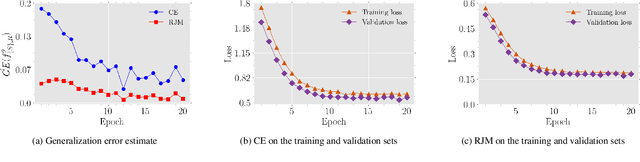
The generalization performance of deep neural networks in classification tasks is a major concern in machine learning research. Despite widespread techniques used to diminish the over-fitting issue such as data augmentation, pseudo-labeling, regularization, and ensemble learning, this performance still needs to be enhanced with other approaches. In recent years, it has been theoretically demonstrated that the loss function characteristics i.e. its Lipschitzness and maximum value affect the generalization performance of deep neural networks which can be utilized as a guidance to propose novel distance measures. In this paper, by analyzing the aforementioned characteristics, we introduce a distance called Reduced Jeffries-Matusita as a loss function for training deep classification models to reduce the over-fitting issue. In our experiments, we evaluate the new loss function in two different problems: image classification in computer vision and node classification in the context of graph learning. The results show that the new distance measure stabilizes the training process significantly, enhances the generalization ability, and improves the performance of the models in the Accuracy and F1-score metrics, even if the training set size is small.

Lipschitzness Effect of a Loss Function on Generalization Performance of Deep Neural Networks Trained by Adam and AdamW Optimizers

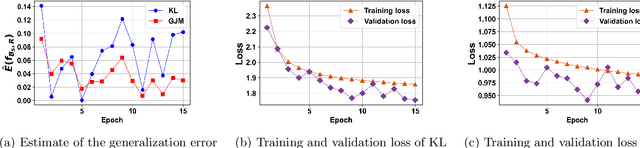
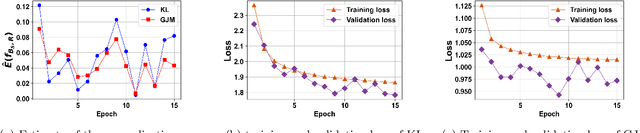
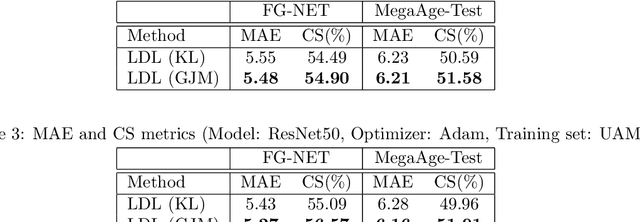
The generalization performance of deep neural networks with regard to the optimization algorithm is one of the major concerns in machine learning. This performance can be affected by various factors. In this paper, we theoretically prove that the Lipschitz constant of a loss function is an important factor to diminish the generalization error of the output model obtained by Adam or AdamW. The results can be used as a guideline for choosing the loss function when the optimization algorithm is Adam or AdamW. In addition, to evaluate the theoretical bound in a practical setting, we choose the human age estimation problem in computer vision. For assessing the generalization better, the training and test datasets are drawn from different distributions. Our experimental evaluation shows that the loss function with lower Lipschitz constant and maximum value improves the generalization of the model trained by Adam or AdamW.