Jörg-Rüdiger Sack
Predicting the Citation Count and CiteScore of Journals One Year in Advance
Oct 24, 2022Abstract:Prediction of the future performance of academic journals is a task that can benefit a variety of stakeholders including editorial staff, publishers, indexing services, researchers, university administrators and granting agencies. Using historical data on journal performance, this can be framed as a machine learning regression problem. In this work, we study two such regression tasks: 1) prediction of the number of citations a journal will receive during the next calendar year, and 2) prediction of the Elsevier CiteScore a journal will be assigned for the next calendar year. To address these tasks, we first create a dataset of historical bibliometric data for journals indexed in Scopus. We propose the use of neural network models trained on our dataset to predict the future performance of journals. To this end, we perform feature selection and model configuration for a Multi-Layer Perceptron and a Long Short-Term Memory. Through experimental comparisons to heuristic prediction baselines and classical machine learning models, we demonstrate superior performance in our proposed models for the prediction of future citation and CiteScore values.
Similarity of Polygonal Curves in the Presence of Outliers
Apr 23, 2013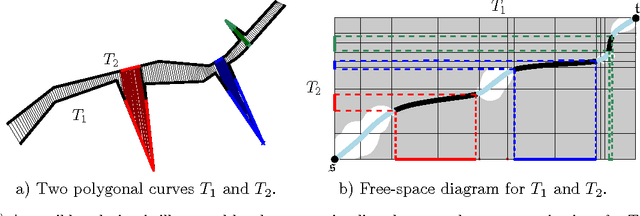
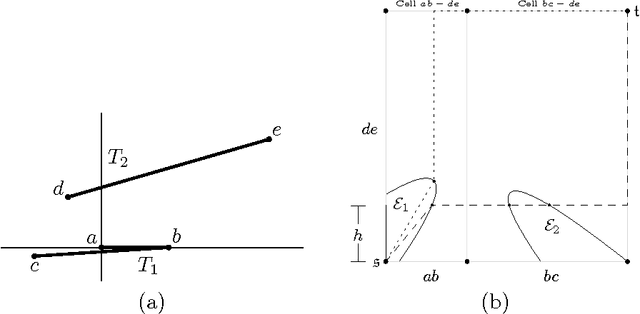
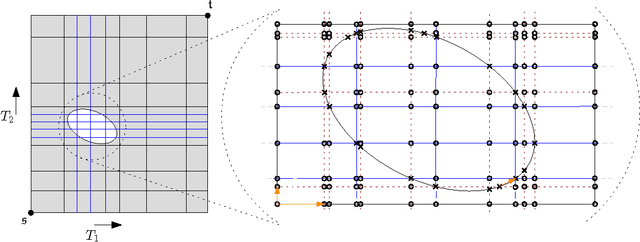
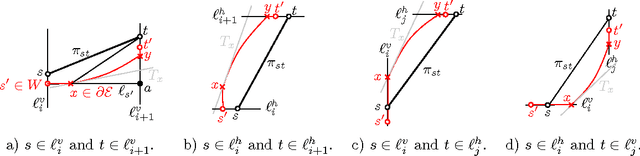
Abstract:The Fr\'{e}chet distance is a well studied and commonly used measure to capture the similarity of polygonal curves. Unfortunately, it exhibits a high sensitivity to the presence of outliers. Since the presence of outliers is a frequently occurring phenomenon in practice, a robust variant of Fr\'{e}chet distance is required which absorbs outliers. We study such a variant here. In this modified variant, our objective is to minimize the length of subcurves of two polygonal curves that need to be ignored (MinEx problem), or alternately, maximize the length of subcurves that are preserved (MaxIn problem), to achieve a given Fr\'{e}chet distance. An exact solution to one problem would imply an exact solution to the other problem. However, we show that these problems are not solvable by radicals over $\mathbb{Q}$ and that the degree of the polynomial equations involved is unbounded in general. This motivates the search for approximate solutions. We present an algorithm, which approximates, for a given input parameter $\delta$, optimal solutions for the \MinEx\ and \MaxIn\ problems up to an additive approximation error $\delta$ times the length of the input curves. The resulting running time is upper bounded by $\mathcal{O} \left(\frac{n^3}{\delta} \log \left(\frac{n}{\delta} \right)\right)$, where $n$ is the complexity of the input polygonal curves.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge