Decoy Selection for Protein Structure Prediction Via Extreme Gradient Boosting and Ranking

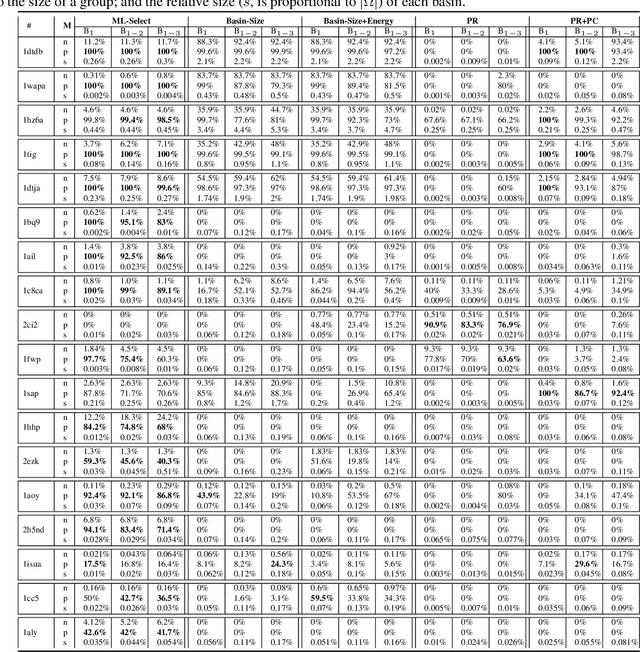
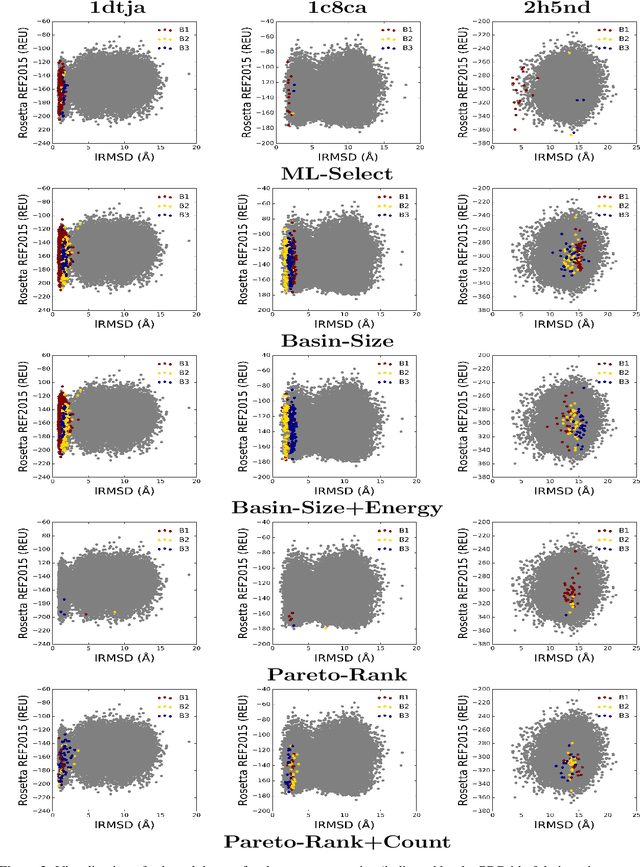
Identifying one or more biologically-active/native decoys from millions of non-native decoys is one of the major challenges in computational structural biology. The extreme lack of balance in positive and negative samples (native and non-native decoys) in a decoy set makes the problem even more complicated. Consensus methods show varied success in handling the challenge of decoy selection despite some issues associated with clustering large decoy sets and decoy sets that do not show much structural similarity. Recent investigations into energy landscape-based decoy selection approaches show promises. However, lack of generalization over varied test cases remains a bottleneck for these methods. We propose a novel decoy selection method, ML-Select, a machine learning framework that exploits the energy landscape associated with the structure space probed through a template-free decoy generation. The proposed method outperforms both clustering and energy ranking-based methods, all the while consistently offering better performance on varied test-cases. Moreover, ML-Select shows promising results even for the decoy sets consisting of mostly low-quality decoys. ML-Select is a useful method for decoy selection. This work suggests further research in finding more effective ways to adopt machine learning frameworks in achieving robust performance for decoy selection in template-free protein structure prediction.

An Approximation Algorithm for Computing Shortest Paths in Weighted 3-d Domains

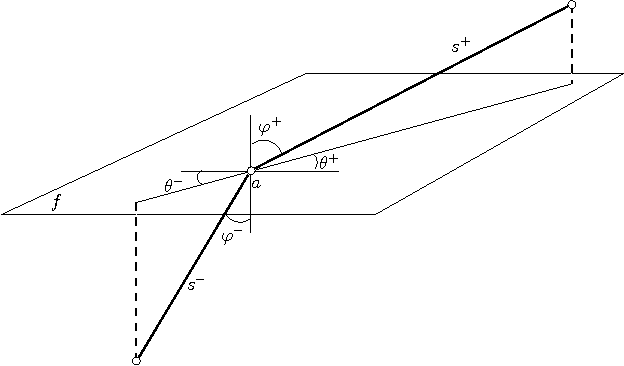
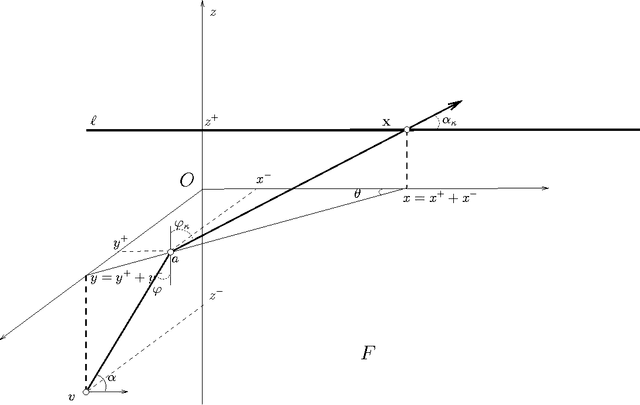
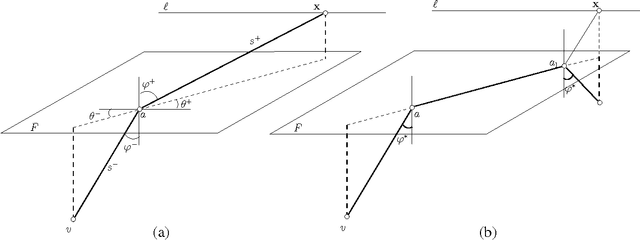
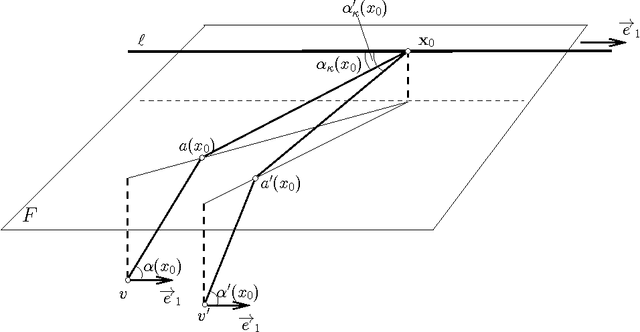
We present the first polynomial time approximation algorithm for computing shortest paths in weighted three-dimensional domains. Given a polyhedral domain $\D$, consisting of $n$ tetrahedra with positive weights, and a real number $\eps\in(0,1)$, our algorithm constructs paths in $\D$ from a fixed source vertex to all vertices of $\D$, whose costs are at most $1+\eps$ times the costs of (weighted) shortest paths, in $O(\C(\D)\frac{n}{\eps^{2.5}}\log\frac{n}{\eps}\log^3\frac{1}{\eps})$ time, where $\C(\D)$ is a geometric parameter related to the aspect ratios of tetrahedra. The efficiency of the proposed algorithm is based on an in-depth study of the local behavior of geodesic paths and additive Voronoi diagrams in weighted three-dimensional domains, which are of independent interest. The paper extends the results of Aleksandrov, Maheshwari and Sack [JACM 2005] to three dimensions.