Estimating Spatially-Dependent GPS Errors Using a Swarm of Robots

External factors, including urban canyons and adversarial interference, can lead to Global Positioning System (GPS) inaccuracies that vary as a function of the position in the environment. This study addresses the challenge of estimating a static, spatially-varying error function using a team of robots. We introduce a State Bias Estimation Algorithm (SBE) whose purpose is to estimate the GPS biases. The central idea is to use sensed estimates of the range and bearing to the other robots in the team to estimate changes in bias across the environment. A set of drones moves in a 2D environment, each sampling data from GPS, range, and bearing sensors. The biases calculated by the SBE at estimated positions are used to train a Gaussian Process Regression (GPR) model. We use a Sparse Gaussian process-based Informative Path Planning (IPP) algorithm that identifies high-value regions of the environment for data collection. The swarm plans paths that maximize information gain in each iteration, further refining their understanding of the environment's positional bias landscape. We evaluated SBE and IPP in simulation and compared the IPP methodology to an open-loop strategy.

Multi-Covering a Point Set by $m$ Disks with Minimum Total Area

A common robotics sensing problem is to place sensors to robustly monitor a set of assets, where robustness is assured by requiring asset $p$ to be monitored by at least $\kappa(p)$ sensors. Given $n$ assets that must be observed by $m$ sensors, each with a disk-shaped sensing region, where should the sensors be placed to minimize the total area observed? We provide and analyze a fast heuristic for this problem. We then use the heuristic to initialize an exact Integer Programming solution. Subsequently, we enforce separation constraints between the sensors by modifying the integer program formulation and by changing the disk candidate set.

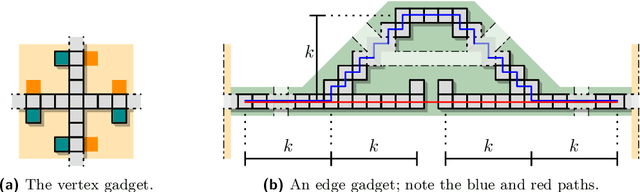
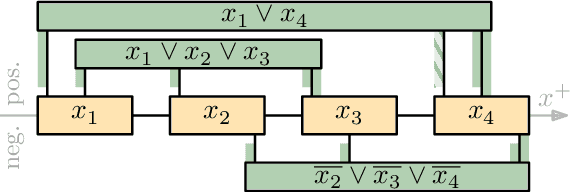
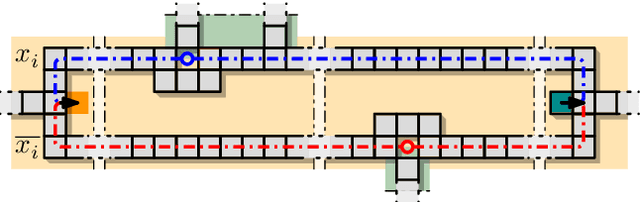
Moving Matter: Efficient Reconfiguration of Tile Arrangements by a Single Active Robot

We consider the problem of reconfiguring a two-dimensional connected grid arrangement of passive building blocks from a start configuration to a goal configuration, using a single active robot that can move on the tiles, remove individual tiles from a given location and physically move them to a new position by walking on the remaining configuration. The objective is to determine a reconfiguration schedule that minimizes the overall makespan, while ensuring that the tile configuration remains connected. We provide both negative and positive results. (1) We present a generalized version of the problem, parameterized by weighted costs for moving with or without tiles, and show that this is NP-complete. (2) We give a polynomial-time constant-factor approximation algorithm for the case of disjoint start and target bounding boxes. In addition, our approach yields optimal carry distance for 2-scaled instances.

An Analytic Solution to the 3D CSC Dubins Path Problem

We present an analytic solution to the 3D Dubins path problem for paths composed of an initial circular arc, a straight component, and a final circular arc. These are commonly called CSC paths. By modeling the start and goal configurations of the path as the base frame and final frame of an RRPRR manipulator, we treat this as an inverse kinematics problem. The kinematic features of the 3D Dubins path are built into the constraints of our manipulator model. Furthermore, we show that the number of solutions is not constant, with up to seven valid CSC path solutions even in non-singular regions. An implementation of solution is available at https://github.com/aabecker/dubins3D.

Minimum-Time Planar Paths with up to Two Constant Acceleration Inputs and $L_2$ Velocity and Acceleration Constraints

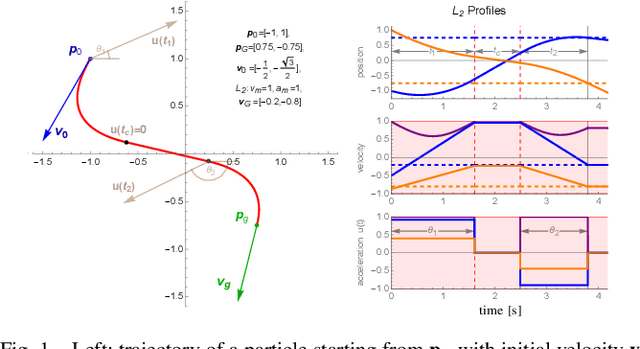
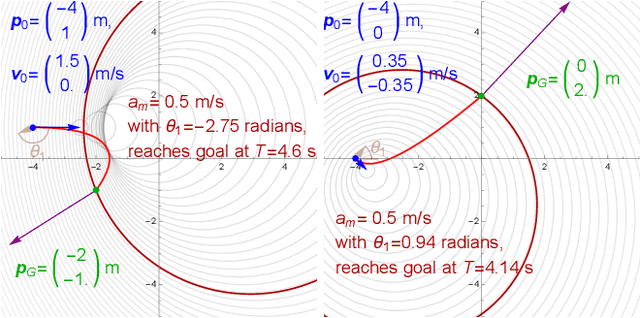
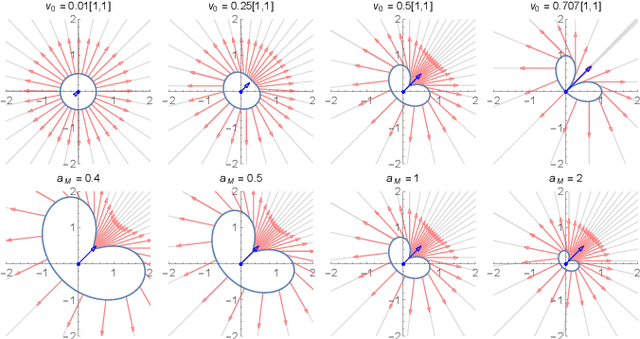
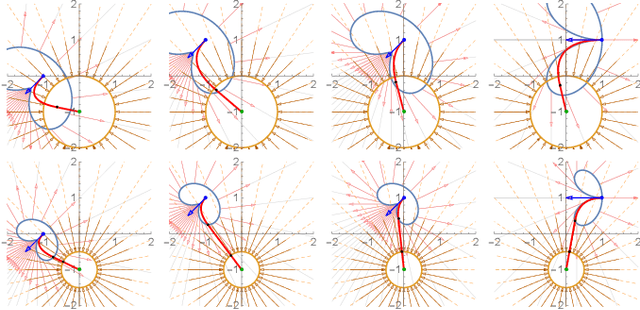
Given starting and ending positions and velocities, $L_2$ bounds on the acceleration and velocity, and the restriction to no more than two constant control inputs, this paper provides routines to compute the minimal-time path. Closed form solutions are provided for reaching a position in minimum time with and without a velocity bound, and for stopping at the goal position. A numeric solver is used to reach a goal position and velocity with no more than two constant control inputs. If a cruising phase at the terminal velocity is needed, this requires solving a non-linear equation with a single parameter. Code is provided on GitHub at https://github.com/RoboticSwarmControl/MinTimeL2pathsConstraints.

Computing Motion Plans for Assembling Particles with Global Control

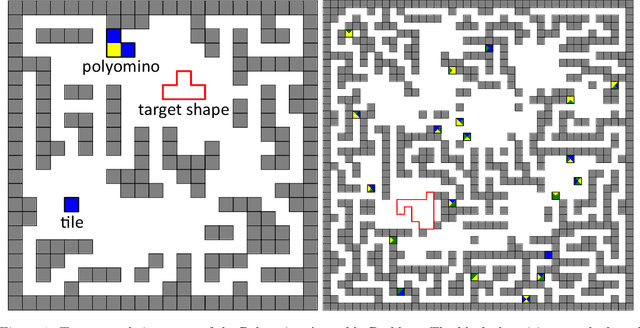
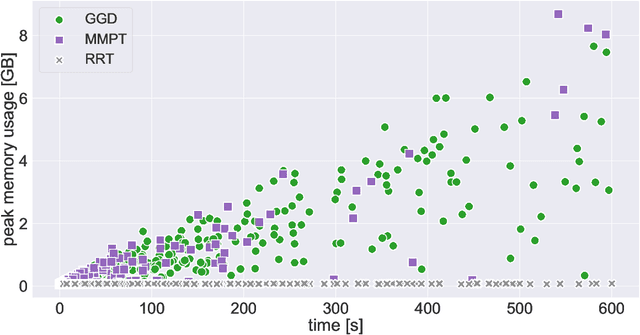
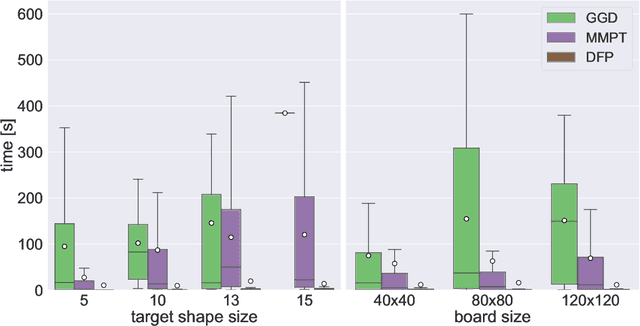
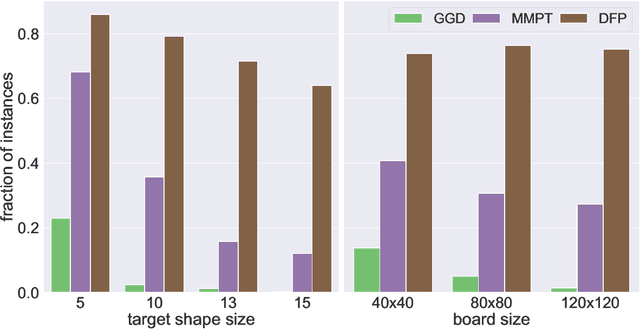
We investigate motion planning algorithms for the assembly of shapes in the \emph{tilt model} in which unit-square tiles move in a grid world under the influence of uniform external forces and self-assemble according to certain rules. We provide several heuristics and experimental evaluation of their success rate, solution length, runtime, and memory consumption.

Cooperative 2D Reconfiguration using Spatio-Temporal Planning and Load Transferring

We present progress on the problem of reconfiguring a 2D arrangement of building material by a cooperative set of robots. These robots are subjected to the constraints of avoiding obstacles and maintaining connectivity of the structure. We develop two reconfiguration methods, one based on spatio-temporal planning, and one based on target swapping. Both methods achieve coordinated motion of robots by avoiding deadlocks and maintaining all constraints. Both methods also increase efficiency by reducing the amount of waiting times and lowering combined travel costs. The resulting progress is validated by simulations that also scale the number of robots.

Connected Reconfiguration of Polyominoes Amid Obstacles using RRT*

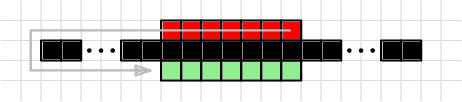
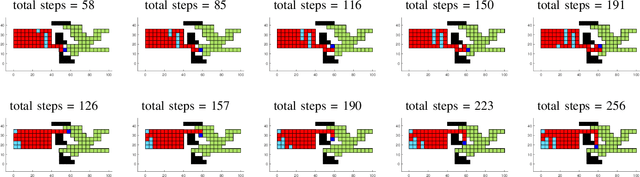
This paper investigates using a sampling-based approach, the RRT*, to reconfiguring a 2D set of connected tiles in complex environments, where multiple obstacles might be present. Since the target application is automated building of discrete, cellular structures using mobile robots, there are constraints that determine what tiles can be picked up and where they can be dropped off during reconfiguration. We compare our approach to two algorithms as global and local planners, and show that we are able to find more efficient build sequences using a reasonable amount of samples, in environments with varying degrees of obstacle space.

The Pursuit and Evasion of Drones Attacking an Automated Turret

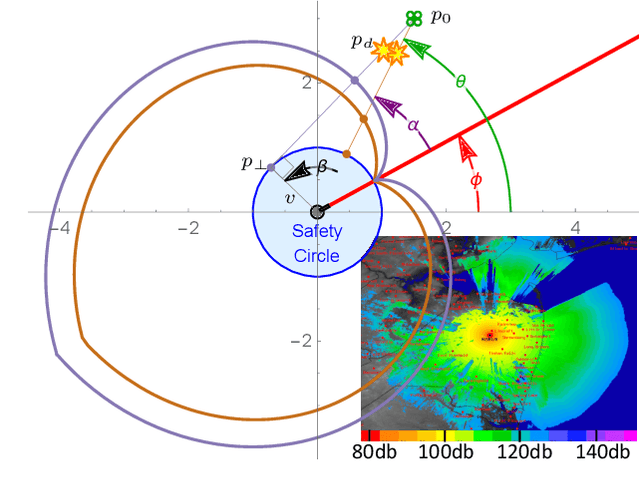
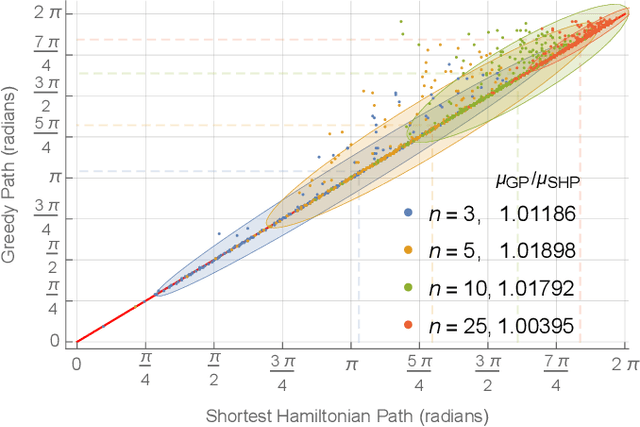
This paper investigates the pursuit-evasion problem of a defensive gun turret and one or more attacking drones. The turret must ``visit" each attacking drone once, as quickly as possible, to defeat the threat. This constitutes a Shortest Hamiltonian Path (SHP) through the drones. The investigation considers situations with increasing fidelity, starting with a 2D kinematic model and progressing to a 3D dynamic model. In 2D we determine the region from which one or more drones can always reach a turret, or the region close enough to it where they can evade the turret. This provides optimal starting angles for $n$ drones around a turret and the maximum starting radius for one and two drones. We show that safety regions also exist in 3D and provide a controller so that a drone in this region can evade the pan-tilt turret. Through simulations we explore the maximum range $n$ drones can start and still have at least one reach the turret, and analyze the effect of turret behavior and the drones' number, starting configuration, and behaviors.

Enumeration of Polyominoes & Polycubes Composed of Magnetic Cubes

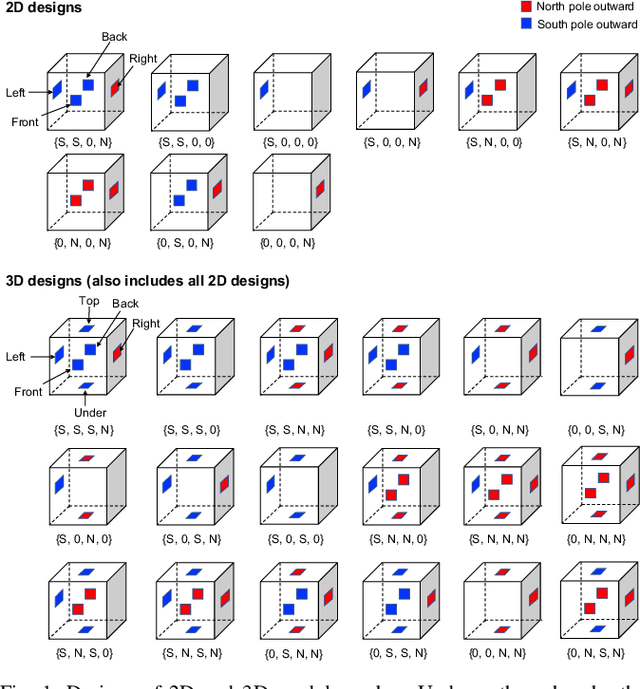
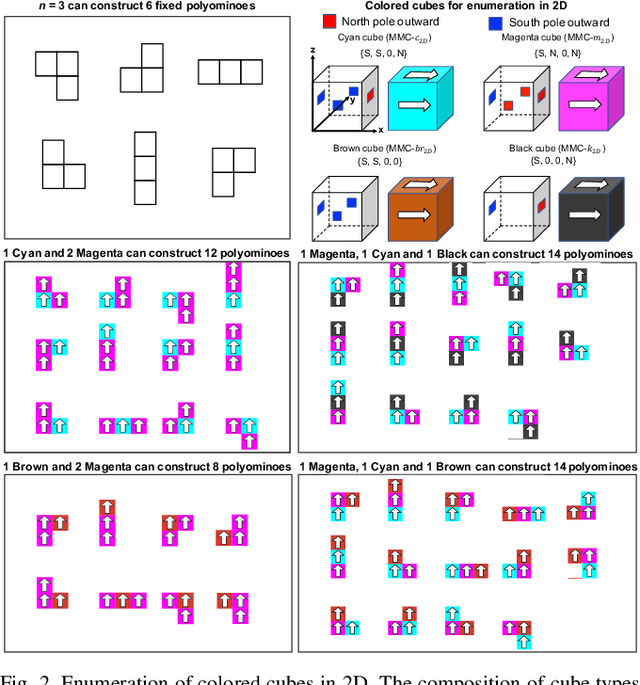
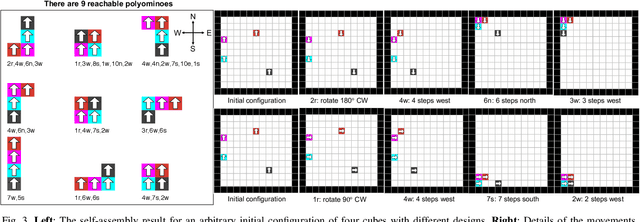
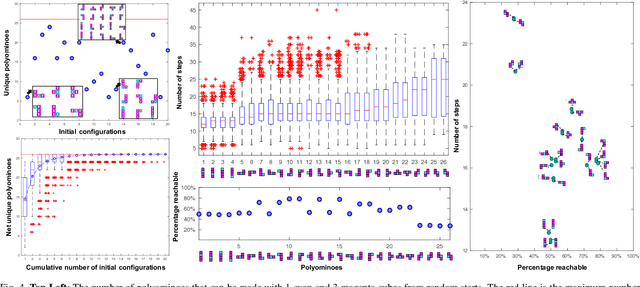
This paper examines a family of designs for magnetic cubes and counts how many configurations are possible for each design as a function of the number of modules. Magnetic modular cubes are cubes with magnets arranged on their faces. The magnets are positioned so that each face has either magnetic south or north pole outward. Moreover, we require that the net magnetic moment of the cube passes through the center of opposing faces. These magnetic arrangements enable coupling when cube faces with opposite polarity are brought in close proximity and enable moving the cubes by controlling the orientation of a global magnetic field. This paper investigates the 2D and 3D shapes that can be constructed by magnetic modular cubes, and describes all possible magnet arrangements that obey these rules. We select ten magnetic arrangements and assign a "colo"' to each of them for ease of visualization and reference. We provide a method to enumerate the number of unique polyominoes and polycubes that can be constructed from a given set of colored cubes. We use this method to enumerate all arrangements for up to 20 modules in 2D and 16 modules in 3D. We provide a motion planner for 2D assembly and through simulations compare which arrangements require fewer movements to generate and which arrangements are more common. Hardware demonstrations explore the self-assembly and disassembly of these modules in 2D and 3D.