Estimating Spatially-Dependent GPS Errors Using a Swarm of Robots

External factors, including urban canyons and adversarial interference, can lead to Global Positioning System (GPS) inaccuracies that vary as a function of the position in the environment. This study addresses the challenge of estimating a static, spatially-varying error function using a team of robots. We introduce a State Bias Estimation Algorithm (SBE) whose purpose is to estimate the GPS biases. The central idea is to use sensed estimates of the range and bearing to the other robots in the team to estimate changes in bias across the environment. A set of drones moves in a 2D environment, each sampling data from GPS, range, and bearing sensors. The biases calculated by the SBE at estimated positions are used to train a Gaussian Process Regression (GPR) model. We use a Sparse Gaussian process-based Informative Path Planning (IPP) algorithm that identifies high-value regions of the environment for data collection. The swarm plans paths that maximize information gain in each iteration, further refining their understanding of the environment's positional bias landscape. We evaluated SBE and IPP in simulation and compared the IPP methodology to an open-loop strategy.

An Analytic Solution to the 3D CSC Dubins Path Problem

We present an analytic solution to the 3D Dubins path problem for paths composed of an initial circular arc, a straight component, and a final circular arc. These are commonly called CSC paths. By modeling the start and goal configurations of the path as the base frame and final frame of an RRPRR manipulator, we treat this as an inverse kinematics problem. The kinematic features of the 3D Dubins path are built into the constraints of our manipulator model. Furthermore, we show that the number of solutions is not constant, with up to seven valid CSC path solutions even in non-singular regions. An implementation of solution is available at https://github.com/aabecker/dubins3D.

Minimum-Time Planar Paths with up to Two Constant Acceleration Inputs and $L_2$ Velocity and Acceleration Constraints

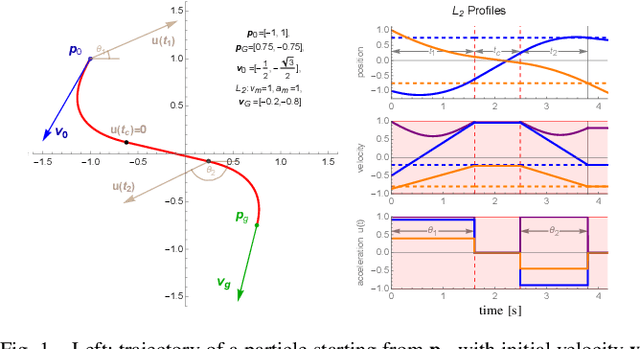
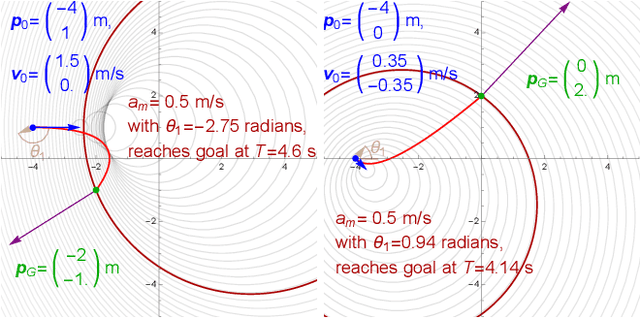
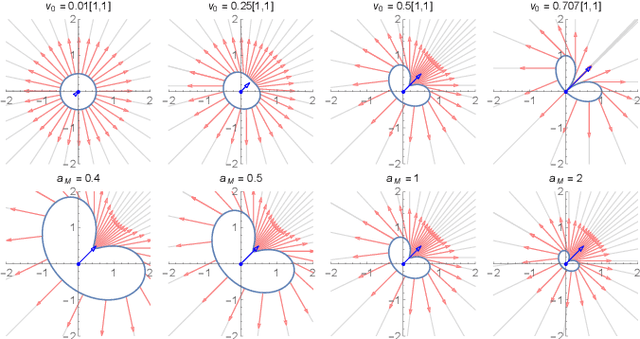
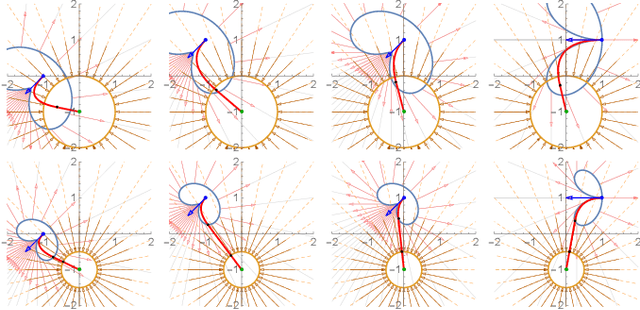
Given starting and ending positions and velocities, $L_2$ bounds on the acceleration and velocity, and the restriction to no more than two constant control inputs, this paper provides routines to compute the minimal-time path. Closed form solutions are provided for reaching a position in minimum time with and without a velocity bound, and for stopping at the goal position. A numeric solver is used to reach a goal position and velocity with no more than two constant control inputs. If a cruising phase at the terminal velocity is needed, this requires solving a non-linear equation with a single parameter. Code is provided on GitHub at https://github.com/RoboticSwarmControl/MinTimeL2pathsConstraints.