DoubleCCA: Improving Foundation Model Group Robustness with Random Sentence Embeddings

This paper presents a novel method to improve the robustness of foundation models to group-based biases. We propose a simple yet effective method, called DoubleCCA, that leverages random sentences and Canonical Correlation Analysis (CCA) to enrich the text embeddings of the foundation model. First, we generate various random sentences that augment the original prompts, which extends the original prompts with random words or character sequences. Second, we use an additional sentence embedding model to generate different text embeddings with respect to these random sentences. We then use CCA double twice to align the representations and reconstruct them back to the original representation space. We demonstrate the effectiveness of our method on a variety of tasks and datasets, showing that it outperforms existing methods in terms of both performance and robustness. Our method is simple to implement and can be easily integrated into existing models, making it a practical solution for improving the robustness of foundation models to group-based biases.

Enumeration of Polyominoes & Polycubes Composed of Magnetic Cubes

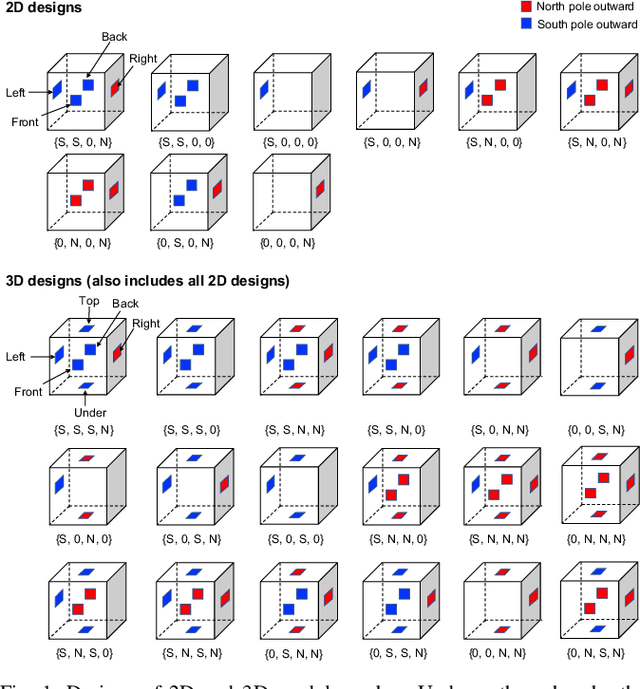
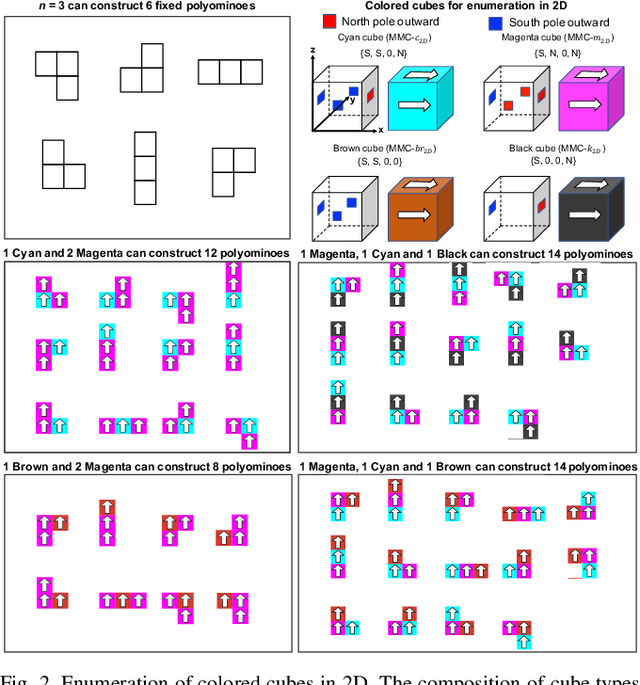
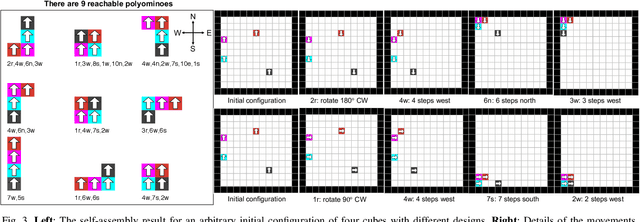
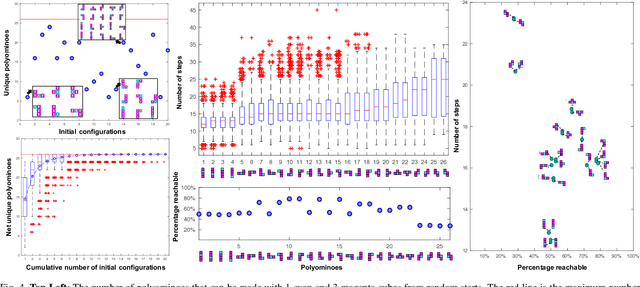
This paper examines a family of designs for magnetic cubes and counts how many configurations are possible for each design as a function of the number of modules. Magnetic modular cubes are cubes with magnets arranged on their faces. The magnets are positioned so that each face has either magnetic south or north pole outward. Moreover, we require that the net magnetic moment of the cube passes through the center of opposing faces. These magnetic arrangements enable coupling when cube faces with opposite polarity are brought in close proximity and enable moving the cubes by controlling the orientation of a global magnetic field. This paper investigates the 2D and 3D shapes that can be constructed by magnetic modular cubes, and describes all possible magnet arrangements that obey these rules. We select ten magnetic arrangements and assign a "colo"' to each of them for ease of visualization and reference. We provide a method to enumerate the number of unique polyominoes and polycubes that can be constructed from a given set of colored cubes. We use this method to enumerate all arrangements for up to 20 modules in 2D and 16 modules in 3D. We provide a motion planner for 2D assembly and through simulations compare which arrangements require fewer movements to generate and which arrangements are more common. Hardware demonstrations explore the self-assembly and disassembly of these modules in 2D and 3D.