Daniel Biediger
The Pursuit and Evasion of Drones Attacking an Automated Turret
Jul 27, 2021
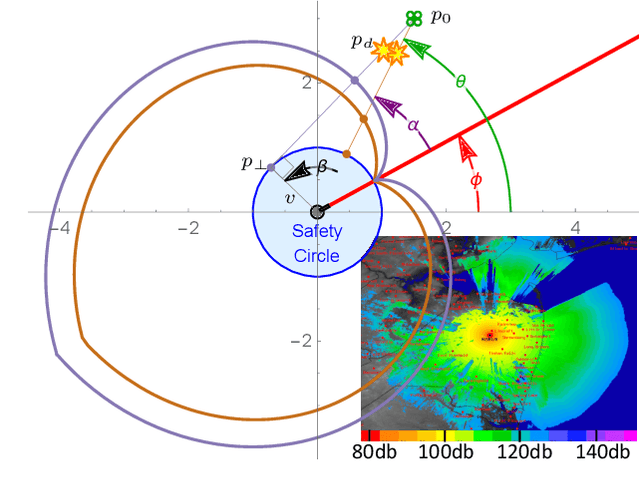
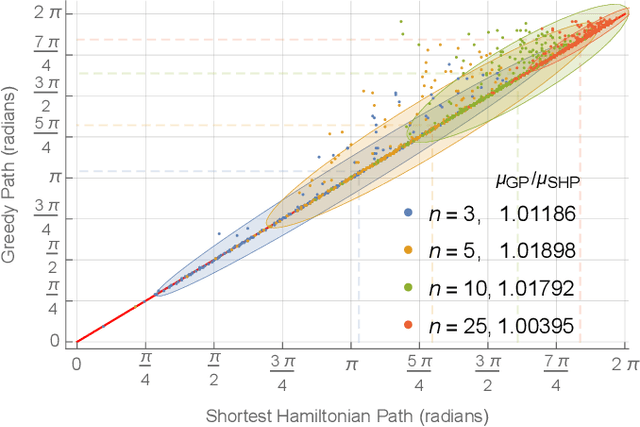

Abstract:This paper investigates the pursuit-evasion problem of a defensive gun turret and one or more attacking drones. The turret must ``visit" each attacking drone once, as quickly as possible, to defeat the threat. This constitutes a Shortest Hamiltonian Path (SHP) through the drones. The investigation considers situations with increasing fidelity, starting with a 2D kinematic model and progressing to a 3D dynamic model. In 2D we determine the region from which one or more drones can always reach a turret, or the region close enough to it where they can evade the turret. This provides optimal starting angles for $n$ drones around a turret and the maximum starting radius for one and two drones. We show that safety regions also exist in 3D and provide a controller so that a drone in this region can evade the pan-tilt turret. Through simulations we explore the maximum range $n$ drones can start and still have at least one reach the turret, and analyze the effect of turret behavior and the drones' number, starting configuration, and behaviors.
Enumeration of Polyominoes & Polycubes Composed of Magnetic Cubes
Jul 21, 2021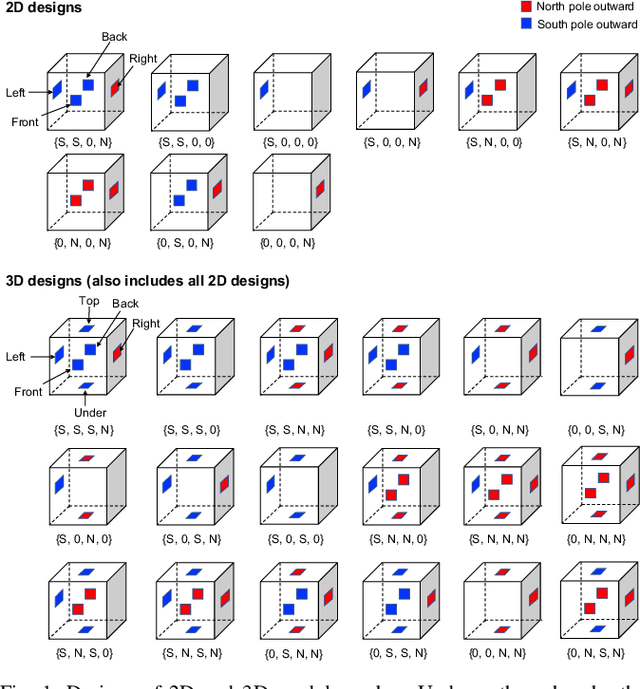
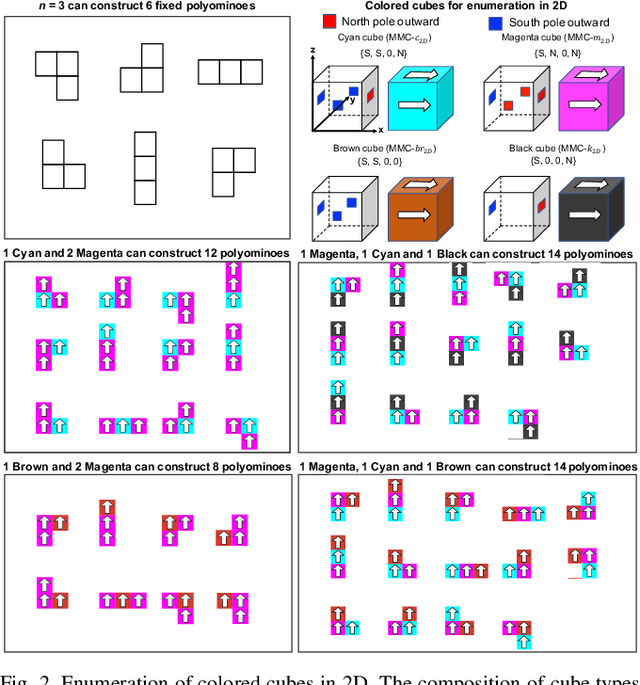
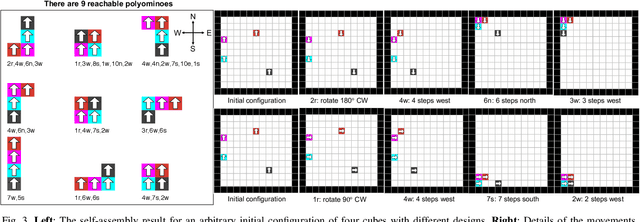
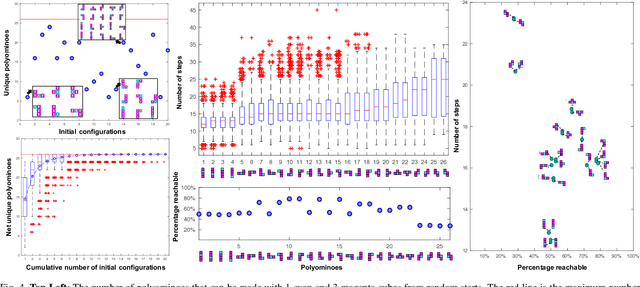
Abstract:This paper examines a family of designs for magnetic cubes and counts how many configurations are possible for each design as a function of the number of modules. Magnetic modular cubes are cubes with magnets arranged on their faces. The magnets are positioned so that each face has either magnetic south or north pole outward. Moreover, we require that the net magnetic moment of the cube passes through the center of opposing faces. These magnetic arrangements enable coupling when cube faces with opposite polarity are brought in close proximity and enable moving the cubes by controlling the orientation of a global magnetic field. This paper investigates the 2D and 3D shapes that can be constructed by magnetic modular cubes, and describes all possible magnet arrangements that obey these rules. We select ten magnetic arrangements and assign a "colo"' to each of them for ease of visualization and reference. We provide a method to enumerate the number of unique polyominoes and polycubes that can be constructed from a given set of colored cubes. We use this method to enumerate all arrangements for up to 20 modules in 2D and 16 modules in 3D. We provide a motion planner for 2D assembly and through simulations compare which arrangements require fewer movements to generate and which arrangements are more common. Hardware demonstrations explore the self-assembly and disassembly of these modules in 2D and 3D.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge