Luben Popov
The Pursuit and Evasion of Drones Attacking an Automated Turret
Jul 27, 2021
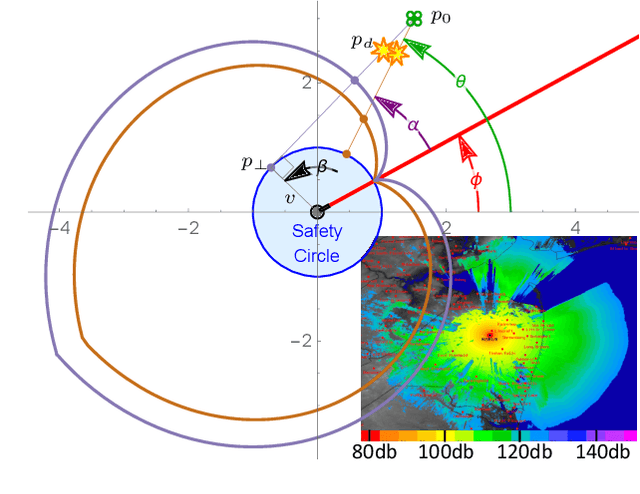
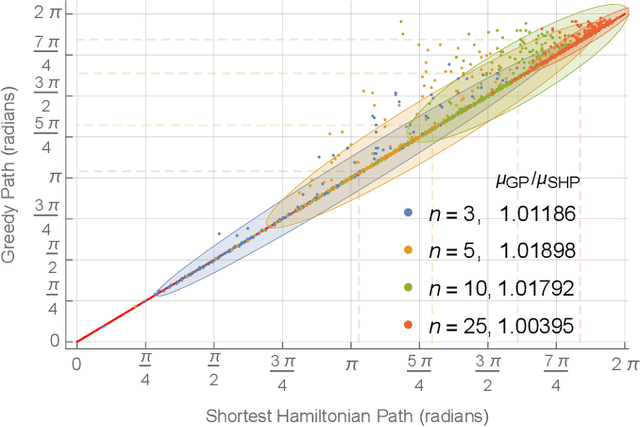

Abstract:This paper investigates the pursuit-evasion problem of a defensive gun turret and one or more attacking drones. The turret must ``visit" each attacking drone once, as quickly as possible, to defeat the threat. This constitutes a Shortest Hamiltonian Path (SHP) through the drones. The investigation considers situations with increasing fidelity, starting with a 2D kinematic model and progressing to a 3D dynamic model. In 2D we determine the region from which one or more drones can always reach a turret, or the region close enough to it where they can evade the turret. This provides optimal starting angles for $n$ drones around a turret and the maximum starting radius for one and two drones. We show that safety regions also exist in 3D and provide a controller so that a drone in this region can evade the pan-tilt turret. Through simulations we explore the maximum range $n$ drones can start and still have at least one reach the turret, and analyze the effect of turret behavior and the drones' number, starting configuration, and behaviors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge