Moving Matter: Efficient Reconfiguration of Tile Arrangements by a Single Active Robot
Paper and Code
Feb 13, 2025
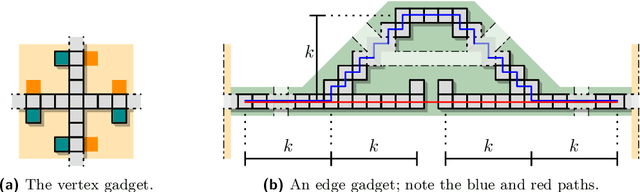
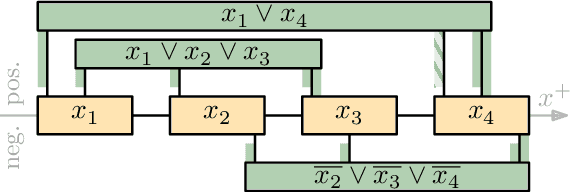
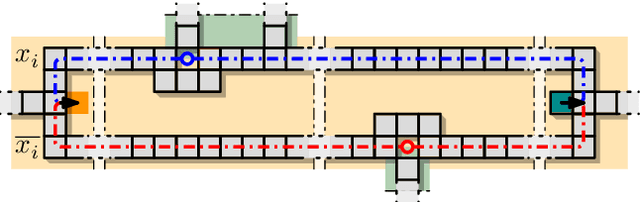
We consider the problem of reconfiguring a two-dimensional connected grid arrangement of passive building blocks from a start configuration to a goal configuration, using a single active robot that can move on the tiles, remove individual tiles from a given location and physically move them to a new position by walking on the remaining configuration. The objective is to determine a reconfiguration schedule that minimizes the overall makespan, while ensuring that the tile configuration remains connected. We provide both negative and positive results. (1) We present a generalized version of the problem, parameterized by weighted costs for moving with or without tiles, and show that this is NP-complete. (2) We give a polynomial-time constant-factor approximation algorithm for the case of disjoint start and target bounding boxes. In addition, our approach yields optimal carry distance for 2-scaled instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge