Peter Kramer
Moving Matter: Efficient Reconfiguration of Tile Arrangements by a Single Active Robot
Feb 13, 2025Abstract:We consider the problem of reconfiguring a two-dimensional connected grid arrangement of passive building blocks from a start configuration to a goal configuration, using a single active robot that can move on the tiles, remove individual tiles from a given location and physically move them to a new position by walking on the remaining configuration. The objective is to determine a reconfiguration schedule that minimizes the overall makespan, while ensuring that the tile configuration remains connected. We provide both negative and positive results. (1) We present a generalized version of the problem, parameterized by weighted costs for moving with or without tiles, and show that this is NP-complete. (2) We give a polynomial-time constant-factor approximation algorithm for the case of disjoint start and target bounding boxes. In addition, our approach yields optimal carry distance for 2-scaled instances.
Cooperative 2D Reconfiguration using Spatio-Temporal Planning and Load Transferring
Nov 16, 2022



Abstract:We present progress on the problem of reconfiguring a 2D arrangement of building material by a cooperative set of robots. These robots are subjected to the constraints of avoiding obstacles and maintaining connectivity of the structure. We develop two reconfiguration methods, one based on spatio-temporal planning, and one based on target swapping. Both methods achieve coordinated motion of robots by avoiding deadlocks and maintaining all constraints. Both methods also increase efficiency by reducing the amount of waiting times and lowering combined travel costs. The resulting progress is validated by simulations that also scale the number of robots.
Efficiently Reconfiguring a Connected Swarm of Labeled Robots
Sep 22, 2022

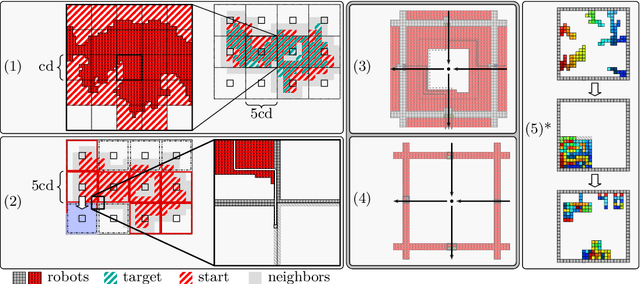
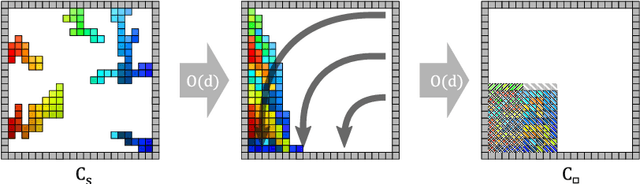
Abstract:When considering motion planning for a swarm of $n$ labeled robots, we need to rearrange a given start configuration into a desired target configuration via a sequence of parallel, continuous, collision-free robot motions. The objective is to reach the new configuration in a minimum amount of time; an important constraint is to keep the swarm connected at all times. Problems of this type have been considered before, with recent notable results achieving constant stretch for not necessarily connected reconfiguration: If mapping the start configuration to the target configuration requires a maximum Manhattan distance of $d$, the total duration of an overall schedule can be bounded to $\mathcal{O}(d)$, which is optimal up to constant factors. However, constant stretch could only be achieved if disconnected reconfiguration is allowed, or for scaled configurations (which arise by increasing all dimensions of a given object by the same multiplicative factor) of unlabeled robots. We resolve these major open problems by (1) establishing a lower bound of $\Omega(\sqrt{n})$ for connected, labeled reconfiguration and, most importantly, by (2) proving that for scaled arrangements, constant stretch for connected reconfiguration can be achieved. In addition, we show that (3) it is NP-hard to decide whether a makespan of 2 can be achieved, while it is possible to check in polynomial time whether a makespan of 1 can be achieved.
Connected Reconfiguration of Polyominoes Amid Obstacles using RRT*
Jul 04, 2022

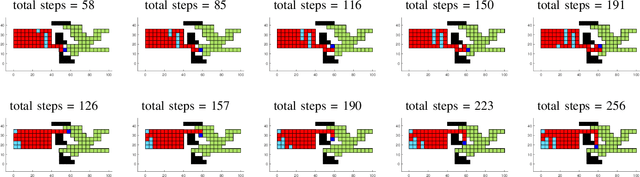
Abstract:This paper investigates using a sampling-based approach, the RRT*, to reconfiguring a 2D set of connected tiles in complex environments, where multiple obstacles might be present. Since the target application is automated building of discrete, cellular structures using mobile robots, there are constraints that determine what tiles can be picked up and where they can be dropped off during reconfiguration. We compare our approach to two algorithms as global and local planners, and show that we are able to find more efficient build sequences using a reasonable amount of samples, in environments with varying degrees of obstacle space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge