Computing Coordinated Motion Plans for Robot Swarms: The CG:SHOP Challenge 2021

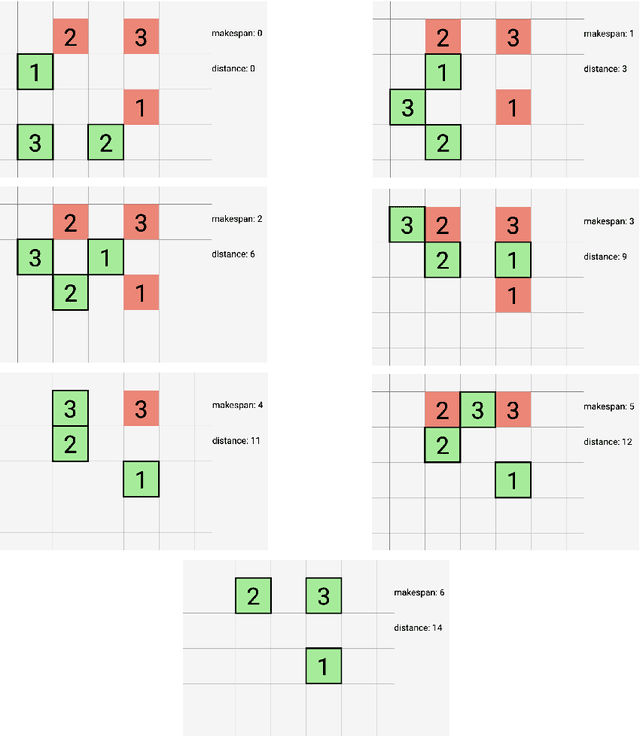
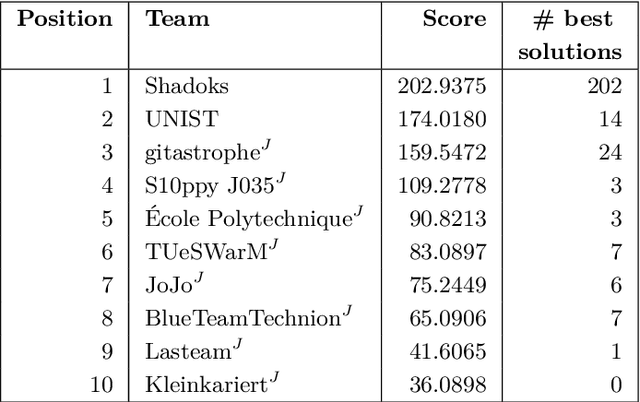
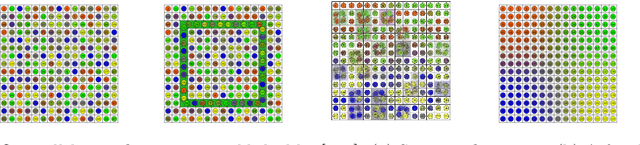
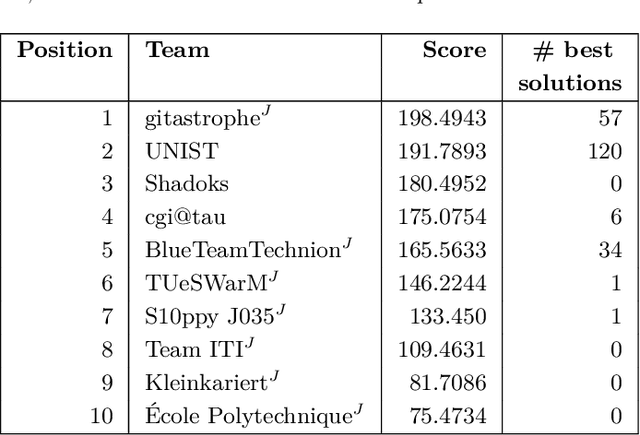
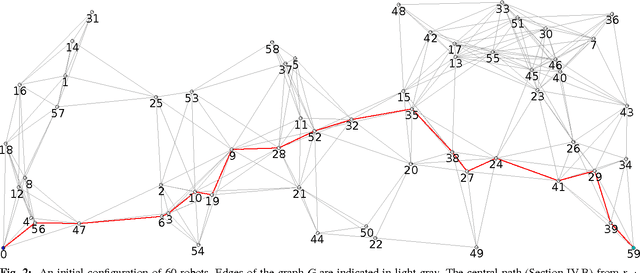
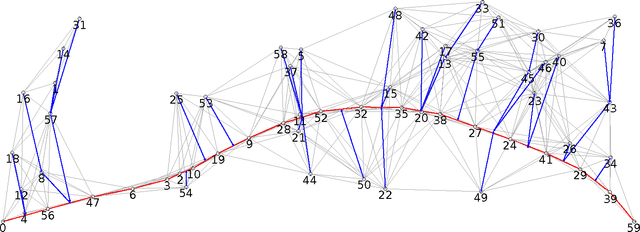
We give an overview of the 2021 Computational Geometry Challenge, which targeted the problem of optimally coordinating a set of robots by computing a family of collision-free trajectories for a set set S of n pixel-shaped objects from a given start configuration into a desired target configuration.

Collecting a Swarm in a Grid Environment Using Shared, Global Inputs

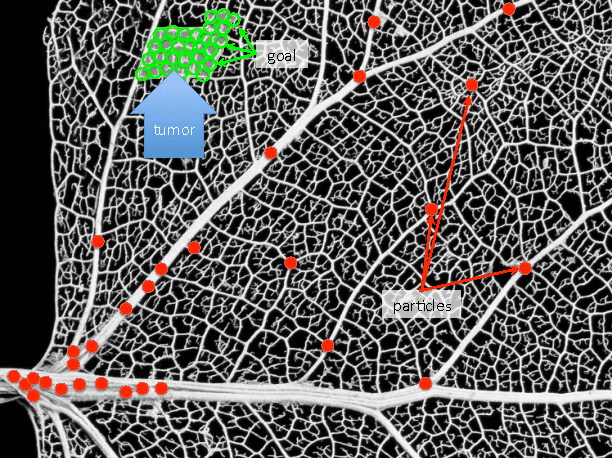
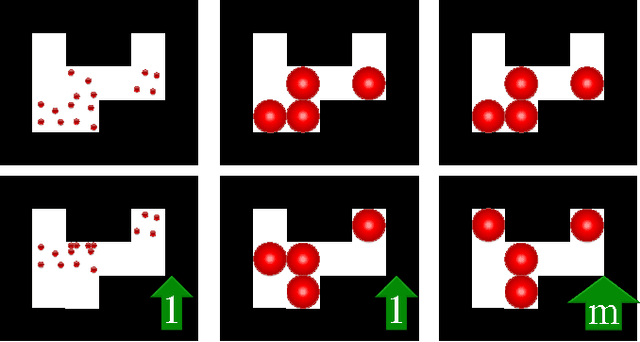
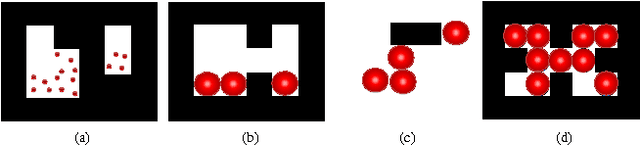
This paper investigates efficient techniques to collect and concentrate an under-actuated particle swarm despite obstacles. Concentrating a swarm of particles is of critical importance in health-care for targeted drug delivery, where micro-scale particles must be steered to a goal location. Individual particles must be small in order to navigate through micro-vasculature, but decreasing size brings new challenges. Individual particles are too small to contain on-board power or computation and are instead controlled by a global input, such as an applied fluidic flow or electric field. To make progress, this paper considers a swarm of robots initialized in a grid world in which each position is either free-space or obstacle. This paper provides algorithms that collect all the robots to one position and compares these algorithms on the basis of efficiency and implementation time.

A Parallel Distributed Strategy for Arraying a Scattered Robot Swarm

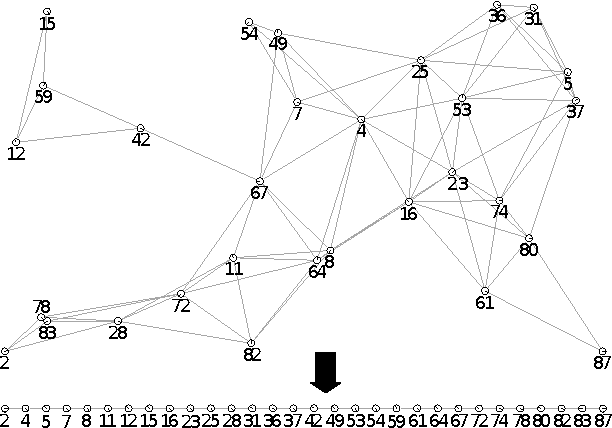
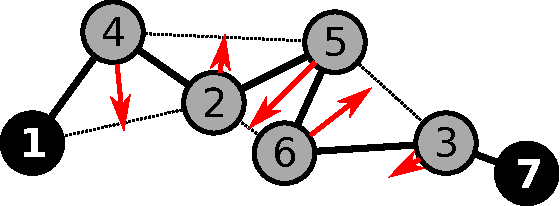
We consider the problem of organizing a scattered group of $n$ robots in two-dimensional space, with geometric maximum distance $D$ between robots. The communication graph of the swarm is connected, but there is no central authority for organizing it. We want to arrange them into a sorted and equally-spaced array between the robots with lowest and highest label, while maintaining a connected communication network. In this paper, we describe a distributed method to accomplish these goals, without using central control, while also keeping time, travel distance and communication cost at a minimum. We proceed in a number of stages (leader election, initial path construction, subtree contraction, geometric straightening, and distributed sorting), none of which requires a central authority, but still accomplishes best possible parallelization. The overall arraying is performed in $O(n)$ time, $O(n^2)$ individual messages, and $O(nD)$ travel distance. Implementation of the sorting and navigation use communication messages of fixed size, and are a practical solution for large populations of low-cost robots.

Distributed Cohesive Control for Robot Swarms: Maintaining Good Connectivity in the Presence of Exterior Forces

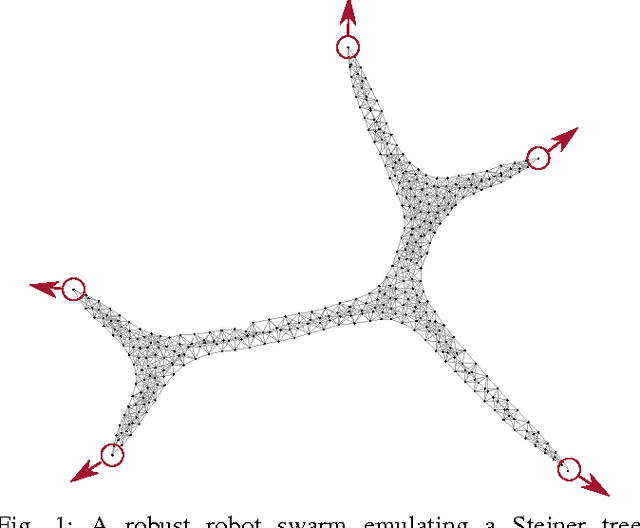
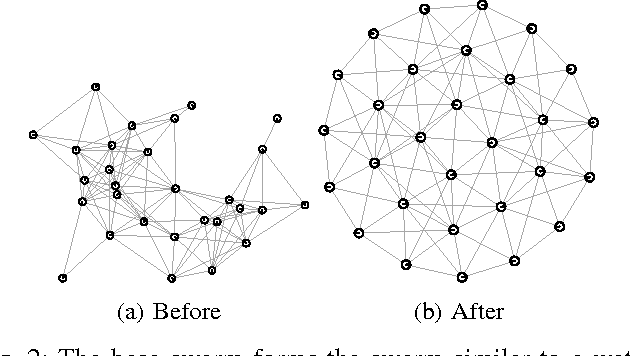
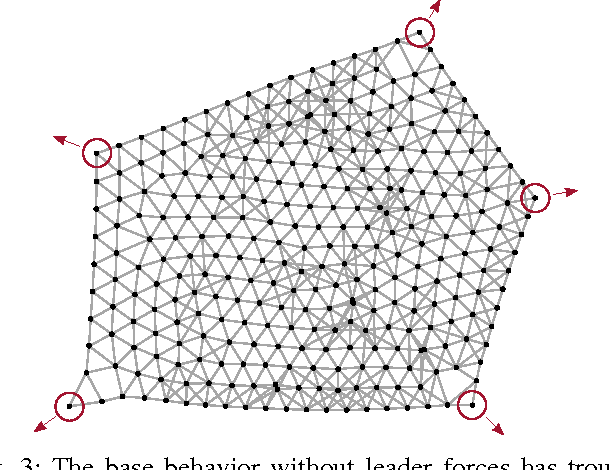
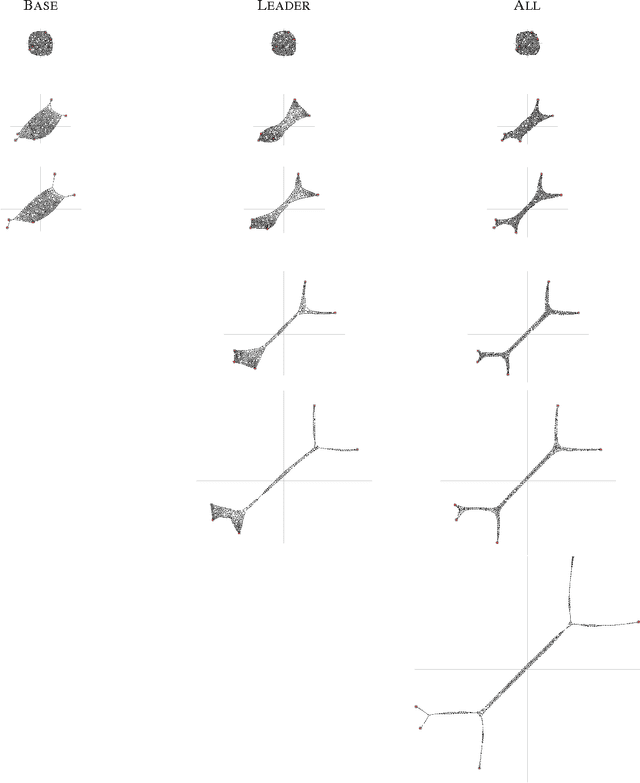
We present a number of powerful local mechanisms for maintaining a dynamic swarm of robots with limited capabilities and information, in the presence of external forces and permanent node failures. We propose a set of local continuous algorithms that together produce a generalization of a Euclidean Steiner tree. At any stage, the resulting overall shape achieves a good compromise between local thickness, global connectivity, and flexibility to further continuous motion of the terminals. The resulting swarm behavior scales well, is robust against node failures, and performs close to the best known approximation bound for a corresponding centralized static optimization problem.