Exploring Grid Polygons Online

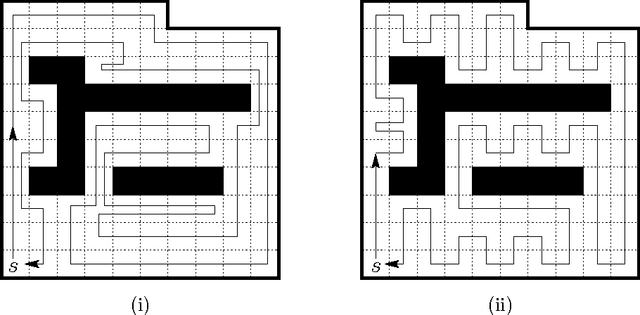
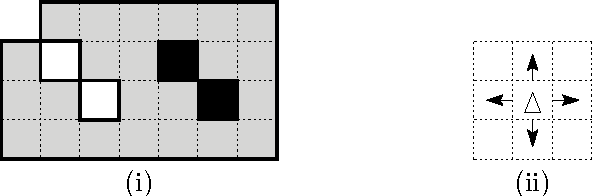
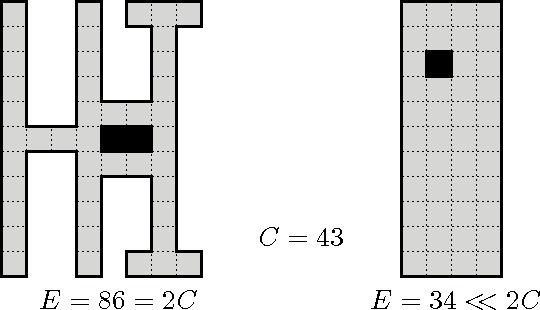
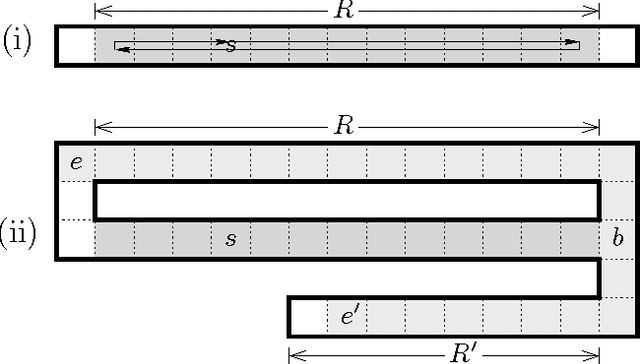
We investigate the exploration problem of a short-sighted mobile robot moving in an unknown cellular room. To explore a cell, the robot must enter it. Once inside, the robot knows which of the 4 adjacent cells exist and which are boundary edges. The robot starts from a specified cell adjacent to the room's outer wall; it visits each cell, and returns to the start. Our interest is in a short exploration tour; that is, in keeping the number of multiple cell visits small. For abitrary environments containing no obstacles we provide a strategy producing tours of length S <= C + 1/2 E - 3, and for environments containing obstacles we provide a strategy, that is bound by S <= C + 1/2 E + 3H + WCW - 2, where C denotes the number of cells-the area-, E denotes the number of boundary edges-the perimeter-, and H is the number of obstacles, and WCW is a measure for the sinuosity of the given environment.

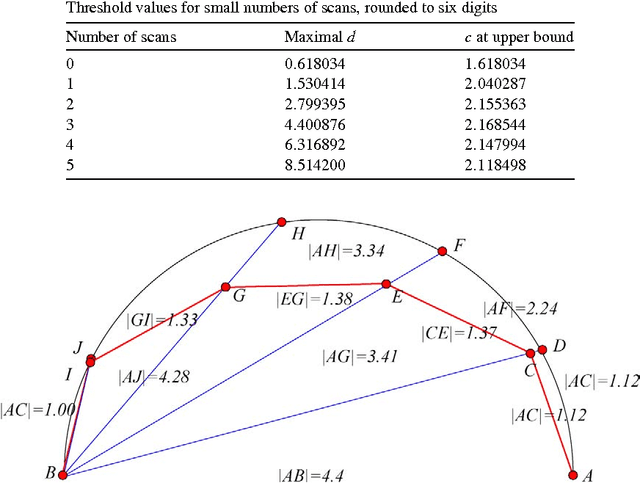
Online Searching with an Autonomous Robot

We discuss online strategies for visibility-based searching for an object hidden behind a corner, using Kurt3D, a real autonomous mobile robot. This task is closely related to a number of well-studied problems. Our robot uses a three-dimensional laser scanner in a stop, scan, plan, go fashion for building a virtual three-dimensional environment. Besides planning trajectories and avoiding obstacles, Kurt3D is capable of identifying objects like a chair. We derive a practically useful and asymptotically optimal strategy that guarantees a competitive ratio of 2, which differs remarkably from the well-studied scenario without the need of stopping for surveying the environment. Our strategy is used by Kurt3D, documented in a separate video.