Evolutionary learning of fire fighting strategies

The dynamic problem of enclosing an expanding fire can be modelled by a discrete variant in a grid graph. While the fire expands to all neighbouring cells in any time step, the fire fighter is allowed to block $c$ cells in the average outside the fire in the same time interval. It was shown that the success of the fire fighter is guaranteed for $c>1.5$ but no strategy can enclose the fire for $c\leq 1.5$. For achieving such a critical threshold the correctness (sometimes even optimality) of strategies and lower bounds have been shown by integer programming or by direct but often very sophisticated arguments. We investigate the problem whether it is possible to find or to approach such a threshold and/or optimal strategies by means of evolutionary algorithms, i.e., we just try to learn successful strategies for different constants $c$ and have a look at the outcome. The main general idea is that this approach might give some insight in the power of evolutionary strategies for similar geometrically motivated threshold questions. We investigate the variant of protecting a highway with still unknown threshold and found interesting strategic paradigms. Keywords: Dynamic environments, fire fighting, evolutionary strategies, threshold approximation

Exploring Simple Triangular and Hexagonal Grid Polygons Online

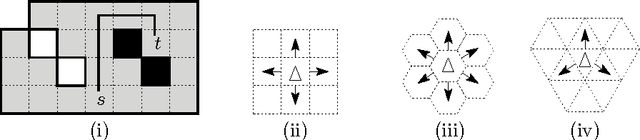
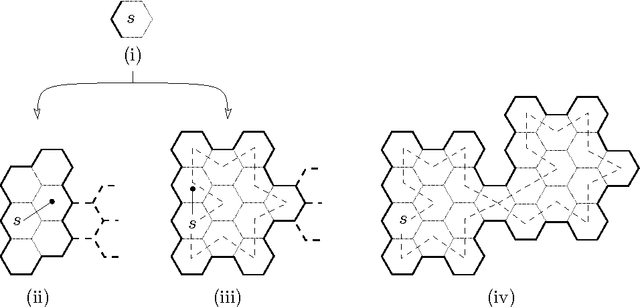
We investigate the online exploration problem (aka covering) of a short-sighted mobile robot moving in an unknown cellular environment with hexagons and triangles as types of cells. To explore a cell, the robot must enter it. Once inside, the robot knows which of the 3 or 6 adjacent cells exist and which are boundary edges. The robot's task is to visit every cell in the given environment and to return to the start. Our interest is in a short exploration tour; that is, in keeping the number of multiple cell visits small. For arbitrary environments containing no obstacles we provide a strategy producing tours of length S <= C + 1/4 E - 2.5 for hexagonal grids, and S <= C + E - 4 for triangular grids. C denotes the number of cells-the area-, E denotes the number of boundary edges-the perimeter-of the given environment. Further, we show that our strategy is 4/3-competitive in both types of grids, and we provide lower bounds of 14/13 for hexagonal grids and 7/6 for triangular grids.

Exploring Grid Polygons Online

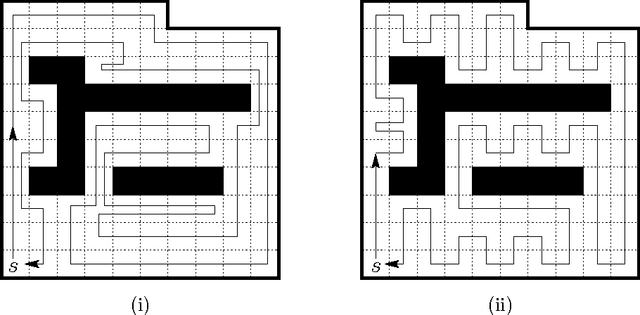
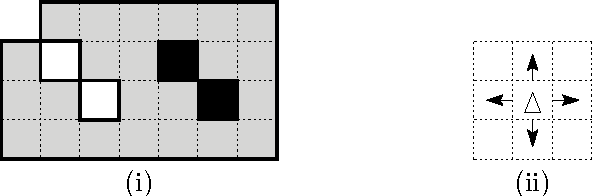
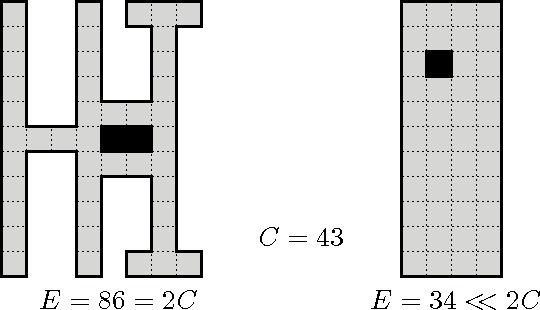
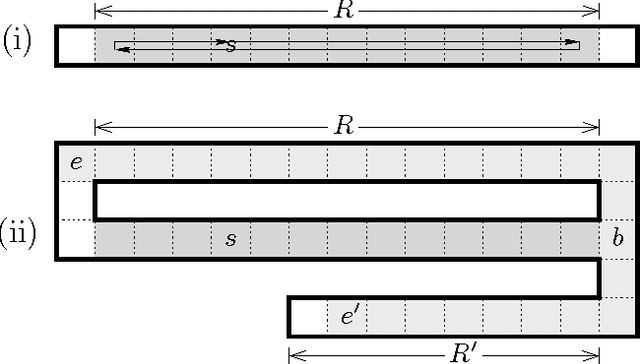
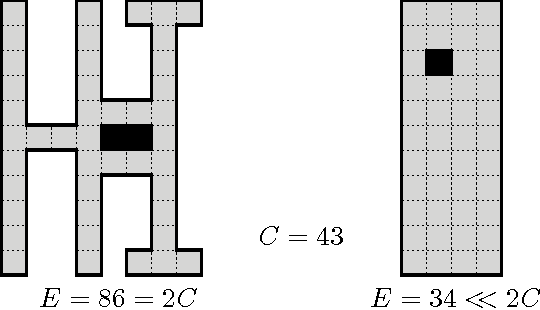
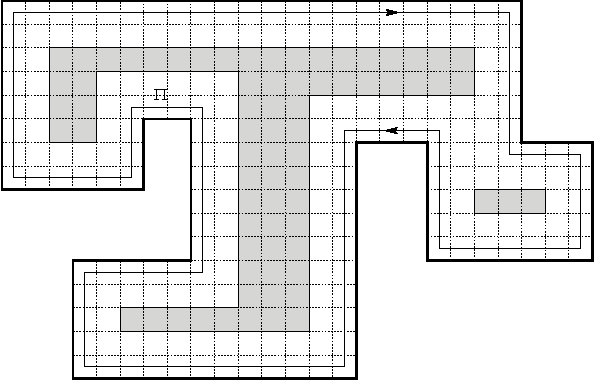
We investigate the exploration problem of a short-sighted mobile robot moving in an unknown cellular room. To explore a cell, the robot must enter it. Once inside, the robot knows which of the 4 adjacent cells exist and which are boundary edges. The robot starts from a specified cell adjacent to the room's outer wall; it visits each cell, and returns to the start. Our interest is in a short exploration tour; that is, in keeping the number of multiple cell visits small. For abitrary environments containing no obstacles we provide a strategy producing tours of length S <= C + 1/2 E - 3, and for environments containing obstacles we provide a strategy, that is bound by S <= C + 1/2 E + 3H + WCW - 2, where C denotes the number of cells-the area-, E denotes the number of boundary edges-the perimeter-, and H is the number of obstacles, and WCW is a measure for the sinuosity of the given environment.