Exploring Simple Triangular and Hexagonal Grid Polygons Online

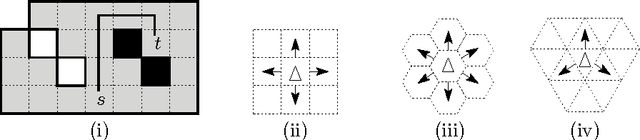
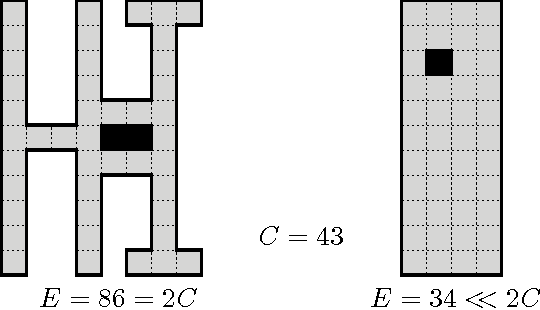
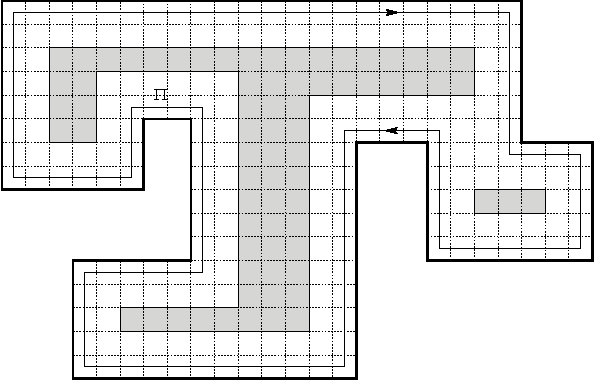
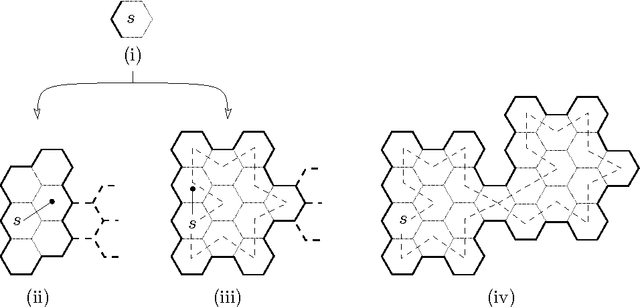
We investigate the online exploration problem (aka covering) of a short-sighted mobile robot moving in an unknown cellular environment with hexagons and triangles as types of cells. To explore a cell, the robot must enter it. Once inside, the robot knows which of the 3 or 6 adjacent cells exist and which are boundary edges. The robot's task is to visit every cell in the given environment and to return to the start. Our interest is in a short exploration tour; that is, in keeping the number of multiple cell visits small. For arbitrary environments containing no obstacles we provide a strategy producing tours of length S <= C + 1/4 E - 2.5 for hexagonal grids, and S <= C + E - 4 for triangular grids. C denotes the number of cells-the area-, E denotes the number of boundary edges-the perimeter-of the given environment. Further, we show that our strategy is 4/3-competitive in both types of grids, and we provide lower bounds of 14/13 for hexagonal grids and 7/6 for triangular grids.

Reliable and Efficient Inference of Bayesian Networks from Sparse Data by Statistical Learning Theory

To learn (statistical) dependencies among random variables requires exponentially large sample size in the number of observed random variables if any arbitrary joint probability distribution can occur. We consider the case that sparse data strongly suggest that the probabilities can be described by a simple Bayesian network, i.e., by a graph with small in-degree \Delta. Then this simple law will also explain further data with high confidence. This is shown by calculating bounds on the VC dimension of the set of those probability measures that correspond to simple graphs. This allows to select networks by structural risk minimization and gives reliability bounds on the error of the estimated joint measure without (in contrast to a previous paper) any prior assumptions on the set of possible joint measures. The complexity for searching the optimal Bayesian networks of in-degree \Delta increases only polynomially in the number of random varibales for constant \Delta and the optimal joint measure associated with a given graph can be found by convex optimization.