From Guess2Graph: When and How Can Unreliable Experts Safely Boost Causal Discovery in Finite Samples?

Causal discovery algorithms often perform poorly with limited samples. While integrating expert knowledge (including from LLMs) as constraints promises to improve performance, guarantees for existing methods require perfect predictions or uncertainty estimates, making them unreliable for practical use. We propose the Guess2Graph (G2G) framework, which uses expert guesses to guide the sequence of statistical tests rather than replacing them. This maintains statistical consistency while enabling performance improvements. We develop two instantiations of G2G: PC-Guess, which augments the PC algorithm, and gPC-Guess, a learning-augmented variant designed to better leverage high-quality expert input. Theoretically, both preserve correctness regardless of expert error, with gPC-Guess provably outperforming its non-augmented counterpart in finite samples when experts are "better than random." Empirically, both show monotonic improvement with expert accuracy, with gPC-Guess achieving significantly stronger gains.

Root Cause Analysis of Outliers in Unknown Cyclic Graphs

We study the propagation of outliers in cyclic causal graphs with linear structural equations, tracing them back to one or several "root cause" nodes. We show that it is possible to identify a short list of potential root causes provided that the perturbation is sufficiently strong and propagates according to the same structural equations as in the normal mode. This shortlist consists of the true root causes together with those of its parents lying on a cycle with the root cause. Notably, our method does not require prior knowledge of the causal graph.

On Different Notions of Redundancy in Conditional-Independence-Based Discovery of Graphical Models

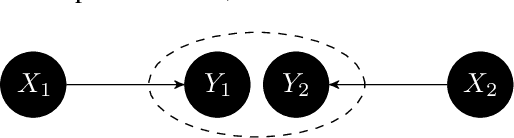
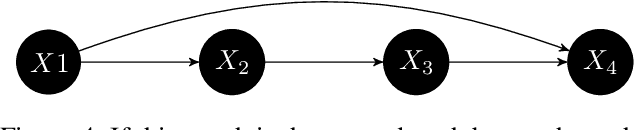
The goal of conditional-independence-based discovery of graphical models is to find a graph that represents the independence structure of variables in a given dataset. To learn such a representation, conditional-independence-based approaches conduct a set of statistical tests that suffices to identify the graphical representation under some assumptions on the underlying distribution of the data. In this work, we highlight that due to the conciseness of the graphical representation, there are often many tests that are not used in the construction of the graph. These redundant tests have the potential to detect or sometimes correct errors in the learned model. We show that not all tests contain this additional information and that such redundant tests have to be applied with care. Precisely, we argue that particularly those conditional (in)dependence statements are interesting that follow only from graphical assumptions but do not hold for every probability distribution.

Toward Universal Laws of Outlier Propagation

We argue that Algorithmic Information Theory (AIT) admits a principled way to quantify outliers in terms of so-called randomness deficiency. For the probability distribution generated by a causal Bayesian network, we show that the randomness deficiency of the joint state decomposes into randomness deficiencies of each causal mechanism, subject to the Independence of Mechanisms Principle. Accordingly, anomalous joint observations can be quantitatively attributed to their root causes, i.e., the mechanisms that behaved anomalously. As an extension of Levin's law of randomness conservation, we show that weak outliers cannot cause strong ones when Independence of Mechanisms holds. We show how these information theoretic laws provide a better understanding of the behaviour of outliers defined with respect to existing scores.

Causal vs. Anticausal merging of predictors

We study the differences arising from merging predictors in the causal and anticausal directions using the same data. In particular we study the asymmetries that arise in a simple model where we merge the predictors using one binary variable as target and two continuous variables as predictors. We use Causal Maximum Entropy (CMAXENT) as inductive bias to merge the predictors, however, we expect similar differences to hold also when we use other merging methods that take into account asymmetries between cause and effect. We show that if we observe all bivariate distributions, the CMAXENT solution reduces to a logistic regression in the causal direction and Linear Discriminant Analysis (LDA) in the anticausal direction. Furthermore, we study how the decision boundaries of these two solutions differ whenever we observe only some of the bivariate distributions implications for Out-Of-Variable (OOV) generalisation.

Cross-validating causal discovery via Leave-One-Variable-Out

We propose a new approach to falsify causal discovery algorithms without ground truth, which is based on testing the causal model on a pair of variables that has been dropped when learning the causal model. To this end, we use the "Leave-One-Variable-Out (LOVO)" prediction where $Y$ is inferred from $X$ without any joint observations of $X$ and $Y$, given only training data from $X,Z_1,\dots,Z_k$ and from $Z_1,\dots,Z_k,Y$. We demonstrate that causal models on the two subsets, in the form of Acyclic Directed Mixed Graphs (ADMGs), often entail conclusions on the dependencies between $X$ and $Y$, enabling this type of prediction. The prediction error can then be estimated since the joint distribution $P(X, Y)$ is assumed to be available, and $X$ and $Y$ have only been omitted for the purpose of falsification. After presenting this graphical method, which is applicable to general causal discovery algorithms, we illustrate how to construct a LOVO predictor tailored towards algorithms relying on specific a priori assumptions, such as linear additive noise models. Simulations indicate that the LOVO prediction error is indeed correlated with the accuracy of the causal outputs, affirming the method's effectiveness.

Root Cause Analysis of Outliers with Missing Structural Knowledge

Recent work conceptualized root cause analysis (RCA) of anomalies via quantitative contribution analysis using causal counterfactuals in structural causal models (SCMs). The framework comes with three practical challenges: (1) it requires the causal directed acyclic graph (DAG), together with an SCM, (2) it is statistically ill-posed since it probes regression models in regions of low probability density, (3) it relies on Shapley values which are computationally expensive to find. In this paper, we propose simplified, efficient methods of root cause analysis when the task is to identify a unique root cause instead of quantitative contribution analysis. Our proposed methods run in linear order of SCM nodes and they require only the causal DAG without counterfactuals. Furthermore, for those use cases where the causal DAG is unknown, we justify the heuristic of identifying root causes as the variables with the highest anomaly score.

Multiply-Robust Causal Change Attribution

Comparing two samples of data, we observe a change in the distribution of an outcome variable. In the presence of multiple explanatory variables, how much of the change can be explained by each possible cause? We develop a new estimation strategy that, given a causal model, combines regression and re-weighting methods to quantify the contribution of each causal mechanism. Our proposed methodology is multiply robust, meaning that it still recovers the target parameter under partial misspecification. We prove that our estimator is consistent and asymptotically normal. Moreover, it can be incorporated into existing frameworks for causal attribution, such as Shapley values, which will inherit the consistency and large-sample distribution properties. Our method demonstrates excellent performance in Monte Carlo simulations, and we show its usefulness in an empirical application.

Assumption violations in causal discovery and the robustness of score matching

When domain knowledge is limited and experimentation is restricted by ethical, financial, or time constraints, practitioners turn to observational causal discovery methods to recover the causal structure, exploiting the statistical properties of their data. Because causal discovery without further assumptions is an ill-posed problem, each algorithm comes with its own set of usually untestable assumptions, some of which are hard to meet in real datasets. Motivated by these considerations, this paper extensively benchmarks the empirical performance of recent causal discovery methods on observational i.i.d. data generated under different background conditions, allowing for violations of the critical assumptions required by each selected approach. Our experimental findings show that score matching-based methods demonstrate surprising performance in the false positive and false negative rate of the inferred graph in these challenging scenarios, and we provide theoretical insights into their performance. This work is also the first effort to benchmark the stability of causal discovery algorithms with respect to the values of their hyperparameters. Finally, we hope this paper will set a new standard for the evaluation of causal discovery methods and can serve as an accessible entry point for practitioners interested in the field, highlighting the empirical implications of different algorithm choices.

Self-Compatibility: Evaluating Causal Discovery without Ground Truth

As causal ground truth is incredibly rare, causal discovery algorithms are commonly only evaluated on simulated data. This is concerning, given that simulations reflect common preconceptions about generating processes regarding noise distributions, model classes, and more. In this work, we propose a novel method for falsifying the output of a causal discovery algorithm in the absence of ground truth. Our key insight is that while statistical learning seeks stability across subsets of data points, causal learning should seek stability across subsets of variables. Motivated by this insight, our method relies on a notion of compatibility between causal graphs learned on different subsets of variables. We prove that detecting incompatibilities can falsify wrongly inferred causal relations due to violation of assumptions or errors from finite sample effects. Although passing such compatibility tests is only a necessary criterion for good performance, we argue that it provides strong evidence for the causal models whenever compatibility entails strong implications for the joint distribution. We also demonstrate experimentally that detection of incompatibilities can aid in causal model selection.