Assumption violations in causal discovery and the robustness of score matching

When domain knowledge is limited and experimentation is restricted by ethical, financial, or time constraints, practitioners turn to observational causal discovery methods to recover the causal structure, exploiting the statistical properties of their data. Because causal discovery without further assumptions is an ill-posed problem, each algorithm comes with its own set of usually untestable assumptions, some of which are hard to meet in real datasets. Motivated by these considerations, this paper extensively benchmarks the empirical performance of recent causal discovery methods on observational i.i.d. data generated under different background conditions, allowing for violations of the critical assumptions required by each selected approach. Our experimental findings show that score matching-based methods demonstrate surprising performance in the false positive and false negative rate of the inferred graph in these challenging scenarios, and we provide theoretical insights into their performance. This work is also the first effort to benchmark the stability of causal discovery algorithms with respect to the values of their hyperparameters. Finally, we hope this paper will set a new standard for the evaluation of causal discovery methods and can serve as an accessible entry point for practitioners interested in the field, highlighting the empirical implications of different algorithm choices.

Tightening Bounds on Probabilities of Causation By Merging Datasets

Probabilities of Causation (PoC) play a fundamental role in decision-making in law, health care and public policy. Nevertheless, their point identification is challenging, requiring strong assumptions, in the absence of which only bounds can be derived. Existing work to further tighten these bounds by leveraging extra information either provides numerical bounds, symbolic bounds for fixed dimensionality, or requires access to multiple datasets that contain the same treatment and outcome variables. However, in many clinical, epidemiological and public policy applications, there exist external datasets that examine the effect of different treatments on the same outcome variable, or study the association between covariates and the outcome variable. These external datasets cannot be used in conjunction with the aforementioned bounds, since the former may entail different treatment assignment mechanisms, or even obey different causal structures. Here, we provide symbolic bounds on the PoC for this challenging scenario. We focus on combining either two randomized experiments studying different treatments, or a randomized experiment and an observational study, assuming causal sufficiency. Our symbolic bounds work for arbitrary dimensionality of covariates and treatment, and we discuss the conditions under which these bounds are tighter than existing bounds in literature. Finally, our bounds parameterize the difference in treatment assignment mechanism across datasets, allowing the mechanisms to vary across datasets while still allowing causal information to be transferred from the external dataset to the target dataset.

Beyond Single-Feature Importance with ICECREAM

Which set of features was responsible for a certain output of a machine learning model? Which components caused the failure of a cloud computing application? These are just two examples of questions we are addressing in this work by Identifying Coalition-based Explanations for Common and Rare Events in Any Model (ICECREAM). Specifically, we propose an information-theoretic quantitative measure for the influence of a coalition of variables on the distribution of a target variable. This allows us to identify which set of factors is essential to obtain a certain outcome, as opposed to well-established explainability and causal contribution analysis methods which can assign contributions only to individual factors and rank them by their importance. In experiments with synthetic and real-world data, we show that ICECREAM outperforms state-of-the-art methods for explainability and root cause analysis, and achieves impressive accuracy in both tasks.

Self-Compatibility: Evaluating Causal Discovery without Ground Truth

As causal ground truth is incredibly rare, causal discovery algorithms are commonly only evaluated on simulated data. This is concerning, given that simulations reflect common preconceptions about generating processes regarding noise distributions, model classes, and more. In this work, we propose a novel method for falsifying the output of a causal discovery algorithm in the absence of ground truth. Our key insight is that while statistical learning seeks stability across subsets of data points, causal learning should seek stability across subsets of variables. Motivated by this insight, our method relies on a notion of compatibility between causal graphs learned on different subsets of variables. We prove that detecting incompatibilities can falsify wrongly inferred causal relations due to violation of assumptions or errors from finite sample effects. Although passing such compatibility tests is only a necessary criterion for good performance, we argue that it provides strong evidence for the causal models whenever compatibility entails strong implications for the joint distribution. We also demonstrate experimentally that detection of incompatibilities can aid in causal model selection.

Toward Falsifying Causal Graphs Using a Permutation-Based Test

Understanding the causal relationships among the variables of a system is paramount to explain and control its behaviour. Inferring the causal graph from observational data without interventions, however, requires a lot of strong assumptions that are not always realistic. Even for domain experts it can be challenging to express the causal graph. Therefore, metrics that quantitatively assess the goodness of a causal graph provide helpful checks before using it in downstream tasks. Existing metrics provide an absolute number of inconsistencies between the graph and the observed data, and without a baseline, practitioners are left to answer the hard question of how many such inconsistencies are acceptable or expected. Here, we propose a novel consistency metric by constructing a surrogate baseline through node permutations. By comparing the number of inconsistencies with those on the surrogate baseline, we derive an interpretable metric that captures whether the DAG fits significantly better than random. Evaluating on both simulated and real data sets from various domains, including biology and cloud monitoring, we demonstrate that the true DAG is not falsified by our metric, whereas the wrong graphs given by a hypothetical user are likely to be falsified.

Bounding probabilities of causation through the causal marginal problem

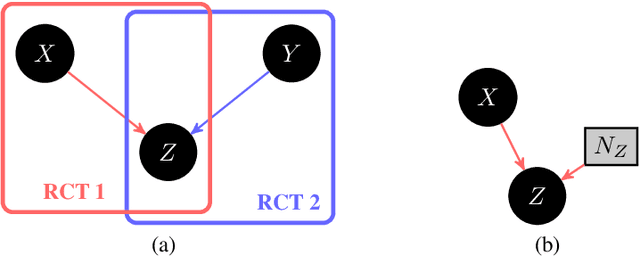
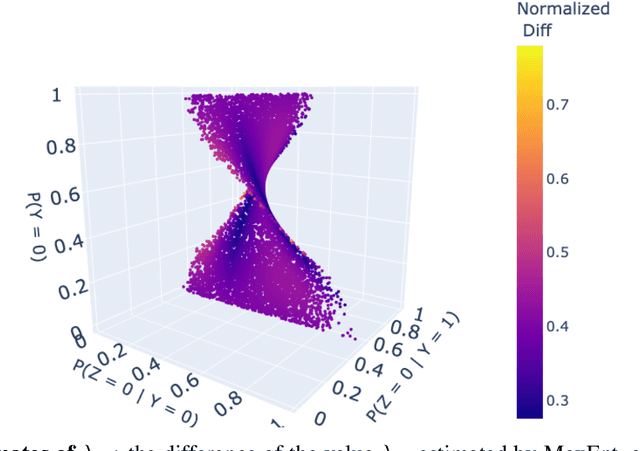
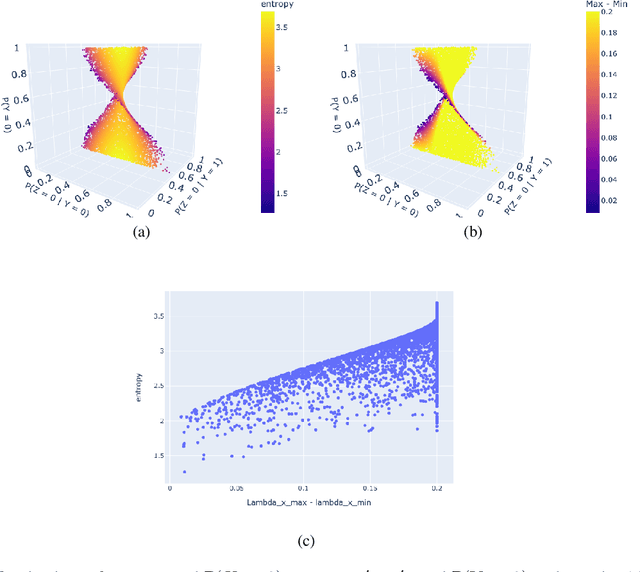
Probabilities of Causation play a fundamental role in decision making in law, health care and public policy. Nevertheless, their point identification is challenging, requiring strong assumptions such as monotonicity. In the absence of such assumptions, existing work requires multiple observations of datasets that contain the same treatment and outcome variables, in order to establish bounds on these probabilities. However, in many clinical trials and public policy evaluation cases, there exist independent datasets that examine the effect of a different treatment each on the same outcome variable. Here, we outline how to significantly tighten existing bounds on the probabilities of causation, by imposing counterfactual consistency between SCMs constructed from such independent datasets ('causal marginal problem'). Next, we describe a new information theoretic approach on falsification of counterfactual probabilities, using conditional mutual information to quantify counterfactual influence. The latter generalises to arbitrary discrete variables and number of treatments, and renders the causal marginal problem more interpretable. Since the question of 'tight enough' is left to the user, we provide an additional method of inference when the bounds are unsatisfactory: A maximum entropy based method that defines a metric for the space of plausible SCMs and proposes the entropy maximising SCM for inferring counterfactuals in the absence of more information.

DoWhy-GCM: An extension of DoWhy for causal inference in graphical causal models

We introduce DoWhy-GCM, an extension of the DoWhy Python library, that leverages graphical causal models. Unlike existing causality libraries, which mainly focus on effect estimation questions, with DoWhy-GCM, users can ask a wide range of additional causal questions, such as identifying the root causes of outliers and distributional changes, causal structure learning, attributing causal influences, and diagnosis of causal structures. To this end, DoWhy-GCM users first model cause-effect relations between variables in a system under study through a graphical causal model, fit the causal mechanisms of variables next, and then ask the causal question. All these steps take only a few lines of code in DoWhy-GCM. The library is available at https://github.com/py-why/dowhy.

Necessary and sufficient conditions for causal feature selection in time series with latent common causes

We study the identification of direct and indirect causes on time series and provide necessary and sufficient conditions in the presence of latent variables. Our theoretical results and estimation algorithms require two conditional independence tests for each observed candidate time series to determine whether or not it is a cause of an observed target time series. We provide experimental results in simulations, where the ground truth is known, as well as in real data. Our results show that our method leads to essentially no false positives and relatively low false negative rates, even in confounded environments with non-unique lag effects, outperforming the widely used Granger causality and two more methods.