On Different Notions of Redundancy in Conditional-Independence-Based Discovery of Graphical Models

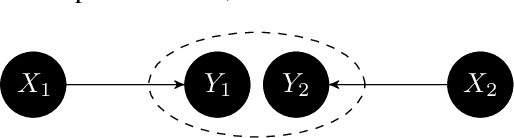
The goal of conditional-independence-based discovery of graphical models is to find a graph that represents the independence structure of variables in a given dataset. To learn such a representation, conditional-independence-based approaches conduct a set of statistical tests that suffices to identify the graphical representation under some assumptions on the underlying distribution of the data. In this work, we highlight that due to the conciseness of the graphical representation, there are often many tests that are not used in the construction of the graph. These redundant tests have the potential to detect or sometimes correct errors in the learned model. We show that not all tests contain this additional information and that such redundant tests have to be applied with care. Precisely, we argue that particularly those conditional (in)dependence statements are interesting that follow only from graphical assumptions but do not hold for every probability distribution.

Score matching through the roof: linear, nonlinear, and latent variables causal discovery

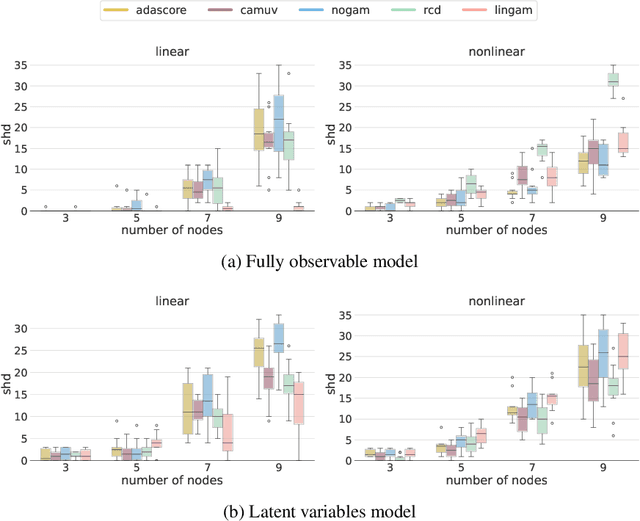
Causal discovery from observational data holds great promise, but existing methods rely on strong assumptions about the underlying causal structure, often requiring full observability of all relevant variables. We tackle these challenges by leveraging the score function $\nabla \log p(X)$ of observed variables for causal discovery and propose the following contributions. First, we generalize the existing results of identifiability with the score to additive noise models with minimal requirements on the causal mechanisms. Second, we establish conditions for inferring causal relations from the score even in the presence of hidden variables; this result is two-faced: we demonstrate the score's potential as an alternative to conditional independence tests to infer the equivalence class of causal graphs with hidden variables, and we provide the necessary conditions for identifying direct causes in latent variable models. Building on these insights, we propose a flexible algorithm for causal discovery across linear, nonlinear, and latent variable models, which we empirically validate.

Self-Compatibility: Evaluating Causal Discovery without Ground Truth

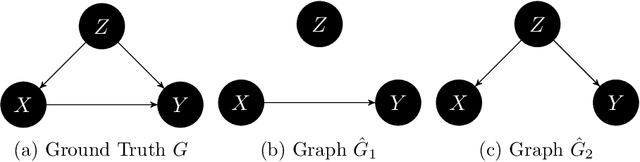
As causal ground truth is incredibly rare, causal discovery algorithms are commonly only evaluated on simulated data. This is concerning, given that simulations reflect common preconceptions about generating processes regarding noise distributions, model classes, and more. In this work, we propose a novel method for falsifying the output of a causal discovery algorithm in the absence of ground truth. Our key insight is that while statistical learning seeks stability across subsets of data points, causal learning should seek stability across subsets of variables. Motivated by this insight, our method relies on a notion of compatibility between causal graphs learned on different subsets of variables. We prove that detecting incompatibilities can falsify wrongly inferred causal relations due to violation of assumptions or errors from finite sample effects. Although passing such compatibility tests is only a necessary criterion for good performance, we argue that it provides strong evidence for the causal models whenever compatibility entails strong implications for the joint distribution. We also demonstrate experimentally that detection of incompatibilities can aid in causal model selection.

Reinterpreting causal discovery as the task of predicting unobserved joint statistics

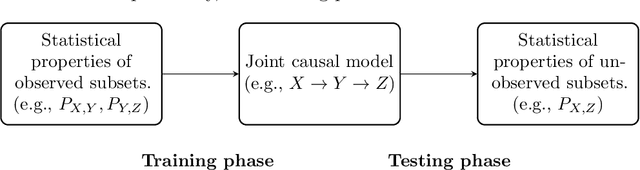
If $X,Y,Z$ denote sets of random variables, two different data sources may contain samples from $P_{X,Y}$ and $P_{Y,Z}$, respectively. We argue that causal discovery can help inferring properties of the `unobserved joint distributions' $P_{X,Y,Z}$ or $P_{X,Z}$. The properties may be conditional independences (as in `integrative causal inference') or also quantitative statements about dependences. More generally, we define a learning scenario where the input is a subset of variables and the label is some statistical property of that subset. Sets of jointly observed variables define the training points, while unobserved sets are possible test points. To solve this learning task, we infer, as an intermediate step, a causal model from the observations that then entails properties of unobserved sets. Accordingly, we can define the VC dimension of a class of causal models and derive generalization bounds for the predictions. Here, causal discovery becomes more modest and better accessible to empirical tests than usual: rather than trying to find a causal hypothesis that is `true' a causal hypothesis is {\it useful} whenever it correctly predicts statistical properties of unobserved joint distributions. This way, a sparse causal graph that omits weak influences may be more useful than a dense one (despite being less accurate) because it is able to reconstruct the full joint distribution from marginal distributions of smaller subsets. Within such a `pragmatic' application of causal discovery, some popular heuristic approaches become justified in retrospect. It is, for instance, allowed to infer DAGs from partial correlations instead of conditional independences if the DAGs are only used to predict partial correlations.