Score matching through the roof: linear, nonlinear, and latent variables causal discovery

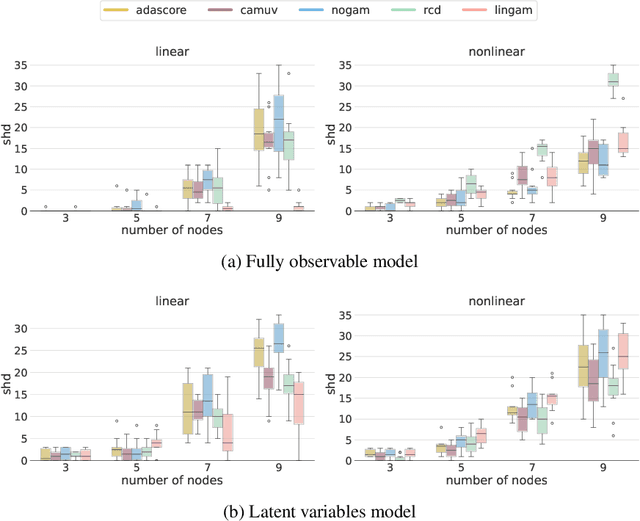
Causal discovery from observational data holds great promise, but existing methods rely on strong assumptions about the underlying causal structure, often requiring full observability of all relevant variables. We tackle these challenges by leveraging the score function $\nabla \log p(X)$ of observed variables for causal discovery and propose the following contributions. First, we generalize the existing results of identifiability with the score to additive noise models with minimal requirements on the causal mechanisms. Second, we establish conditions for inferring causal relations from the score even in the presence of hidden variables; this result is two-faced: we demonstrate the score's potential as an alternative to conditional independence tests to infer the equivalence class of causal graphs with hidden variables, and we provide the necessary conditions for identifying direct causes in latent variable models. Building on these insights, we propose a flexible algorithm for causal discovery across linear, nonlinear, and latent variable models, which we empirically validate.

Demystifying amortized causal discovery with transformers

Supervised learning approaches for causal discovery from observational data often achieve competitive performance despite seemingly avoiding explicit assumptions that traditional methods make for identifiability. In this work, we investigate CSIvA (Ke et al., 2023), a transformer-based model promising to train on synthetic data and transfer to real data. First, we bridge the gap with existing identifiability theory and show that constraints on the training data distribution implicitly define a prior on the test observations. Consistent with classical approaches, good performance is achieved when we have a good prior on the test data, and the underlying model is identifiable. At the same time, we find new trade-offs. Training on datasets generated from different classes of causal models, unambiguously identifiable in isolation, improves the test generalization. Performance is still guaranteed, as the ambiguous cases resulting from the mixture of identifiable causal models are unlikely to occur (which we formally prove). Overall, our study finds that amortized causal discovery still needs to obey identifiability theory, but it also differs from classical methods in how the assumptions are formulated, trading more reliance on assumptions on the noise type for fewer hypotheses on the mechanisms.

Shortcuts for causal discovery of nonlinear models by score matching

The use of simulated data in the field of causal discovery is ubiquitous due to the scarcity of annotated real data. Recently, Reisach et al., 2021 highlighted the emergence of patterns in simulated linear data, which displays increasing marginal variance in the casual direction. As an ablation in their experiments, Montagna et al., 2023 found that similar patterns may emerge in nonlinear models for the variance of the score vector $\nabla \log p_{\mathbf{X}}$, and introduced the ScoreSort algorithm. In this work, we formally define and characterize this score-sortability pattern of nonlinear additive noise models. We find that it defines a class of identifiable (bivariate) causal models overlapping with nonlinear additive noise models. We theoretically demonstrate the advantages of ScoreSort in terms of statistical efficiency compared to prior state-of-the-art score matching-based methods and empirically show the score-sortability of the most common synthetic benchmarks in the literature. Our findings remark (1) the lack of diversity in the data as an important limitation in the evaluation of nonlinear causal discovery approaches, (2) the importance of thoroughly testing different settings within a problem class, and (3) the importance of analyzing statistical properties in causal discovery, where research is often limited to defining identifiability conditions of the model.

Assumption violations in causal discovery and the robustness of score matching

When domain knowledge is limited and experimentation is restricted by ethical, financial, or time constraints, practitioners turn to observational causal discovery methods to recover the causal structure, exploiting the statistical properties of their data. Because causal discovery without further assumptions is an ill-posed problem, each algorithm comes with its own set of usually untestable assumptions, some of which are hard to meet in real datasets. Motivated by these considerations, this paper extensively benchmarks the empirical performance of recent causal discovery methods on observational i.i.d. data generated under different background conditions, allowing for violations of the critical assumptions required by each selected approach. Our experimental findings show that score matching-based methods demonstrate surprising performance in the false positive and false negative rate of the inferred graph in these challenging scenarios, and we provide theoretical insights into their performance. This work is also the first effort to benchmark the stability of causal discovery algorithms with respect to the values of their hyperparameters. Finally, we hope this paper will set a new standard for the evaluation of causal discovery methods and can serve as an accessible entry point for practitioners interested in the field, highlighting the empirical implications of different algorithm choices.

Scalable Causal Discovery with Score Matching

This paper demonstrates how to discover the whole causal graph from the second derivative of the log-likelihood in observational non-linear additive Gaussian noise models. Leveraging scalable machine learning approaches to approximate the score function $\nabla \log p(\mathbf{X})$, we extend the work of Rolland et al. (2022) that only recovers the topological order from the score and requires an expensive pruning step removing spurious edges among those admitted by the ordering. Our analysis leads to DAS (acronym for Discovery At Scale), a practical algorithm that reduces the complexity of the pruning by a factor proportional to the graph size. In practice, DAS achieves competitive accuracy with current state-of-the-art while being over an order of magnitude faster. Overall, our approach enables principled and scalable causal discovery, significantly lowering the compute bar.

Causal Discovery with Score Matching on Additive Models with Arbitrary Noise

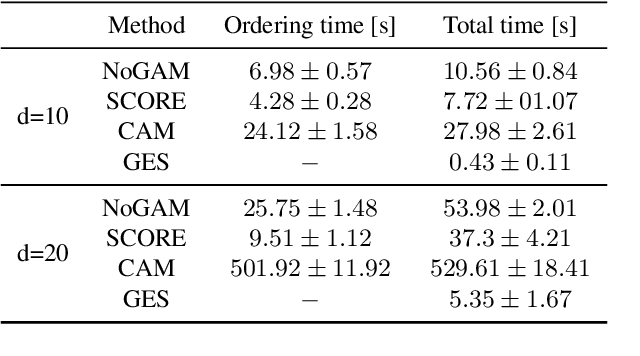
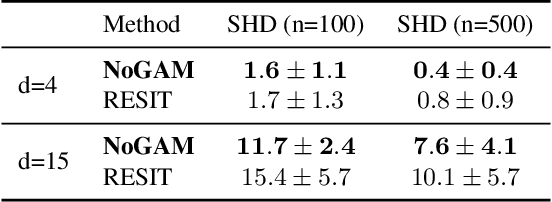
Causal discovery methods are intrinsically constrained by the set of assumptions needed to ensure structure identifiability. Moreover additional restrictions are often imposed in order to simplify the inference task: this is the case for the Gaussian noise assumption on additive non-linear models, which is common to many causal discovery approaches. In this paper we show the shortcomings of inference under this hypothesis, analyzing the risk of edge inversion under violation of Gaussianity of the noise terms. Then, we propose a novel method for inferring the topological ordering of the variables in the causal graph, from data generated according to an additive non-linear model with a generic noise distribution. This leads to NoGAM (Not only Gaussian Additive noise Models), a causal discovery algorithm with a minimal set of assumptions and state of the art performance, experimentally benchmarked on synthetic data.