Tightening Bounds on Probabilities of Causation By Merging Datasets

Probabilities of Causation (PoC) play a fundamental role in decision-making in law, health care and public policy. Nevertheless, their point identification is challenging, requiring strong assumptions, in the absence of which only bounds can be derived. Existing work to further tighten these bounds by leveraging extra information either provides numerical bounds, symbolic bounds for fixed dimensionality, or requires access to multiple datasets that contain the same treatment and outcome variables. However, in many clinical, epidemiological and public policy applications, there exist external datasets that examine the effect of different treatments on the same outcome variable, or study the association between covariates and the outcome variable. These external datasets cannot be used in conjunction with the aforementioned bounds, since the former may entail different treatment assignment mechanisms, or even obey different causal structures. Here, we provide symbolic bounds on the PoC for this challenging scenario. We focus on combining either two randomized experiments studying different treatments, or a randomized experiment and an observational study, assuming causal sufficiency. Our symbolic bounds work for arbitrary dimensionality of covariates and treatment, and we discuss the conditions under which these bounds are tighter than existing bounds in literature. Finally, our bounds parameterize the difference in treatment assignment mechanism across datasets, allowing the mechanisms to vary across datasets while still allowing causal information to be transferred from the external dataset to the target dataset.

Bounding probabilities of causation through the causal marginal problem

Probabilities of Causation play a fundamental role in decision making in law, health care and public policy. Nevertheless, their point identification is challenging, requiring strong assumptions such as monotonicity. In the absence of such assumptions, existing work requires multiple observations of datasets that contain the same treatment and outcome variables, in order to establish bounds on these probabilities. However, in many clinical trials and public policy evaluation cases, there exist independent datasets that examine the effect of a different treatment each on the same outcome variable. Here, we outline how to significantly tighten existing bounds on the probabilities of causation, by imposing counterfactual consistency between SCMs constructed from such independent datasets ('causal marginal problem'). Next, we describe a new information theoretic approach on falsification of counterfactual probabilities, using conditional mutual information to quantify counterfactual influence. The latter generalises to arbitrary discrete variables and number of treatments, and renders the causal marginal problem more interpretable. Since the question of 'tight enough' is left to the user, we provide an additional method of inference when the bounds are unsatisfactory: A maximum entropy based method that defines a metric for the space of plausible SCMs and proposes the entropy maximising SCM for inferring counterfactuals in the absence of more information.

Robustness in Deep Learning for Computer Vision: Mind the gap?

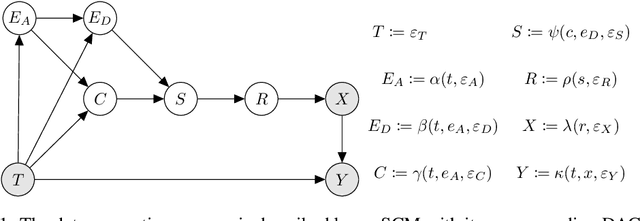
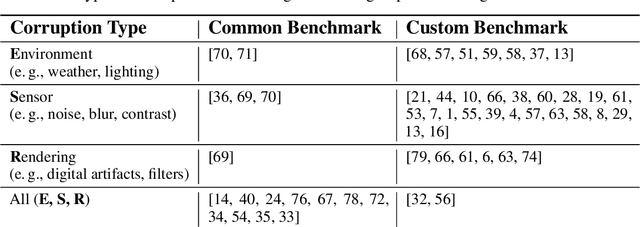
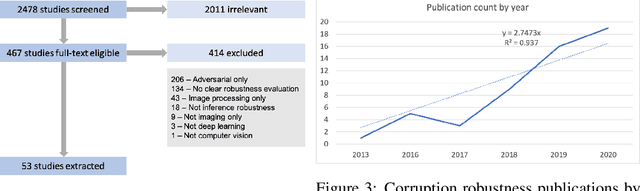
Deep neural networks for computer vision tasks are deployed in increasingly safety-critical and socially-impactful applications, motivating the need to close the gap in model performance under varied, naturally occurring imaging conditions. Robustness, ambiguously used in multiple contexts including adversarial machine learning, here then refers to preserving model performance under naturally-induced image corruptions or alterations. We perform a systematic review to identify, analyze, and summarize current definitions and progress towards non-adversarial robustness in deep learning for computer vision. We find that this area of research has received disproportionately little attention relative to adversarial machine learning, yet a significant robustness gap exists that often manifests in performance degradation similar in magnitude to adversarial conditions. To provide a more transparent definition of robustness across contexts, we introduce a structural causal model of the data generating process and interpret non-adversarial robustness as pertaining to a model's behavior on corrupted images which correspond to low-probability samples from the unaltered data distribution. We then identify key architecture-, data augmentation-, and optimization tactics for improving neural network robustness. This causal view of robustness reveals that common practices in the current literature, both in regards to robustness tactics and evaluations, correspond to causal concepts, such as soft interventions resulting in a counterfactually-altered distribution of imaging conditions. Through our findings and analysis, we offer perspectives on how future research may mind this evident and significant non-adversarial robustness gap.

Multiply Robust Causal Mediation Analysis with Continuous Treatments

In many applications, researchers are interested in the direct and indirect causal effects of an intervention on an outcome of interest. Mediation analysis offers a rigorous framework for the identification and estimation of such causal quantities. In the case of binary treatment, efficient estimators for the direct and indirect effects are derived by Tchetgen Tchetgen and Shpitser (2012). These estimators are based on influence functions and possess desirable multiple robustness properties. However, they are not readily applicable when treatments are continuous, which is the case in several settings, such as drug dosage in medical applications. In this work, we extend the influence function-based estimator of Tchetgen Tchetgen and Shpitser (2012) to deal with continuous treatments by utilizing a kernel smoothing approach. We first demonstrate that our proposed estimator preserves the multiple robustness property of the estimator in Tchetgen Tchetgen and Shpitser (2012). Then we show that under certain mild regularity conditions, our estimator is asymptotically normal. Our estimation scheme allows for high-dimensional nuisance parameters that can be estimated at slower rates than the target parameter. Additionally, we utilize cross-fitting, which allows for weaker smoothness requirements for the nuisance functions.

A Semiparametric Approach to Interpretable Machine Learning

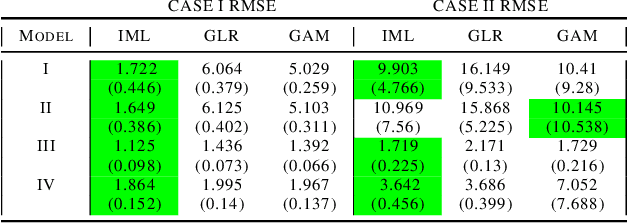
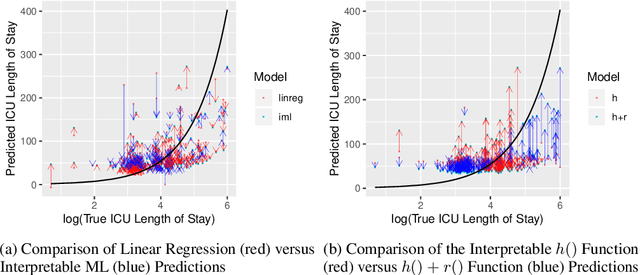
Black box models in machine learning have demonstrated excellent predictive performance in complex problems and high-dimensional settings. However, their lack of transparency and interpretability restrict the applicability of such models in critical decision-making processes. In order to combat this shortcoming, we propose a novel approach to trading off interpretability and performance in prediction models using ideas from semiparametric statistics, allowing us to combine the interpretability of parametric regression models with performance of nonparametric methods. We achieve this by utilizing a two-piece model: the first piece is interpretable and parametric, to which a second, uninterpretable residual piece is added. The performance of the overall model is optimized using methods from the sufficient dimension reduction literature. Influence function based estimators are derived and shown to be doubly robust. This allows for use of approaches such as double Machine Learning in estimating our model parameters. We illustrate the utility of our approach via simulation studies and a data application based on predicting the length of stay in the intensive care unit among surgery patients.

Explaining The Behavior Of Black-Box Prediction Algorithms With Causal Learning

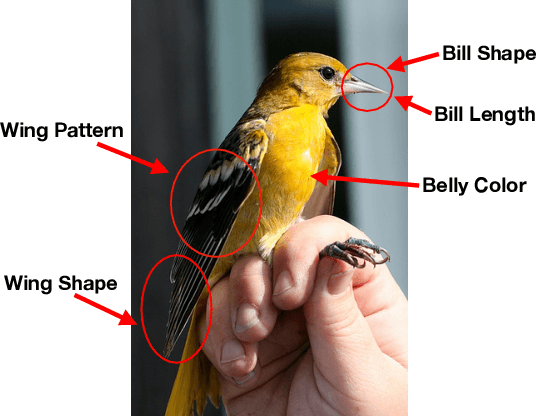
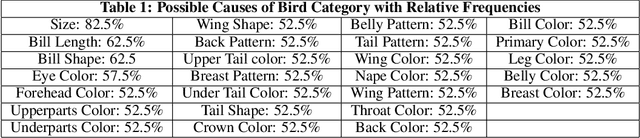
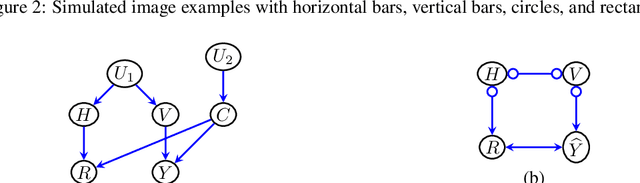
We propose to explain the behavior of black-box prediction methods (e.g., deep neural networks trained on image pixel data) using causal graphical models. Specifically, we explore learning the structure of a causal graph where the nodes represent prediction outcomes along with a set of macro-level "interpretable" features, while allowing for arbitrary unmeasured confounding among these variables. The resulting graph may indicate which of the interpretable features, if any, are possible causes of the prediction outcome and which may be merely associated with prediction outcomes due to confounding. The approach is motivated by a counterfactual theory of causal explanation wherein good explanations point to factors which are "difference-makers" in an interventionist sense. The resulting analysis may be useful in algorithm auditing and evaluation, by identifying features which make a causal difference to the algorithm's output.