Differentiable Causal Discovery Under Unmeasured Confounding

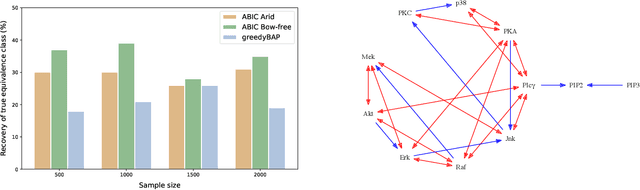
The data drawn from biological, economic, and social systems are often confounded due to the presence of unmeasured variables. Prior work in causal discovery has focused on discrete search procedures for selecting acyclic directed mixed graphs (ADMGs), specifically ancestral ADMGs, that encode ordinary conditional independence constraints among the observed variables of the system. However, confounded systems also exhibit more general equality restrictions that cannot be represented via these graphs, placing a limit on the kinds of structures that can be learned using ancestral ADMGs. In this work, we derive differentiable algebraic constraints that fully characterize the space of ancestral ADMGs, as well as more general classes of ADMGs, arid ADMGs and bow-free ADMGs, that capture all equality restrictions on the observed variables. We use these constraints to cast causal discovery as a continuous optimization problem and design differentiable procedures to find the best fitting ADMG when the data comes from a confounded linear system of equations with correlated errors. We demonstrate the efficacy of our method through simulations and application to a protein expression dataset.

Explaining The Behavior Of Black-Box Prediction Algorithms With Causal Learning

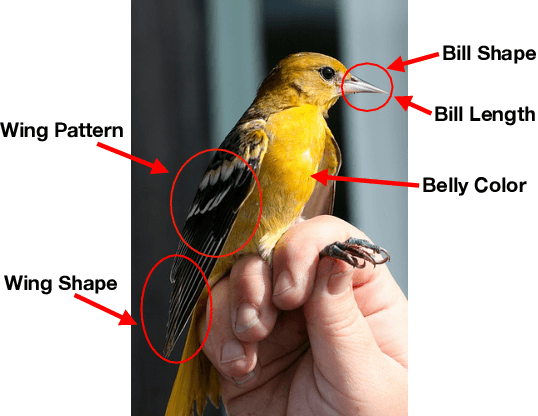
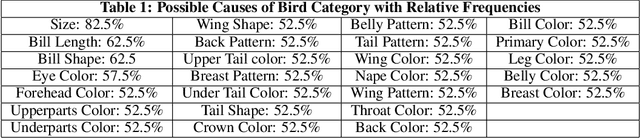
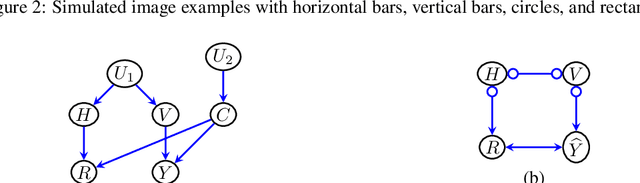
We propose to explain the behavior of black-box prediction methods (e.g., deep neural networks trained on image pixel data) using causal graphical models. Specifically, we explore learning the structure of a causal graph where the nodes represent prediction outcomes along with a set of macro-level "interpretable" features, while allowing for arbitrary unmeasured confounding among these variables. The resulting graph may indicate which of the interpretable features, if any, are possible causes of the prediction outcome and which may be merely associated with prediction outcomes due to confounding. The approach is motivated by a counterfactual theory of causal explanation wherein good explanations point to factors which are "difference-makers" in an interventionist sense. The resulting analysis may be useful in algorithm auditing and evaluation, by identifying features which make a causal difference to the algorithm's output.

Optimal Training of Fair Predictive Models

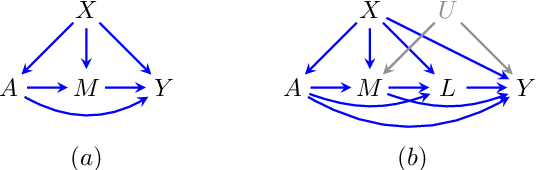
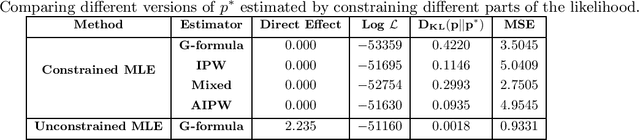
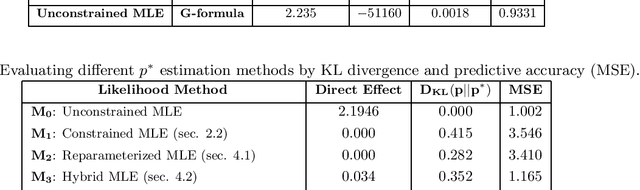
Recently there has been sustained interest in modifying prediction algorithms to satisfy fairness constraints. These constraints are typically complex nonlinear functionals of the observed data distribution. Focusing on the causal constraints proposed by Nabi and Shpitser (2018), we introduce new theoretical results and optimization techniques to make model training easier and more accurate. Specifically, we show how to reparameterize the observed data likelihood such that fairness constraints correspond directly to parameters that appear in the likelihood, transforming a complex constrained optimization objective into a simple optimization problem with box constraints. We also exploit methods from empirical likelihood theory in statistics to improve predictive performance, without requiring parametric models for high-dimensional feature vectors.

Causal Inference Under Interference And Network Uncertainty

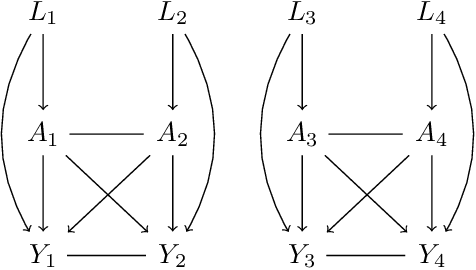
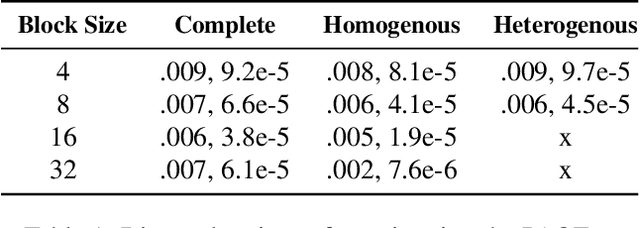
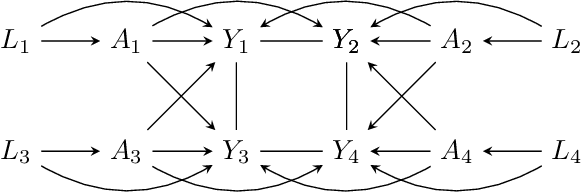
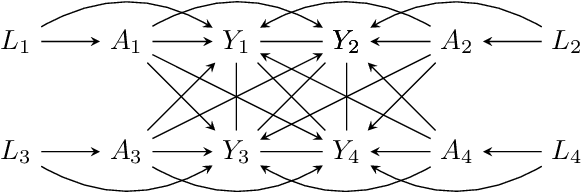
Classical causal and statistical inference methods typically assume the observed data consists of independent realizations. However, in many applications this assumption is inappropriate due to a network of dependences between units in the data. Methods for estimating causal effects have been developed in the setting where the structure of dependence between units is known exactly, but in practice there is often substantial uncertainty about the precise network structure. This is true, for example, in trial data drawn from vulnerable communities where social ties are difficult to query directly. In this paper we combine techniques from the structure learning and interference literatures in causal inference, proposing a general method for estimating causal effects under data dependence when the structure of this dependence is not known a priori. We demonstrate the utility of our method on synthetic datasets which exhibit network dependence.

Learning Optimal Fair Policies

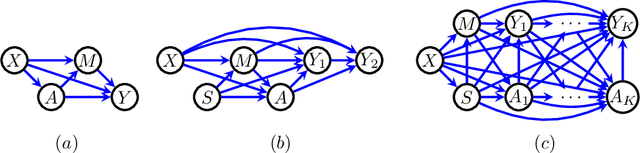
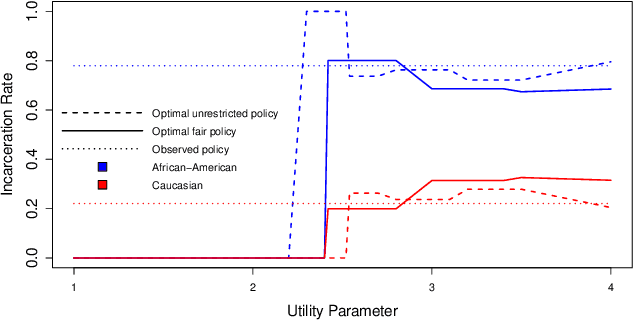
We consider the problem of learning optimal policies from observational data in a way that satisfies certain fairness criteria. The issue of fairness arises where some covariates used in decision making are sensitive features, or are correlated with sensitive features. (Nabi and Shpitser 2018) formalized fairness in the context of regression problems as constraining the causal effects of sensitive features along certain disallowed causal pathways. The existence of these causal effects may be called retrospective unfairness in the sense of already being present in the data before analysis begins, and may be due to discriminatory practices or the biased way in which variables are defined or recorded. In the context of learning policies, what we call prospective bias, i.e., the inappropriate dependence of learned policies on sensitive features, is also possible. In this paper, we use methods from causal and semiparametric inference to learn optimal policies in a way that addresses both retrospective bias in the data, and prospective bias due to the policy. In addition, our methods appropriately address statistical bias due to model misspecification and confounding bias, which are important in the estimation of path-specific causal effects from observational data. We apply our methods to both synthetic data and real criminal justice data.

Comparing the Performance of Graphical Structure Learning Algorithms with TETRAD

In this report we describe a tool for comparing the performance of causal structure learning algorithms implemented in the TETRAD freeware suite of causal analysis methods. Currently the tool is available as package in the TETRAD source code (written in Java), which can be loaded up in an Integrated Development Environment (IDE) such as IntelliJ IDEA. Simulations can be done varying the number of runs, sample sizes, and data modalities. Performance on this simulated data can then be compared for a number of algorithms, with parameters varied and with performance statistics as selected, producing a publishable report. The order of the algorithms in the output can be adjusted to the user's preference using a utility function over the statistics. Data sets from simulation can be saved along with their graphs to a file and loaded back in for further analysis, or used for analysis by other tools. The package presented here may also be used to compare structure learning methods across platforms and programming languages, i.e., to compare algorithms implemented in TETRAD with those implemented in MATLAB or R.