Choosing DAG Models Using Markov and Minimal Edge Count in the Absence of Ground Truth

We give a novel nonparametric pointwise consistent statistical test (the Markov Checker) of the Markov condition for directed acyclic graph (DAG) or completed partially directed acyclic graph (CPDAG) models given a dataset. We also introduce the Cross-Algorithm Frugality Search (CAFS) for rejecting DAG models that either do not pass the Markov Checker test or that are not edge minimal. Edge minimality has been used previously by Raskutti and Uhler as a nonparametric simplicity criterion, though CAFS readily generalizes to other simplicity conditions. Reference to the ground truth is not necessary for CAFS, so it is useful for finding causal structure learning algorithms and tuning parameter settings that output causal models that are approximately true from a given data set. We provide a software tool for this analysis that is suitable for even quite large or dense models, provided a suitably fast pointwise consistent test of conditional independence is available. In addition, we show in simulation that the CAFS procedure can pick approximately correct models without knowing the ground truth.

Py-Tetrad and RPy-Tetrad: A New Python Interface with R Support for Tetrad Causal Search

We give novel Python and R interfaces for the (Java) Tetrad project for causal modeling, search, and estimation. The Tetrad project is a mainstay in the literature, having been under consistent development for over 30 years. Some of its algorithms are now classics, like PC and FCI; others are recent developments. It is increasingly the case, however, that researchers need to access the underlying Java code from Python or R. Existing methods for doing this are inadequate. We provide new, up-to-date methods using the JPype Python-Java interface and the Reticulate Python-R interface, directly solving these issues. With the addition of some simple tools and the provision of working examples for both Python and R, using JPype and Reticulate to interface Python and R with Tetrad is straightforward and intuitive.

Improving Accuracy of Permutation DAG Search using Best Order Score Search

The Sparsest Permutation (SP) algorithm is accurate but limited to about 9 variables in practice; the Greedy Sparest Permutation (GSP) algorithm is faster but less weak theoretically. A compromise can be given, the Best Order Score Search, which gives results as accurate as SP but for much larger and denser graphs. BOSS (Best Order Score Search) is more accurate for two reason: (a) It assumes the "brute faithfuness" assumption, which is weaker than faithfulness, and (b) it uses a different traversal of permutations than the depth first traversal used by GSP, obtained by taking each variable in turn and moving it to the position in the permutation that optimizes the model score. Results are given comparing BOSS to several related papers in the literature in terms of performance, for linear, Gaussian data. In all cases, with the proper parameter settings, accuracy of BOSS is lifted considerably with respect to competing approaches. In configurations tested, models with 60 variables are feasible with large samples out to about an average degree of 12 in reasonable time, with near-perfect accuracy, and sparse models with an average degree of 4 are feasible out to about 300 variables on a laptop, again with near-perfect accuracy. Mixed continuous discrete and all-discrete datasets were also tested. The mixed data analysis showed advantage for BOSS over GES more apparent at higher depths with the same score; the discrete data analysis showed a very small advantage for BOSS over GES with the same score, perhaps not enough to prefer it.

Identification of Effective Connectivity Subregions

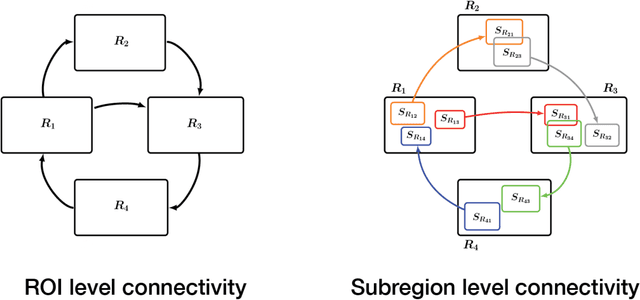
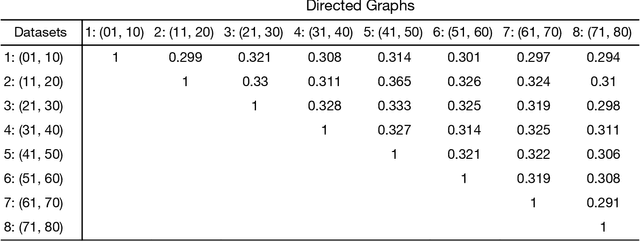
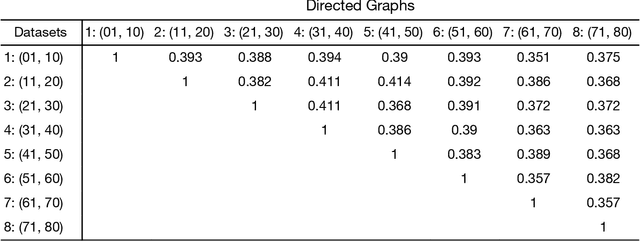
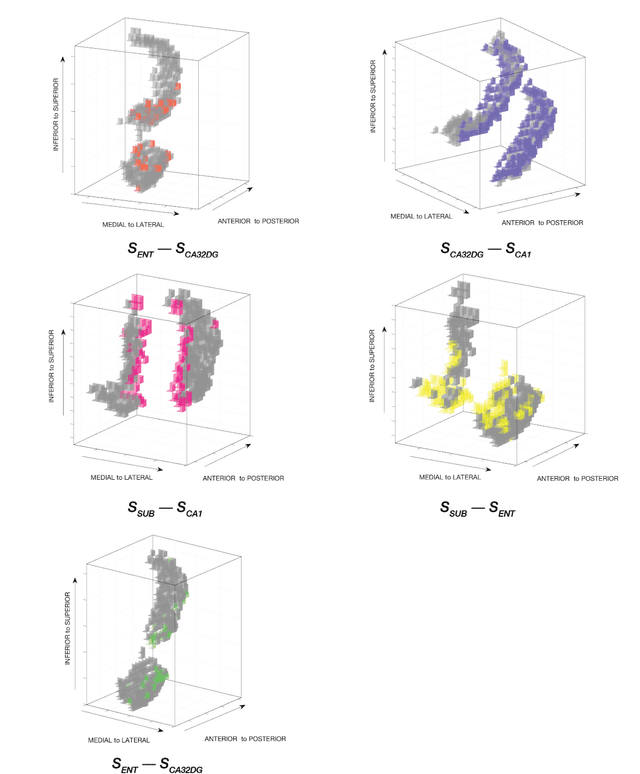
Standard fMRI connectivity analyses depend on aggregating the time series of individual voxels within regions of interest (ROIs). In certain cases, this spatial aggregation implies a loss of valuable functional and anatomical information about smaller subsets of voxels that drive the ROI level connectivity. We use two recently published graphical search methods to identify subsets of voxels that are highly responsible for the connectivity between larger ROIs. To illustrate the procedure, we apply both methods to longitudinal high-resolution resting state fMRI data from regions in the medial temporal lobe from a single individual. Both methods recovered similar subsets of voxels within larger ROIs of entorhinal cortex and hippocampus subfields that also show spatial consistency across different scanning sessions and across hemispheres. In contrast to standard functional connectivity methods, both algorithms applied here are robust against false positive connections produced by common causes and indirect paths (in contrast to Pearson's correlation) and common effect conditioning (in contrast to partial correlation based approaches). These algorithms allow for identification of subregions of voxels driving the connectivity between regions of interest, recovering valuable anatomical and functional information that is lost when ROIs are aggregated. Both methods are specially suited for voxelwise connectivity research, given their running times and scalability to big data problems.

Comparing the Performance of Graphical Structure Learning Algorithms with TETRAD

In this report we describe a tool for comparing the performance of causal structure learning algorithms implemented in the TETRAD freeware suite of causal analysis methods. Currently the tool is available as package in the TETRAD source code (written in Java), which can be loaded up in an Integrated Development Environment (IDE) such as IntelliJ IDEA. Simulations can be done varying the number of runs, sample sizes, and data modalities. Performance on this simulated data can then be compared for a number of algorithms, with parameters varied and with performance statistics as selected, producing a publishable report. The order of the algorithms in the output can be adjusted to the user's preference using a utility function over the statistics. Data sets from simulation can be saved along with their graphs to a file and loaded back in for further analysis, or used for analysis by other tools. The package presented here may also be used to compare structure learning methods across platforms and programming languages, i.e., to compare algorithms implemented in TETRAD with those implemented in MATLAB or R.

A Comparison of Public Causal Search Packages on Linear, Gaussian Data with No Latent Variables

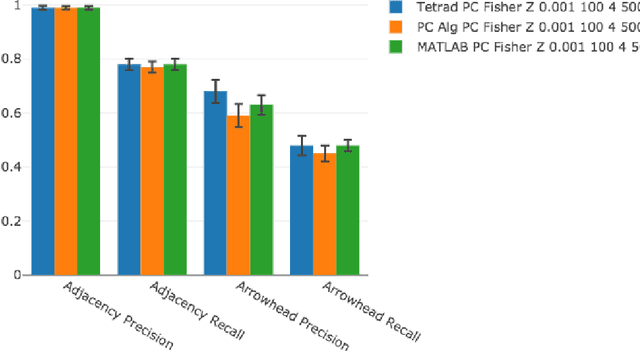
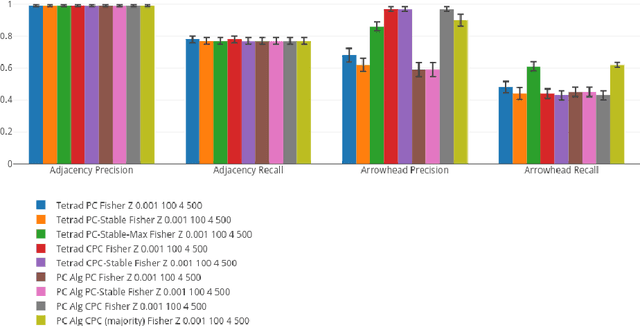
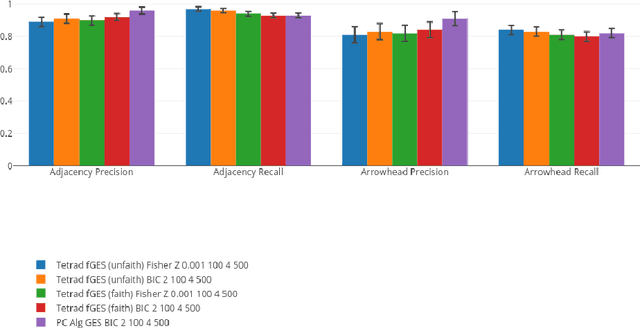
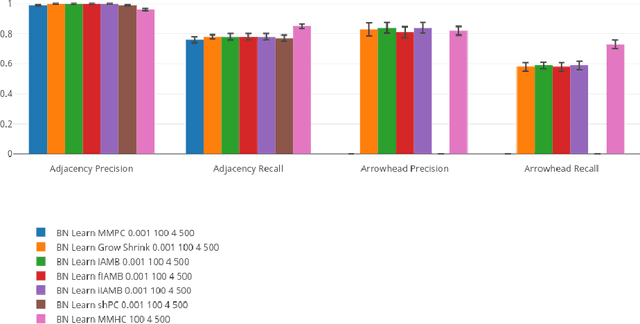
We compare Tetrad (Java) algorithms to the other public software packages BNT (Bayes Net Toolbox, Matlab), pcalg (R), bnlearn (R) on the \vanilla" task of recovering DAG structure to the extent possible from data generated recursively from linear, Gaussian structure equation models (SEMs) with no latent variables, for random graphs, with no additional knowledge of variable order or adjacency structure, and without additional specification of intervention information. Each one of the above packages offers at least one implementation suitable to this purpose. We compare them on adjacency and orientation accuracy as well as time performance, for fixed datasets. We vary the number of variables, the number of samples, and the density of graph, for a total of 27 combinations, averaging all statistics over 10 runs, for a total of 270 datasets. All runs are carried out on the same machine and on their native platforms. An interactive visualization tool is provided for the reader who wishes to know more than can be documented explicitly in this report.

Mixed Graphical Models for Causal Analysis of Multi-modal Variables

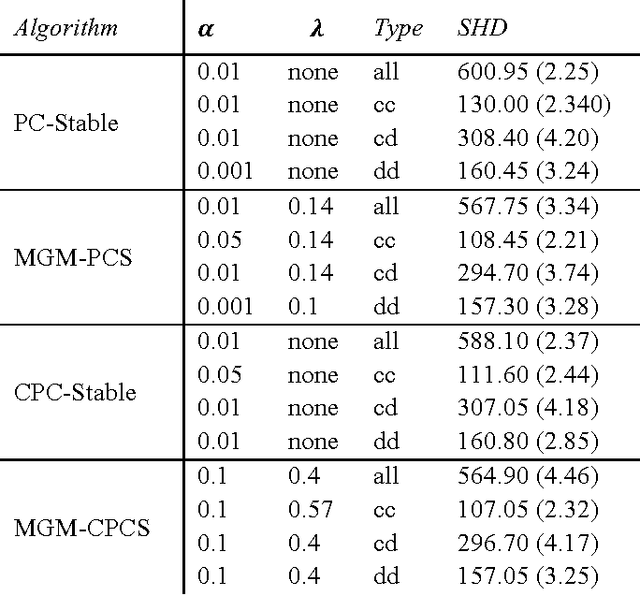
Graphical causal models are an important tool for knowledge discovery because they can represent both the causal relations between variables and the multivariate probability distributions over the data. Once learned, causal graphs can be used for classification, feature selection and hypothesis generation, while revealing the underlying causal network structure and thus allowing for arbitrary likelihood queries over the data. However, current algorithms for learning sparse directed graphs are generally designed to handle only one type of data (continuous-only or discrete-only), which limits their applicability to a large class of multi-modal biological datasets that include mixed type variables. To address this issue, we developed new methods that modify and combine existing methods for finding undirected graphs with methods for finding directed graphs. These hybrid methods are not only faster, but also perform better than the directed graph estimation methods alone for a variety of parameter settings and data set sizes. Here, we describe a new conditional independence test for learning directed graphs over mixed data types and we compare performances of different graph learning strategies on synthetic data.

Scaling up Greedy Causal Search for Continuous Variables

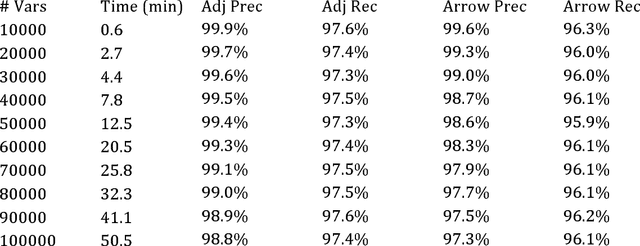
As standardly implemented in R or the Tetrad program, causal search algorithms used most widely or effectively by scientists have severe dimensionality constraints that make them inappropriate for big data problems without sacrificing accuracy. However, implementation improvements are possible. We explore optimizations for the Greedy Equivalence Search that allow search on 50,000-variable problems in 13 minutes for sparse models with 1000 samples on a four-processor, 16G laptop computer. We finish a problem with 1000 samples on 1,000,000 variables in 18 hours for sparse models on a supercomputer node at the Pittsburgh Supercomputing Center with 40 processors and 384 G RAM. The same algorithm can be applied to discrete data, with a slower discrete score, though the discrete implementation currently does not scale as well in our experiments; we have managed to scale up to about 10,000 variables in sparse models with 1000 samples.

Effects of Nonparanormal Transform on PC and GES Search Accuracies

Liu, et al., 2009 developed a transformation of a class of non-Gaussian univariate distributions into Gaussian distributions. Liu and collaborators (2012) subsequently applied the transform to search for graphical causal models for a number of empirical data sets. To our knowledge, there has been no published investigation by simulation of the conditions under which the transform aids, or harms, standard graphical model search procedures. We consider here how the transform affects the performance of two search algorithms in particular, PC (Spirtes et al., 2000; Meek 1995) and GES (Meek 1997; Chickering 2002). We find that the transform is harmless but ineffective for most cases but quite effective in very special cases for GES, namely, for moderate non-Gaussianity and moderate non-linearity. For strong-linearity, another algorithm, PC-GES (a combination of PC with GES), is equally effective.

A Scalable Conditional Independence Test for Nonlinear, Non-Gaussian Data

Many relations of scientific interest are nonlinear, and even in linear systems distributions are often non-Gaussian, for example in fMRI BOLD data. A class of search procedures for causal relations in high dimensional data relies on sample derived conditional independence decisions. The most common applications rely on Gaussian tests that can be systematically erroneous in nonlinear non-Gaussian cases. Recent work (Gretton et al. (2009), Tillman et al. (2009), Zhang et al. (2011)) has proposed conditional independence tests using Reproducing Kernel Hilbert Spaces (RKHS). Among these, perhaps the most efficient has been KCI (Kernel Conditional Independence, Zhang et al. (2011)), with computational requirements that grow effectively at least as O(N3), placing it out of range of large sample size analysis, and restricting its applicability to high dimensional data sets. We propose a class of O(N2) tests using conditional correlation independence (CCI) that require a few seconds on a standard workstation for tests that require tens of minutes to hours for the KCI method, depending on degree of parallelization, with similar accuracy. For accuracy on difficult nonlinear, non-Gaussian data sets, we also compare a recent test due to Harris & Drton (2012), applicable to nonlinear, non-Gaussian distributions in the Gaussian copula, as well as to partial correlation, a linear Gaussian test.